
Question Number 66228 by Rio Michael last updated on 11/Aug/19
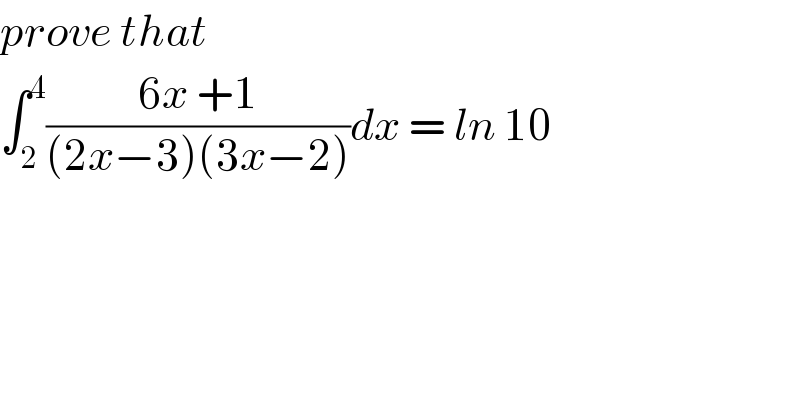
$${prove}\:{that}\: \\ $$$$\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\mathrm{6}{x}\:+\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{3}{x}−\mathrm{2}\right)}{dx}\:=\:{ln}\:\mathrm{10} \\ $$
Commented by Prithwish sen last updated on 11/Aug/19
![((6x+1)/((2x−3)(3x−2))) = (A/(2x−3)) + (B/(3x−2)) 6x+1 = A(3x−2) + B(2x−3) putting x = (2/3) we get 5 = B((4/3) −3)⇒B = −3 putting x = (3/2) we get 10=A((9/2) −2)⇒B=4 ∫_2 ^4 ((6x+1 )/((2x−3)(3x−2))) dx = ∫_2 ^4 [(4/(2x−3)) − (3/(3x−2))]dx =[ 2ln∣2x−3∣−ln∣3x−2∣]_2 ^4 =2ln5−ln10+1n4 =ln((25×4)/(10)) = ln10 proved.](Q66229.png)
$$\frac{\mathrm{6x}+\mathrm{1}}{\left(\mathrm{2x}−\mathrm{3}\right)\left(\mathrm{3x}−\mathrm{2}\right)}\:=\:\frac{\mathrm{A}}{\mathrm{2x}−\mathrm{3}}\:+\:\frac{\mathrm{B}}{\mathrm{3x}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{6x}+\mathrm{1}\:=\:\mathrm{A}\left(\mathrm{3x}−\mathrm{2}\right)\:+\:\mathrm{B}\left(\mathrm{2x}−\mathrm{3}\right) \\ $$$$\mathrm{putting}\:\:\mathrm{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{5}\:=\:\mathrm{B}\left(\frac{\mathrm{4}}{\mathrm{3}}\:−\mathrm{3}\right)\Rightarrow\mathrm{B}\:=\:−\mathrm{3} \\ $$$$\mathrm{putting}\:\mathrm{x}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{10}=\mathrm{A}\left(\frac{\mathrm{9}}{\mathrm{2}}\:−\mathrm{2}\right)\Rightarrow\mathrm{B}=\mathrm{4} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\mathrm{6x}+\mathrm{1}\:}{\left(\mathrm{2x}−\mathrm{3}\right)\left(\mathrm{3x}−\mathrm{2}\right)}\:\mathrm{dx}\:=\:\int_{\mathrm{2}} ^{\mathrm{4}} \left[\frac{\mathrm{4}}{\mathrm{2x}−\mathrm{3}}\:−\:\frac{\mathrm{3}}{\mathrm{3x}−\mathrm{2}}\right]\mathrm{dx} \\ $$$$=\left[\:\mathrm{2ln}\mid\mathrm{2x}−\mathrm{3}\mid−\mathrm{ln}\mid\mathrm{3x}−\mathrm{2}\mid\right]_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{2ln5}−\mathrm{ln10}+\mathrm{1n4} \\ $$$$=\mathrm{ln}\frac{\mathrm{25}×\mathrm{4}}{\mathrm{10}}\:=\:\mathrm{ln10}\:\:\:\:\mathrm{proved}. \\ $$$$ \\ $$$$ \\ $$
Commented by Rio Michael last updated on 11/Aug/19

$${thanks} \\ $$
Commented by mathmax by abdo last updated on 11/Aug/19
![let I =∫_2 ^4 ((6x+1)/((2x−3)(3x−2)))dx let decompose F(x)=((6x+1)/((2x−3)(3x−2))) F(x)=(a/(2x−3))+(b/(3x−2)) a=lim_(x→(3/2)) (2x−3)F(x)=((10)/5)×2 =4 b=lim_(x→(2/3)) (3x−2)F(x)=(5/((4/3)−3)) =5×(−(3/5))=−3 ⇒ F(x)=(4/(2x−3))−(3/(3x−2)) ⇒∫_2 ^4 F(x)dx =∫_2 ^4 ((4/(2x−3))−(3/(3x−2)))dx =[2ln∣2x−3∣−ln∣3x−2∣]_2 ^4 =2ln(5)−ln(10)+ln(4) =2ln(5)−ln(2)−ln(5)+2ln(2) =ln(5)+ln(2)=ln(10)](Q66241.png)
$${let}\:{I}\:=\int_{\mathrm{2}} ^{\mathrm{4}} \:\frac{\mathrm{6}{x}+\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{3}{x}−\mathrm{2}\right)}{dx}\:\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{6}{x}+\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{3}\right)\left(\mathrm{3}{x}−\mathrm{2}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{\mathrm{2}{x}−\mathrm{3}}+\frac{{b}}{\mathrm{3}{x}−\mathrm{2}} \\ $$$${a}={lim}_{{x}\rightarrow\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{2}{x}−\mathrm{3}\right){F}\left({x}\right)=\frac{\mathrm{10}}{\mathrm{5}}×\mathrm{2}\:=\mathrm{4} \\ $$$${b}={lim}_{{x}\rightarrow\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{3}{x}−\mathrm{2}\right){F}\left({x}\right)=\frac{\mathrm{5}}{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{3}}\:=\mathrm{5}×\left(−\frac{\mathrm{3}}{\mathrm{5}}\right)=−\mathrm{3}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{4}}{\mathrm{2}{x}−\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{3}{x}−\mathrm{2}}\:\Rightarrow\int_{\mathrm{2}} ^{\mathrm{4}} \:{F}\left({x}\right){dx}\:=\int_{\mathrm{2}} ^{\mathrm{4}} \left(\frac{\mathrm{4}}{\mathrm{2}{x}−\mathrm{3}}−\frac{\mathrm{3}}{\mathrm{3}{x}−\mathrm{2}}\right){dx} \\ $$$$=\left[\mathrm{2}{ln}\mid\mathrm{2}{x}−\mathrm{3}\mid−{ln}\mid\mathrm{3}{x}−\mathrm{2}\mid\right]_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{2}{ln}\left(\mathrm{5}\right)−{ln}\left(\mathrm{10}\right)+{ln}\left(\mathrm{4}\right) \\ $$$$=\mathrm{2}{ln}\left(\mathrm{5}\right)−{ln}\left(\mathrm{2}\right)−{ln}\left(\mathrm{5}\right)+\mathrm{2}{ln}\left(\mathrm{2}\right)\:={ln}\left(\mathrm{5}\right)+{ln}\left(\mathrm{2}\right)={ln}\left(\mathrm{10}\right) \\ $$
