Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 66321 by mathmax by abdo last updated on 12/Aug/19

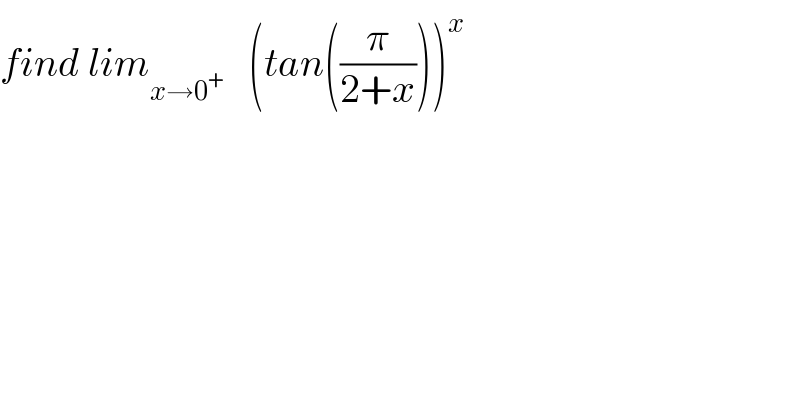
find lim_(x→0^+ ) (tan((π/(2+x))))^x

$${find}\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:\left({tan}\left(\frac{\pi}{\mathrm{2}+{x}}\right)\right)^{{x}} \\ $$

Commented by mathmax by abdo last updated on 24/Aug/19

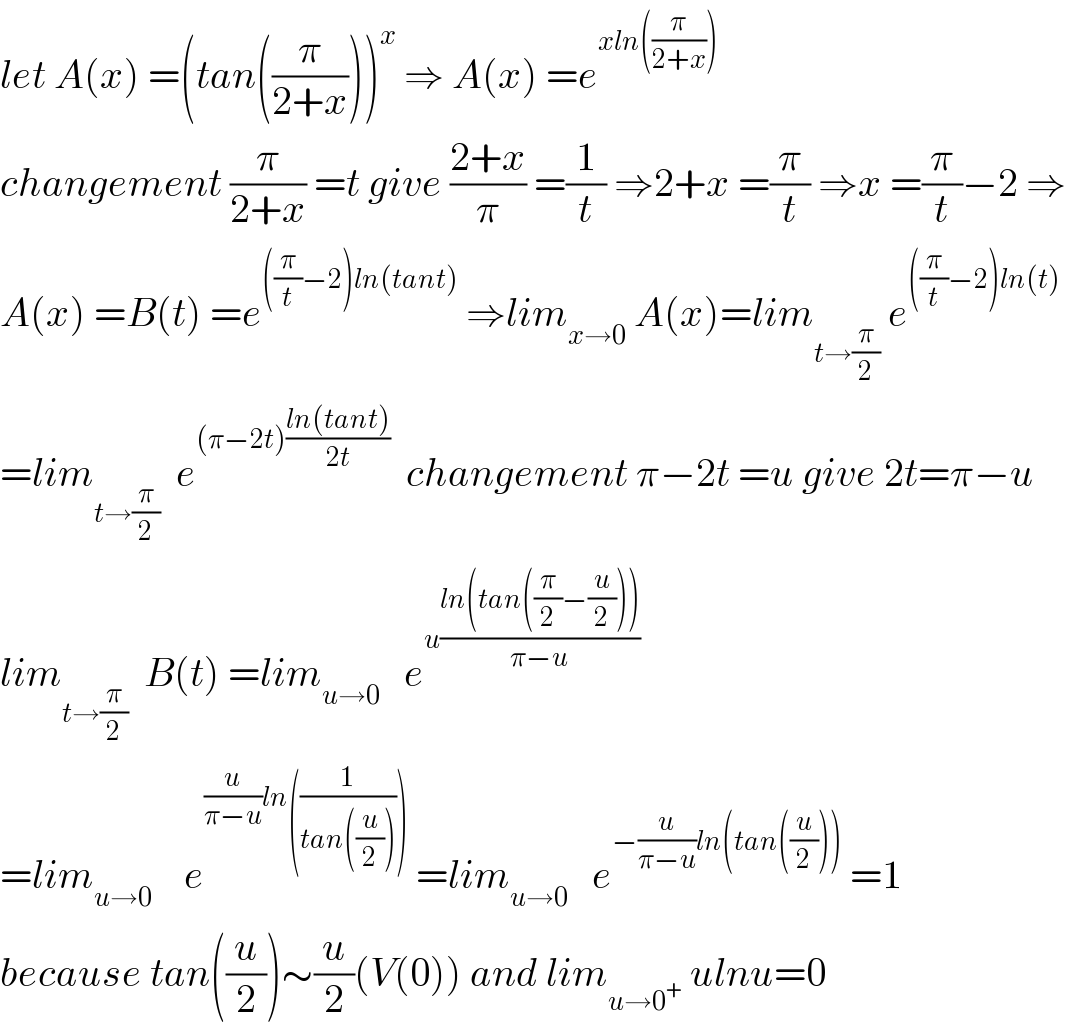
let A(x) =(tan((π/(2+x))))^x ⇒ A(x) =e^(xln((π/(2+x)))) changement (π/(2+x)) =t give ((2+x)/π) =(1/t) ⇒2+x =(π/t) ⇒x =(π/t)−2 ⇒ A(x) =B(t) =e^(((π/t)−2)ln(tant)) ⇒lim_(x→0) A(x)=lim_(t→(π/2)) e^(((π/t)−2)ln(t)) =lim_(t→(π/2)) e^((π−2t)((ln(tant))/(2t))) changement π−2t =u give 2t=π−u lim_(t→(π/2)) B(t) =lim_(u→0) e^(u((ln(tan((π/2)−(u/2))))/(π−u))) =lim_(u→0) e^((u/(π−u))ln((1/(tan((u/2)))))) =lim_(u→0) e^(−(u/(π−u))ln(tan((u/2)))) =1 because tan((u/2))∼(u/2)(V(0)) and lim_(u→0^+ ) ulnu=0

$${let}\:{A}\left({x}\right)\:=\left({tan}\left(\frac{\pi}{\mathrm{2}+{x}}\right)\right)^{{x}} \:\Rightarrow\:{A}\left({x}\right)\:={e}^{{xln}\left(\frac{\pi}{\mathrm{2}+{x}}\right)} \\ $$$${changement}\:\frac{\pi}{\mathrm{2}+{x}}\:={t}\:{give}\:\frac{\mathrm{2}+{x}}{\pi}\:=\frac{\mathrm{1}}{{t}}\:\Rightarrow\mathrm{2}+{x}\:=\frac{\pi}{{t}}\:\Rightarrow{x}\:=\frac{\pi}{{t}}−\mathrm{2}\:\Rightarrow \\ $$$${A}\left({x}\right)\:={B}\left({t}\right)\:={e}^{\left(\frac{\pi}{{t}}−\mathrm{2}\right){ln}\left({tant}\right)} \:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{A}\left({x}\right)={lim}_{{t}\rightarrow\frac{\pi}{\mathrm{2}}} \:{e}^{\left(\frac{\pi}{{t}}−\mathrm{2}\right){ln}\left({t}\right)} \\ $$$$={lim}_{{t}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:{e}^{\left(\pi−\mathrm{2}{t}\right)\frac{{ln}\left({tant}\right)}{\mathrm{2}{t}}} \:\:{changement}\:\pi−\mathrm{2}{t}\:={u}\:{give}\:\mathrm{2}{t}=\pi−{u} \\ $$$${lim}_{{t}\rightarrow\frac{\pi}{\mathrm{2}}} \:\:{B}\left({t}\right)\:={lim}_{{u}\rightarrow\mathrm{0}} \:\:\:{e}^{{u}\frac{{ln}\left({tan}\left(\frac{\pi}{\mathrm{2}}−\frac{{u}}{\mathrm{2}}\right)\right)}{\pi−{u}}} \\ $$$$={lim}_{{u}\rightarrow\mathrm{0}} \:\:\:\:{e}^{\frac{{u}}{\pi−{u}}{ln}\left(\frac{\mathrm{1}}{{tan}\left(\frac{{u}}{\mathrm{2}}\right)}\right)} \:={lim}_{{u}\rightarrow\mathrm{0}} \:\:\:{e}^{−\frac{{u}}{\pi−{u}}{ln}\left({tan}\left(\frac{{u}}{\mathrm{2}}\right)\right)} \:=\mathrm{1}\: \\ $$$${because}\:{tan}\left(\frac{{u}}{\mathrm{2}}\right)\sim\frac{{u}}{\mathrm{2}}\left({V}\left(\mathrm{0}\right)\right)\:{and}\:{lim}_{{u}\rightarrow\mathrm{0}^{+} } \:{ulnu}=\mathrm{0} \\ $$

Commented by mathmax by abdo last updated on 24/Aug/19

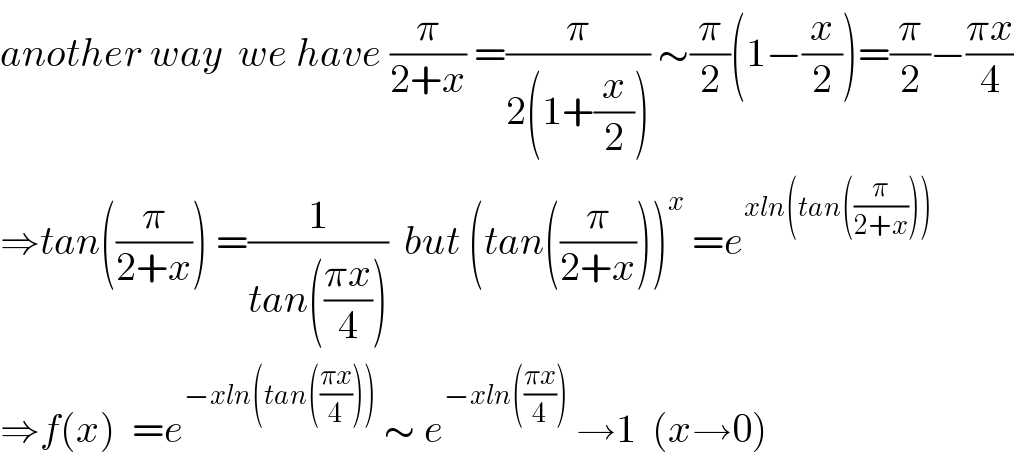
another way we have (π/(2+x)) =(π/(2(1+(x/2)))) ∼(π/2)(1−(x/2))=(π/2)−((πx)/4) ⇒tan((π/(2+x))) =(1/(tan(((πx)/4)))) but (tan((π/(2+x))))^x =e^(xln(tan((π/(2+x))))) ⇒f(x) =e^(−xln(tan(((πx)/4)))) ∼ e^(−xln(((πx)/4))) →1 (x→0)

$${another}\:{way}\:\:{we}\:{have}\:\frac{\pi}{\mathrm{2}+{x}}\:=\frac{\pi}{\mathrm{2}\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)}\:\sim\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{2}}−\frac{\pi{x}}{\mathrm{4}} \\ $$$$\Rightarrow{tan}\left(\frac{\pi}{\mathrm{2}+{x}}\right)\:=\frac{\mathrm{1}}{{tan}\left(\frac{\pi{x}}{\mathrm{4}}\right)}\:\:{but}\:\left({tan}\left(\frac{\pi}{\mathrm{2}+{x}}\right)\right)^{{x}} \:={e}^{{xln}\left({tan}\left(\frac{\pi}{\mathrm{2}+{x}}\right)\right)} \\ $$$$\Rightarrow{f}\left({x}\right)\:\:={e}^{−{xln}\left({tan}\left(\frac{\pi{x}}{\mathrm{4}}\right)\right)} \:\sim\:{e}^{−{xln}\left(\frac{\pi{x}}{\mathrm{4}}\right)} \:\rightarrow\mathrm{1}\:\:\left({x}\rightarrow\mathrm{0}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com