Question Number 66325 by mathmax by abdo last updated on 12/Aug/19
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{4}} {x}\:{sin}^{\mathrm{2}} {x}\:{dx} \\ $$
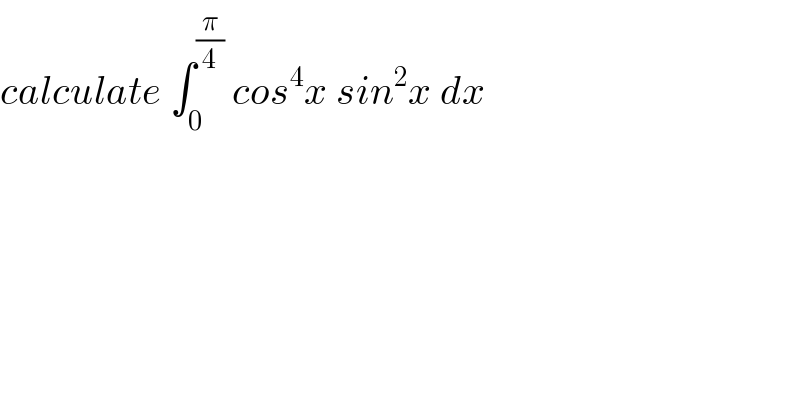
Commented by Prithwish sen last updated on 13/Aug/19
![(1/8)∫_0 ^(π/4) (cos2x+1)sin^2 2xdx=(1/8)∫_0 ^(π/4) cos2xsin^2 2xdx+(1/(16))∫_0 ^(π/4) (1−cos4x)dx =[((sin^3 2x)/(48)) +(x/(16)) −((sin4x)/(64))]_0 ^(π/4) = (1/(48)) + (π/(64 )) please check.](Q66364.png)
$$\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{cos2x}+\mathrm{1}\right)\mathrm{sin}^{\mathrm{2}} \mathrm{2xdx}=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{cos2xsin}^{\mathrm{2}} \mathrm{2xdx}+\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}−\mathrm{cos4x}\right)\mathrm{dx} \\ $$$$=\left[\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{2x}}{\mathrm{48}}\:+\frac{\mathrm{x}}{\mathrm{16}}\:−\frac{\mathrm{sin4x}}{\mathrm{64}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\:\frac{\mathrm{1}}{\mathrm{48}}\:+\:\frac{\pi}{\mathrm{64}\:}\:\:\mathrm{please}\:\mathrm{check}. \\ $$
Commented by mathmax by abdo last updated on 13/Aug/19
![let I =∫_0 ^(π/4) cos^4 x sin^2 x ⇒I =∫_0 ^(π/4) (((1+cos(2x))/2))^2 (((1−cos(2x))/2))dx =(1/8) ∫_0 ^(π/4) (1+2cos(2x)+((1+cos(4x))/2))(1−cos(2x)dx =(1/(16)) ∫_0 ^(π/4) (2+4cos(2x)+1+cos(4x))(1−cos(2x))dx =(1/(16)) ∫_0 ^(π/4) (3 +4cos(2x)+cos(4x))(1−cos(2x))dx 16 I =∫_0 ^(π/4) (3+4cos(2x)+cos(4x)−3cos(2x)−4cos^2 (2x)−cos(2x)cos(4x))dx =((3π)/4) + ∫_0 ^(π/4) cos(2x)dx +∫_0 ^(π/4) cos(4x)dx−4 ∫_0 ^(π/4) ((1+cos(4x))/2)dx −∫_0 ^(π/4) cos(2x)cos(4x)dx =((3π)/4) +(1/2)[sin(2x)]_0 ^(π/4) +(1/4)[sin(4x)]_0 ^(π/4) −(π/2) −(1/2)[sin(4x)]_0 ^(π/4) =((3π)/4)+(1/2)−(π/2) =(π/4) +(1/2)](Q66386.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}^{\mathrm{4}} {x}\:{sin}^{\mathrm{2}} {x}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right){dx}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{2}+\mathrm{4}{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{3}\:+\mathrm{4}{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{4}{x}\right)\right)\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$\mathrm{16}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{3}+\mathrm{4}{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{4}{x}\right)−\mathrm{3}{cos}\left(\mathrm{2}{x}\right)−\mathrm{4}{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{4}}\:+\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){dx}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{4}{x}\right){dx}−\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}{dx} \\ $$$$−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right){dx} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left[{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{4}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\left[{sin}\left(\mathrm{4}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 13/Aug/19
![error at final line 16 I =((3π)/4) +(1/2)−(π/2) −(1/2) ∫_0 ^(π/4) (cos(6x)+cos(2x))dx but ∫_0 ^(π/4) cos(6x)dx +∫_0 ^(π/4) cos(2x)dx =(1/6)[sin(6x)]_0 ^(π/4) +(1/2)[sin(2x)]_0 ^(π/4) =(1/6)sin(((3π)/2))+(1/2) =(1/2)−(1/6) ⇒ 16 I =(π/4) +(1/2)−(1/4) +(1/(12)) =(π/4) +(1/4)+(1/(12)) =(π/4) +(1/3) ⇒ I =(π/(64)) +(1/(48)) .](Q66388.png)
$${error}\:{at}\:{final}\:{line}\: \\ $$$$\mathrm{16}\:{I}\:=\frac{\mathrm{3}\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\left({cos}\left(\mathrm{6}{x}\right)+{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{6}{x}\right){dx}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{cos}\left(\mathrm{2}{x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{6}}\left[{sin}\left(\mathrm{6}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:+\frac{\mathrm{1}}{\mathrm{2}}\left[{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{16}\:{I}\:=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{12}}\:=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{12}}\:=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{\mathrm{64}}\:+\frac{\mathrm{1}}{\mathrm{48}}\:. \\ $$