
Question and Answers Forum
Question Number 66346 by mathmax by abdo last updated on 12/Aug/19
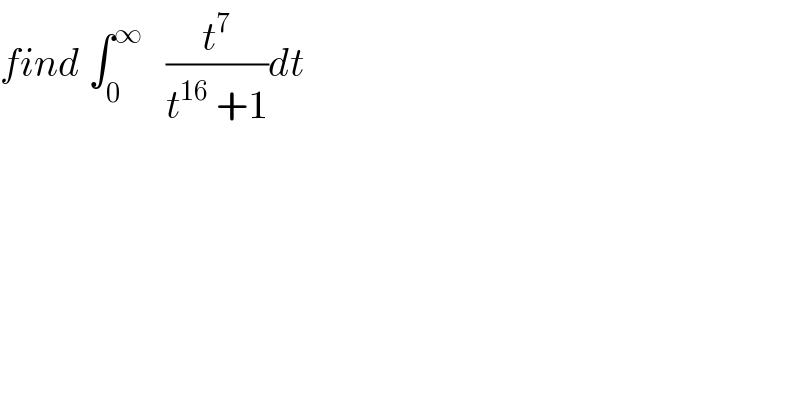
Commented by mathmax by abdo last updated on 13/Aug/19
![let f(y) =∫_0 ^y (t^7 /(t^(16) +1))dt ⇒f(y) =(1/8)∫_0 ^y ((8t^7 )/((t^8 )^2 +1))dt =(1/8)[arctan(t^8 )]_0 ^y =(1/8) arctan(y^8 ) ⇒∫_0 ^∞ (t^7 /(t^(16) +1))dt =lim_(y→+∞) f(y) =(1/8)(π/2) =(π/(16)) another way changement t=u^(1/(16)) give ∫_0 ^∞ (t^7 /(1+t^(16) ))dt =(1/(16)) ∫_0 ^∞ (u^(7/(16)) /(1+u)) u^((1/(16))−1) du =(1/(16))∫_0 ^∞ (u^((1/2)−1) /(1+u))du =(1/(16)) (π/(sin((π/2)))) =(π/(16)) by using the result ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) ( 0<a<1)](Q66375.png)
Commented by Prithwish sen last updated on 13/Aug/19

| ||
Question and Answers Forum | ||
Question Number 66346 by mathmax by abdo last updated on 12/Aug/19 | ||
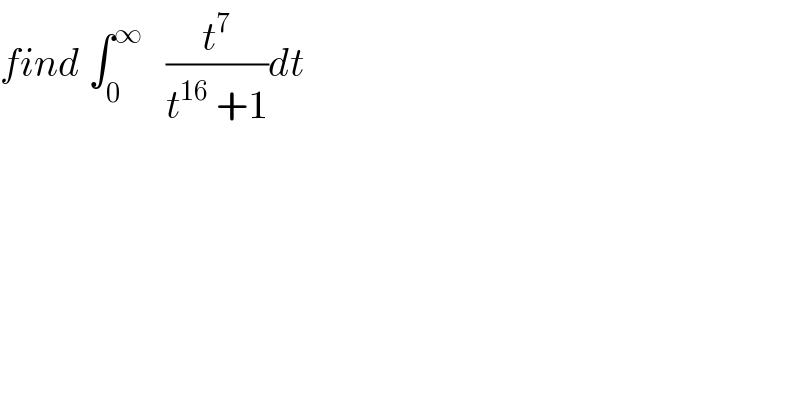 | ||
Commented by mathmax by abdo last updated on 13/Aug/19 | ||
![let f(y) =∫_0 ^y (t^7 /(t^(16) +1))dt ⇒f(y) =(1/8)∫_0 ^y ((8t^7 )/((t^8 )^2 +1))dt =(1/8)[arctan(t^8 )]_0 ^y =(1/8) arctan(y^8 ) ⇒∫_0 ^∞ (t^7 /(t^(16) +1))dt =lim_(y→+∞) f(y) =(1/8)(π/2) =(π/(16)) another way changement t=u^(1/(16)) give ∫_0 ^∞ (t^7 /(1+t^(16) ))dt =(1/(16)) ∫_0 ^∞ (u^(7/(16)) /(1+u)) u^((1/(16))−1) du =(1/(16))∫_0 ^∞ (u^((1/2)−1) /(1+u))du =(1/(16)) (π/(sin((π/2)))) =(π/(16)) by using the result ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) ( 0<a<1)](Q66375.png) | ||
Commented by Prithwish sen last updated on 13/Aug/19 | ||
 | ||