Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 66349 by mathmax by abdo last updated on 12/Aug/19

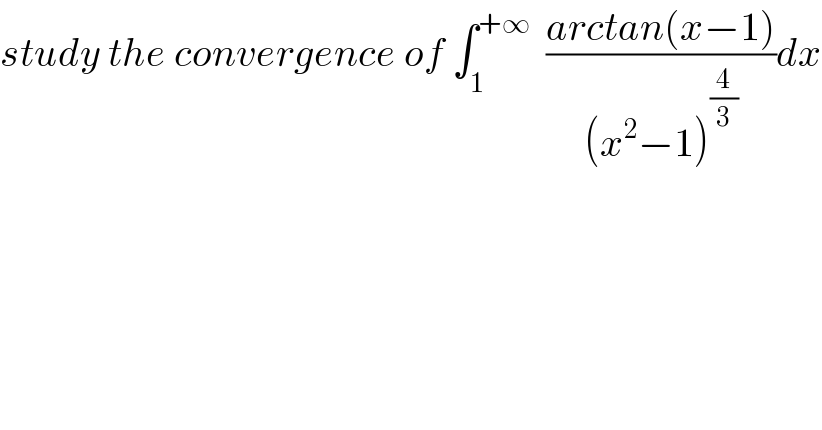
study the convergence of ∫_1 ^(+∞) ((arctan(x−1))/((x^2 −1)^(4/3) ))dx

$${study}\:{the}\:{convergence}\:{of}\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{arctan}\left({x}−\mathrm{1}\right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }{dx} \\ $$

Commented by mathmax by abdo last updated on 14/Aug/19

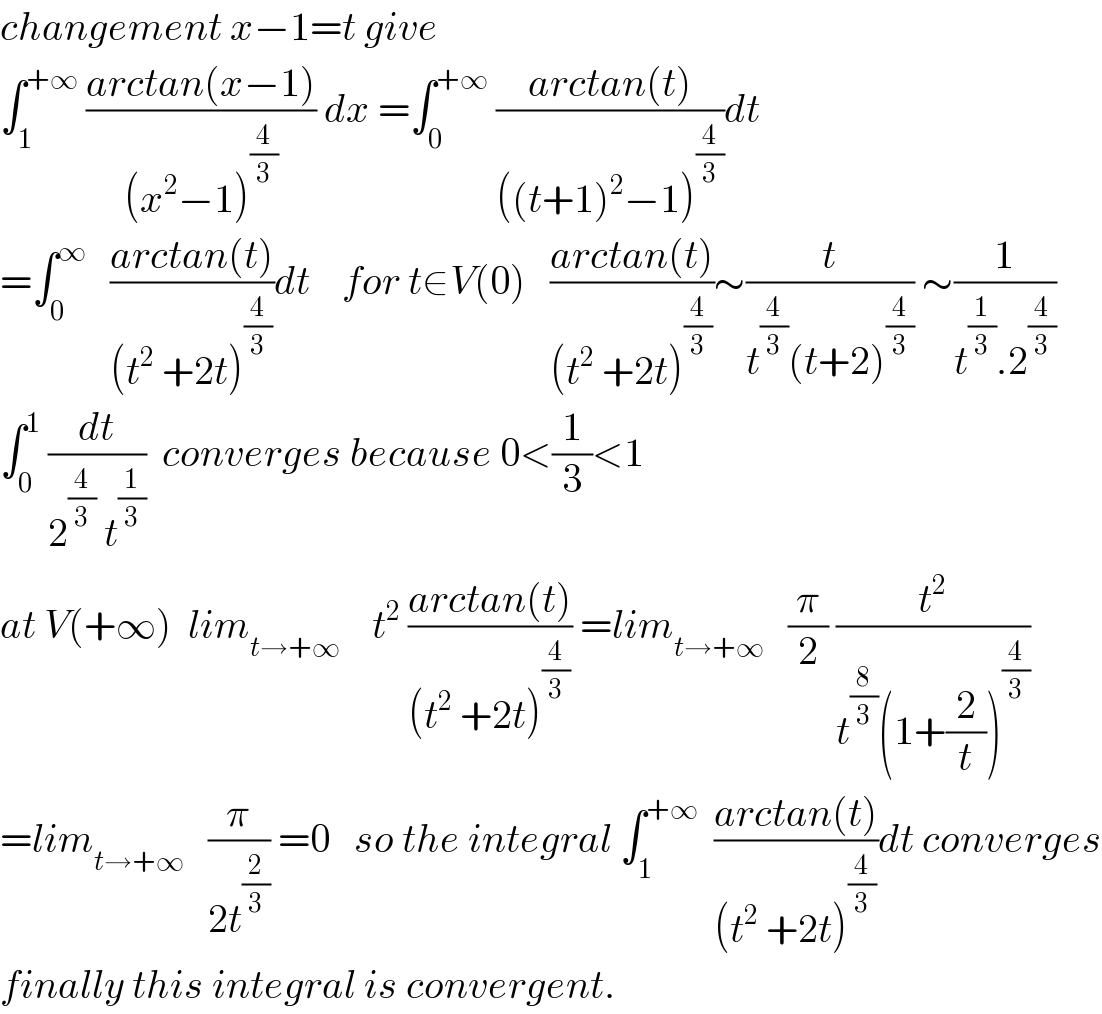
changement x−1=t give ∫_1 ^(+∞) ((arctan(x−1))/((x^2 −1)^(4/3) )) dx =∫_0 ^(+∞) ((arctan(t))/(((t+1)^2 −1)^(4/3) ))dt =∫_0 ^∞ ((arctan(t))/((t^2 +2t)^(4/3) ))dt for t∈V(0) ((arctan(t))/((t^2 +2t)^(4/3) ))∼(t/(t^(4/3) (t+2)^(4/3) )) ∼(1/(t^(1/3) .2^(4/3) )) ∫_0 ^1 (dt/(2^(4/3) t^(1/3) )) converges because 0<(1/3)<1 at V(+∞) lim_(t→+∞) t^2 ((arctan(t))/((t^2 +2t)^(4/3) )) =lim_(t→+∞) (π/2) (t^2 /(t^(8/3) (1+(2/t))^(4/3) )) =lim_(t→+∞) (π/(2t^(2/3) )) =0 so the integral ∫_1 ^(+∞) ((arctan(t))/((t^2 +2t)^(4/3) ))dt converges finally this integral is convergent.

$${changement}\:{x}−\mathrm{1}={t}\:{give} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{arctan}\left({x}−\mathrm{1}\right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }\:{dx}\:=\int_{\mathrm{0}} ^{+\infty} \:\frac{{arctan}\left({t}\right)}{\left(\left({t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left({t}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }{dt}\:\:\:\:{for}\:{t}\in{V}\left(\mathrm{0}\right)\:\:\:\frac{{arctan}\left({t}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }\sim\frac{{t}}{{t}^{\frac{\mathrm{4}}{\mathrm{3}}} \left({t}+\mathrm{2}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }\:\sim\frac{\mathrm{1}}{{t}^{\frac{\mathrm{1}}{\mathrm{3}}} .\mathrm{2}^{\frac{\mathrm{4}}{\mathrm{3}}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{2}^{\frac{\mathrm{4}}{\mathrm{3}}} \:{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:{converges}\:{because}\:\mathrm{0}<\frac{\mathrm{1}}{\mathrm{3}}<\mathrm{1} \\ $$$${at}\:{V}\left(+\infty\right)\:\:{lim}_{{t}\rightarrow+\infty} \:\:\:\:{t}^{\mathrm{2}} \:\frac{{arctan}\left({t}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }\:={lim}_{{t}\rightarrow+\infty} \:\:\:\frac{\pi}{\mathrm{2}}\:\frac{{t}^{\mathrm{2}} }{{t}^{\frac{\mathrm{8}}{\mathrm{3}}} \left(\mathrm{1}+\frac{\mathrm{2}}{{t}}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} } \\ $$$$={lim}_{{t}\rightarrow+\infty} \:\:\:\frac{\pi}{\mathrm{2}{t}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\mathrm{0}\:\:\:{so}\:{the}\:{integral}\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{arctan}\left({t}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} }{dt}\:{converges} \\ $$$${finally}\:{this}\:{integral}\:{is}\:{convergent}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com