Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 6635 by Rasheed Soomro last updated on 07/Jul/16

Commented by Rasheed Soomro last updated on 09/Jul/16

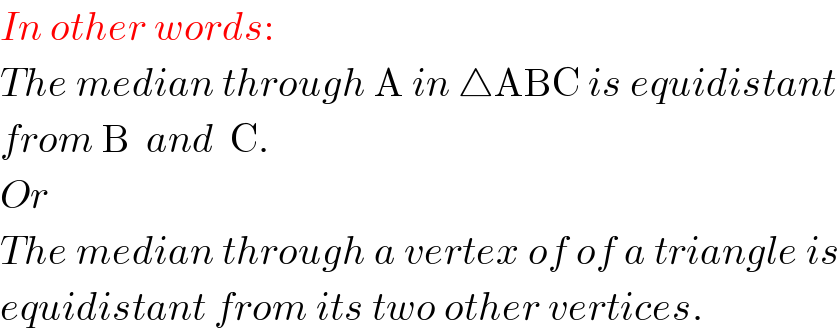
In other words: The median through A in △ABC is equidistant from B and C. Or The median through a vertex of of a triangle is equidistant from its two other vertices.

$${In}\:{other}\:{words}: \\ $$$${The}\:{median}\:{through}\:\mathrm{A}\:{in}\:\bigtriangleup\mathrm{ABC}\:{is}\:{equidistant} \\ $$$${from}\:\mathrm{B}\:\:{and}\:\:\mathrm{C}. \\ $$$${Or} \\ $$$${The}\:{median}\:{through}\:{a}\:{vertex}\:{of}\:{of}\:{a}\:{triangle}\:{is} \\ $$$${equidistant}\:{from}\:{its}\:{two}\:{other}\:{vertices}. \\ $$

Commented by Rasheed Soomro last updated on 07/Jul/16

In triangle ABC , D is the midpoint of BC AD^(↔) is a median-line. BE⊥AD^(↔) and CF⊥AD^(↔) Prove that ∣BE∣=∣CF∣.

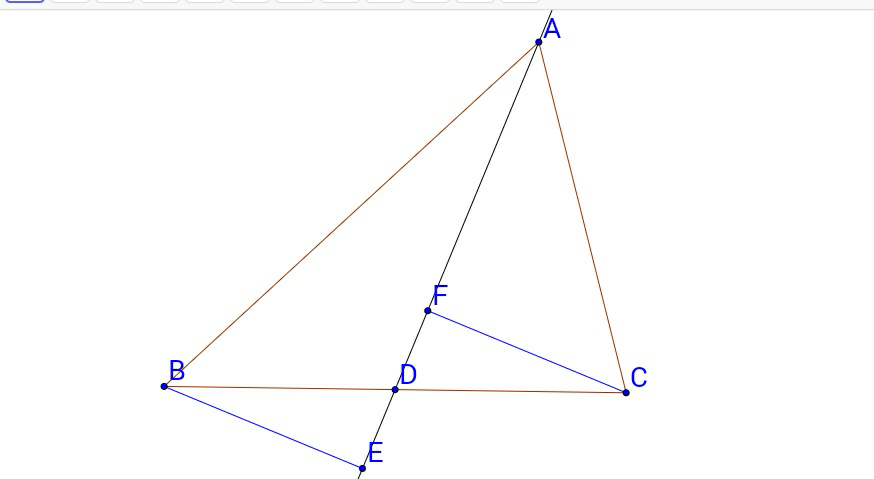
$${In}\:{triangle}\:\mathrm{ABC}\:,\:\mathrm{D}\:{is}\:{the}\:{midpoint}\:{of}\:\mathrm{BC} \\ $$$$\overset{\leftrightarrow} {\mathrm{AD}}\:\:{is}\:{a}\:\:{median}-{line}.\:\mathrm{BE}\bot\overset{\leftrightarrow} {\mathrm{AD}}\:{and}\:\:\mathrm{CF}\bot\overset{\leftrightarrow} {\mathrm{AD}} \\ $$$${Prove}\:{that}\:\mid\mathrm{BE}\mid=\mid\mathrm{CF}\mid. \\ $$

Answered by Yozzii last updated on 07/Jul/16

∠ADC=∠BDE since ∠ADC and ∠BDE are vertically opposite angles by virtue of the intersection of lines AE and BC. Also, ∣DC∣=∣BD∣>0 since line AD is a median of △ABC. Since ∠DFC=∠BED=90°, △DFC and △BED are right−angled triangles. Let θ=∠ADC=∠FDC (F lies between A and D on AD). Therefore, in △DFC, sinθ=((∣FC∣)/(∣DC∣)) and, in △BED, sinθ=((∣BE∣)/(∣BD∣)). Equating both expressions for sinθ we have ((∣FC∣)/(∣DC∣))=((∣BE∣)/(∣BD∣)). But, ∣DC∣=∣BD∣. ∴ ∣FC∣=∣BF∣ ■

$$\angle{ADC}=\angle{BDE}\:{since}\:\angle{ADC}\:{and} \\ $$$$\angle{BDE}\:{are}\:{vertically}\:{opposite}\:{angles} \\ $$$${by}\:{virtue}\:{of}\:{the}\:{intersection}\:{of}\:{lines} \\ $$$${AE}\:{and}\:{BC}.\:{Also},\:\mid{DC}\mid=\mid{BD}\mid>\mathrm{0} \\ $$$${since}\:{line}\:{AD}\:{is}\:{a}\:{median}\:{of}\:\bigtriangleup{ABC}. \\ $$$${Since}\:\angle{DFC}=\angle{BED}=\mathrm{90}°,\:\bigtriangleup{DFC}\: \\ $$$${and}\:\bigtriangleup{BED}\:{are}\:{right}−{angled}\:{triangles}. \\ $$$${Let}\:\theta=\angle{ADC}=\angle{FDC}\:\left({F}\:{lies}\:{between}\:{A}\:{and}\:{D}\:{on}\:{AD}\right).\:{Therefore},\:{in}\:\bigtriangleup{DFC}, \\ $$$${sin}\theta=\frac{\mid{FC}\mid}{\mid{DC}\mid}\:{and},\:{in}\:\bigtriangleup{BED},\:{sin}\theta=\frac{\mid{BE}\mid}{\mid{BD}\mid}. \\ $$$${Equating}\:{both}\:{expressions}\:{for}\:{sin}\theta\: \\ $$$${we}\:{have}\:\frac{\mid{FC}\mid}{\mid{DC}\mid}=\frac{\mid{BE}\mid}{\mid{BD}\mid}.\:{But},\:\mid{DC}\mid=\mid{BD}\mid. \\ $$$$\therefore\:\mid{FC}\mid=\mid{BF}\mid\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$

Commented by Rasheed Soomro last updated on 07/Jul/16

The triangles can also be proved congruent using A.S.A≊ A.S.A theorm.

$${The}\:{triangles}\:{can}\:\:{also}\:\mathrm{be}\:\:{proved}\:\mathrm{congruent}\:\:{using} \\ $$$$\mathrm{A}.\mathrm{S}.\mathrm{A}\approxeq\:\mathrm{A}.\mathrm{S}.\mathrm{A}\:\mathrm{theorm}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com