
Question and Answers Forum
Question Number 66351 by mathmax by abdo last updated on 12/Aug/19
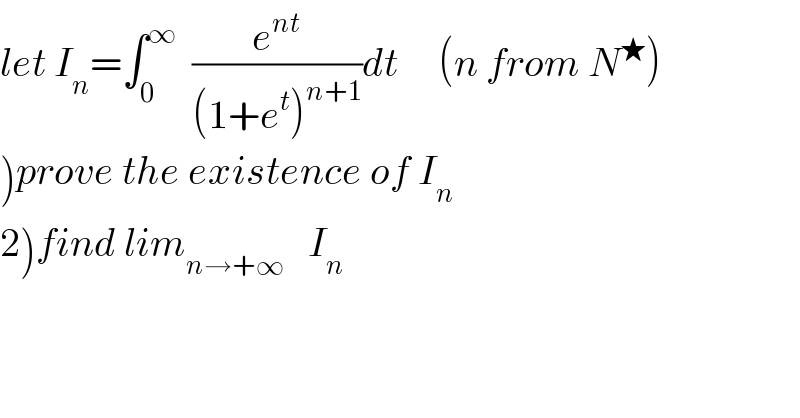
Commented by mathmax by abdo last updated on 15/Aug/19
![∀A>0 thefunction t→(e^(nt) /((1+e^t )^(n+1) )) is continue on [0,A] so integrable let see what happenat +∞ we have lim_(t→+∞) t^2 (e^(nt) /((1+e^t )^(n+1) )) =lim_(t→+∞) t^2 (e^(nt) /e^((n+1)t) ) =lim_(n→+∞) t^2 e^(−t) =0 so I_n is convergent 2)changement e^(nt) =x give nt=ln(x) ⇒ I_n =∫_1 ^(+∞) (x/((1+x^(1/n) )^(n+1) )) (dx/(nx)) =∫_1 ^(+∞) (dx/((1+x^(1/n) )^(n+1) )) =∫_1 ^(+∞) e^(−(n+1)ln(1+x^(1/n) )) dx =∫_R f_n (x)dx with f_n (x)=e^(−(n+1)ln(1+x^(1/n) )) χ_([1,+∞[) (x) we have f_n )continues and f_n →^(cs) 0 ⇒lim_(n→+∞) I_n =∫_R lim_(n→+∞) f_n (x)dx =0](Q66454.png)
| ||
Question and Answers Forum | ||
Question Number 66351 by mathmax by abdo last updated on 12/Aug/19 | ||
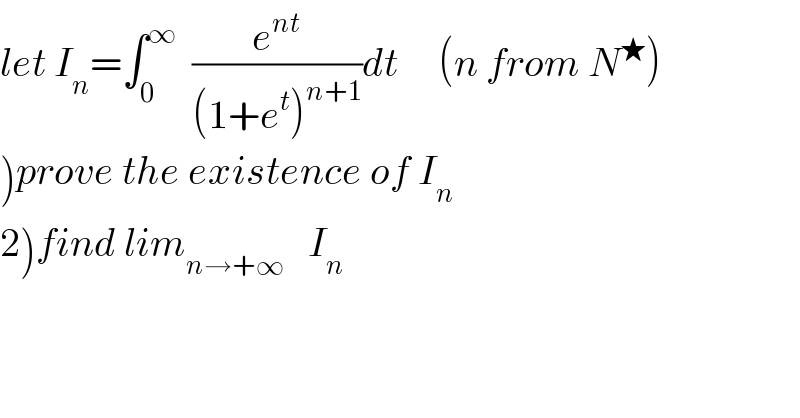 | ||
Commented by mathmax by abdo last updated on 15/Aug/19 | ||
![∀A>0 thefunction t→(e^(nt) /((1+e^t )^(n+1) )) is continue on [0,A] so integrable let see what happenat +∞ we have lim_(t→+∞) t^2 (e^(nt) /((1+e^t )^(n+1) )) =lim_(t→+∞) t^2 (e^(nt) /e^((n+1)t) ) =lim_(n→+∞) t^2 e^(−t) =0 so I_n is convergent 2)changement e^(nt) =x give nt=ln(x) ⇒ I_n =∫_1 ^(+∞) (x/((1+x^(1/n) )^(n+1) )) (dx/(nx)) =∫_1 ^(+∞) (dx/((1+x^(1/n) )^(n+1) )) =∫_1 ^(+∞) e^(−(n+1)ln(1+x^(1/n) )) dx =∫_R f_n (x)dx with f_n (x)=e^(−(n+1)ln(1+x^(1/n) )) χ_([1,+∞[) (x) we have f_n )continues and f_n →^(cs) 0 ⇒lim_(n→+∞) I_n =∫_R lim_(n→+∞) f_n (x)dx =0](Q66454.png) | ||