Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 66468 by mathmax by abdo last updated on 15/Aug/19

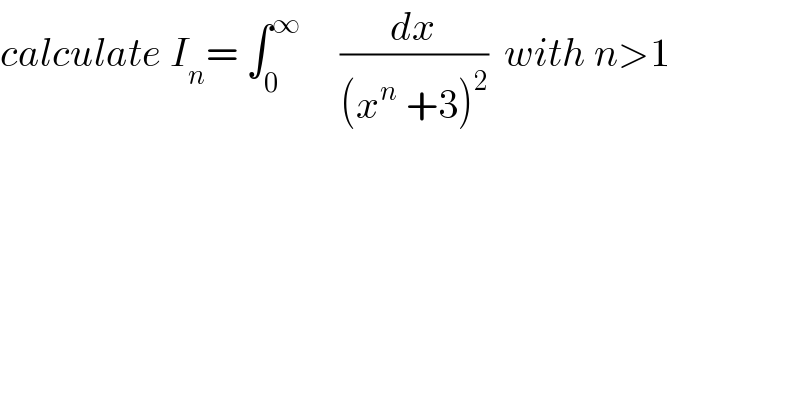
calculate I_n = ∫_0 ^∞ (dx/((x^n +3)^2 )) with n>1

$${calculate}\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{{n}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:\:{with}\:{n}>\mathrm{1} \\ $$

Commented bymathmax by abdo last updated on 16/Aug/19

let f(a) =∫_0 ^∞ (dx/(a +x^n )) with a>0 ⇒f(a) =(1/a)∫_0 ^∞ (dx/((1+(x^n /a)))) let use the changement (x^n /a) =u^n ⇒x^n =a u^n ⇒x=a^(1/n) u ⇒ f(a) =(1/a)∫_0 ^∞ (1/(1+u^n ))a^(1/n) du =a^((1/n)−1) ∫_0 ^∞ (du/(1+u^n )) changement u=α^(1/n) give ∫_0 ^∞ (1/(1+α))(1/n)α^((1/n)−1) dα =(1/n) ∫_0 ^∞ (α^((1/n)−1) /(1+α))dα =(1/n) (π/(sin((π/n)))) ⇒ f(a) =a^((1/n)−1) ×(π/(nsin((π/n)))) =((π a^((1/n)−1) )/(nsin((π/n)))) and we have f^′ (a) =−∫_0 ^∞ (dx/((a+x^n )^2 )) ⇒∫_0 ^∞ (dx/((a+x^n )^2 )) =−f^′ (a) f^′ (a) =((π((1/n)−1)a^((1/n)−2) )/(nsin((π/n)))) ⇒∫_0 ^∞ (dx/((a+x^n )^2 )) =((π(1−(1/n))a^((1/n)−2) )/(nsin((π/n)))) a=3 ⇒ ∫_0 ^∞ (dx/((3+x^n )^2 )) =((π(1−(1/n))3^((1/n)−2) )/(nsin((π/n)))) =I_n

$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{a}\:+{x}^{{n}} }\:\:\:{with}\:{a}>\mathrm{0}\:\Rightarrow{f}\left({a}\right)\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left(\mathrm{1}+\frac{{x}^{{n}} }{{a}}\right)} \\ $$ $${let}\:{use}\:{the}\:{changement}\:\:\frac{{x}^{{n}} }{{a}}\:={u}^{{n}} \:\Rightarrow{x}^{{n}} \:={a}\:{u}^{{n}} \:\Rightarrow{x}={a}^{\frac{\mathrm{1}}{{n}}} \:{u}\:\Rightarrow \\ $$ $${f}\left({a}\right)\:=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{{n}} }{a}^{\frac{\mathrm{1}}{{n}}} \:{du}\:={a}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mathrm{1}+{u}^{{n}} }\:{changement}\:{u}=\alpha^{\frac{\mathrm{1}}{{n}}} \\ $$ $${give}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+\alpha}\frac{\mathrm{1}}{{n}}\alpha^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:{d}\alpha\:=\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\alpha^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\mathrm{1}+\alpha}{d}\alpha\:=\frac{\mathrm{1}}{{n}}\:\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)}\:\Rightarrow \\ $$ $${f}\left({a}\right)\:={a}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} ×\frac{\pi}{{nsin}\left(\frac{\pi}{{n}}\right)}\:=\frac{\pi\:{a}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{{nsin}\left(\frac{\pi}{{n}}\right)}\:\:{and}\:{we}\:{have} \\ $$ $${f}^{'} \left({a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({a}+{x}^{{n}} \right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left({a}+{x}^{{n}} \right)^{\mathrm{2}} }\:=−{f}^{'} \left({a}\right) \\ $$ $${f}^{'} \left({a}\right)\:=\frac{\pi\left(\frac{\mathrm{1}}{{n}}−\mathrm{1}\right){a}^{\frac{\mathrm{1}}{{n}}−\mathrm{2}} }{{nsin}\left(\frac{\pi}{{n}}\right)}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({a}+{x}^{{n}} \right)^{\mathrm{2}} }\:=\frac{\pi\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right){a}^{\frac{\mathrm{1}}{{n}}−\mathrm{2}} }{{nsin}\left(\frac{\pi}{{n}}\right)} \\ $$ $${a}=\mathrm{3}\:\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left(\mathrm{3}+{x}^{{n}} \right)^{\mathrm{2}} }\:=\frac{\pi\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)\mathrm{3}^{\frac{\mathrm{1}}{{n}}−\mathrm{2}} }{{nsin}\left(\frac{\pi}{{n}}\right)}\:={I}_{{n}} \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com