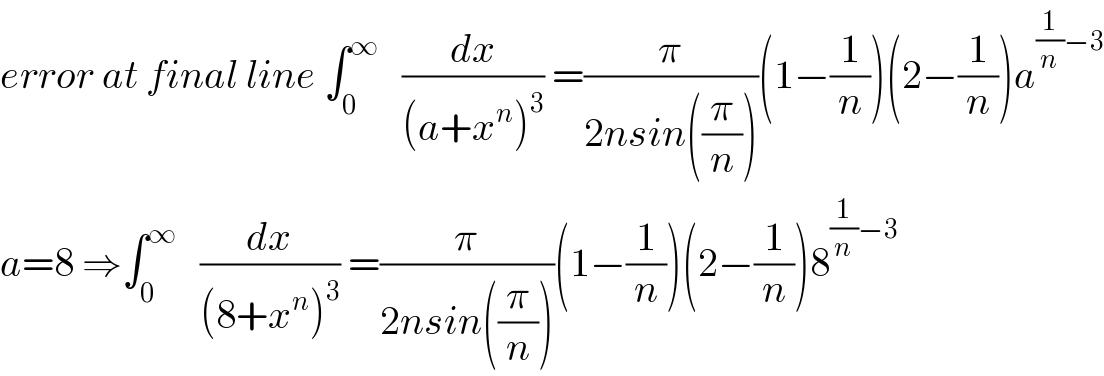Question and Answers Forum
Question Number 66470 by mathmax by abdo last updated on 15/Aug/19
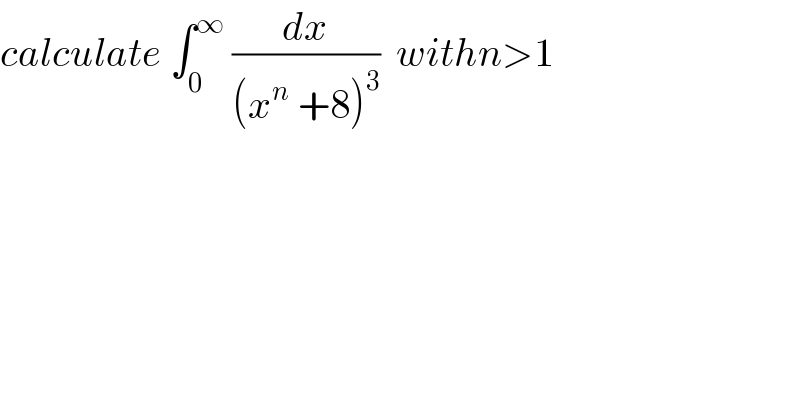
Commented by~ À ® @ 237 ~ last updated on 16/Aug/19
![let state ∀ a>0 f(a)=∫_0 ^∞ (dx/((x^n +a)^2 )) f(a)=∫_0 ^∞ (dx/(a^2 [((x/a^(1/n) ))^n +1]^2 )) when changing x=a^(1/n) u we get f(a)= a^((1/n) −2) ∫_0 ^∞ (du/((u^n +1)^2 )) now change v=(1/(u^n +1)) ⇒ u=((1/v) −1)^(1/n) ⇒ du=(1/n).(((−1)/v^2 ))((1/v) −1)^((1/n) −1) dv then f(a)=(1/n). a^((1/n)−2) ∫_0 ^1 v^2 .((1/v^2 ))((1/v) −1)^((1/n) −1) dv = (a^((1/n)−2) /n) ∫_0 ^1 v^(1−(1/n)) (1−v)^((1/n)−1) dv = (a^((1/n) −2) /n) B(2−(1/n) , (1/n)) = (a^((1/n) −2) /n) .((Γ(2−(1/n))Γ((1/n)))/(Γ(2))) as Γ(x+1)=xΓ(x) we have Γ(2−(1/n))=(1−(1/n))Γ(1−(1/n)) and Γ(2)=Γ(1)=1 So f(a)=(a^((1/n) −2) /n) .(1−(1/n))Γ(1−(1/n))Γ((1/n)) as Γ(1−z)Γ(z)=(π/(sin(πz))) we finally get f(a)= (1/n)(1−(1/n))a^((1/n) −2) .(π/(sin((π/n)))) Now we can deduce f(8) , f(3), f(n)](Q66488.png)
Commented by~ À ® @ 237 ~ last updated on 16/Aug/19
![if ∀ p>2 g_p (a)=∫_0 ^∞ (dx/((x^n +a)^p )) start as the previous and reach to g_p (a)=(a^((1/n) −p) /n) ∫_(0 ) ^1 v^p .((1/v^2 ))((1/v)−1)^((1/n)−1) dv = (a^((1/n) −p) /n) ∫_0 ^1 v^(p−2+1−(1/n)) (1−v)^((1/n)−1) dv =(a^((1/n)−p) /n) B(p−(1/n), (1/n)) =(a^((1/n)−p) /n) .((Γ(p−(1/n))Γ((1/n)))/(Γ(p))) as Γ(p+z)=z(z+1).......(z+p−1)Γ(z) we have Γ(p−(1/n))=Γ(p−1+(1−(1/n)))=Π_(k=0) ^(p−2) [(1−(1/n))+k] Γ(1−(1/n)) Now g_p (a)=(a^((1/n) −p) /(n.(p−1)!)) .(Π_(k=0) ^(p−2) [(1−(1/n))+k]) Γ(1−(1/n))Γ((1/n)) =(a^((1/n)−p) /(n.(p−1)!)) .(π/(sin((π/n)))) .Π_(k=0) ^(p−2) [(1−(1/n))+k] now we can deduce g_3 (8) ,∙.......](Q66490.png)
Commented bymathmax by abdo last updated on 16/Aug/19

Commented bymathmax by abdo last updated on 16/Aug/19
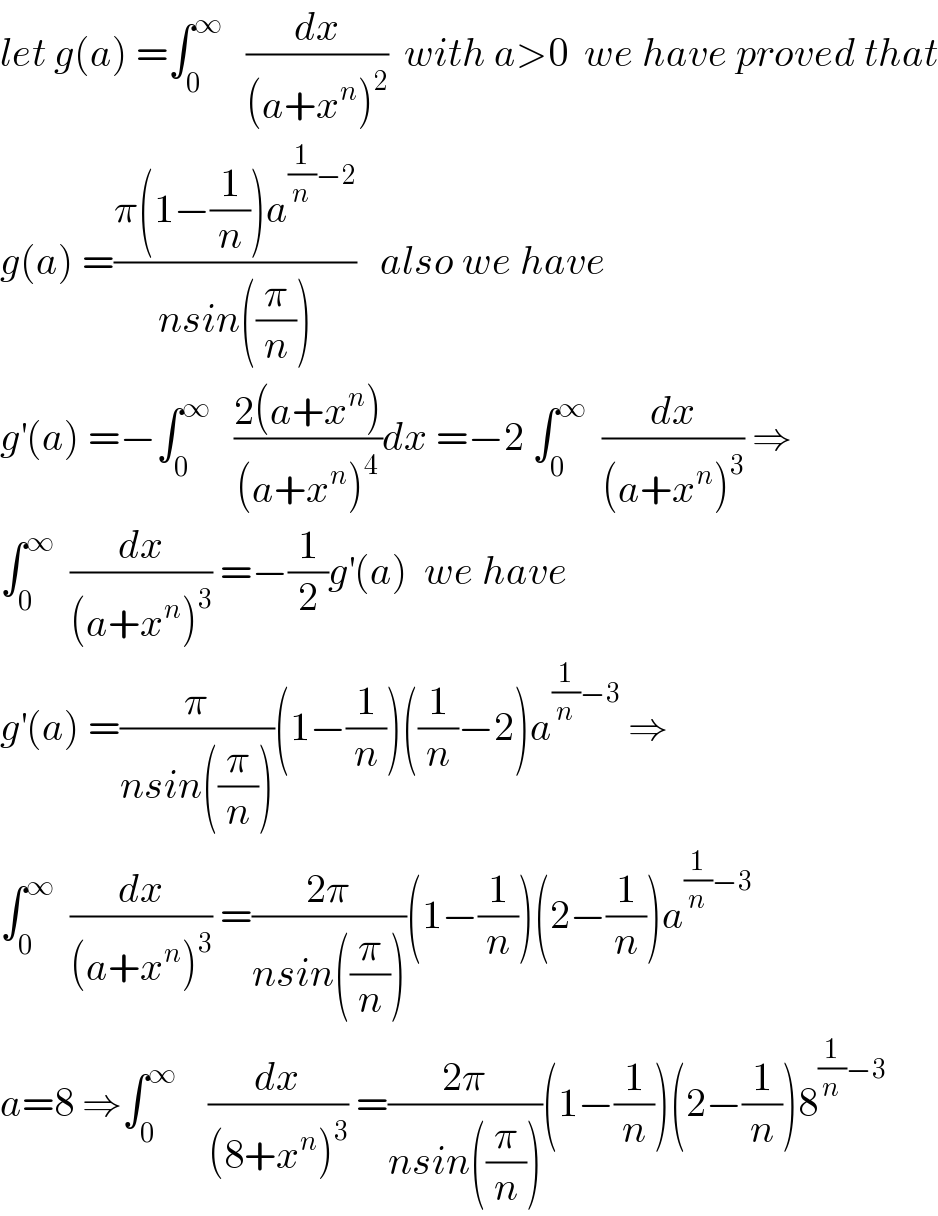
Commented bymathmax by abdo last updated on 16/Aug/19