Question Number 66513 by Rio Michael last updated on 16/Aug/19
$${when}\:{finding}\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2}{x}\:+\mathrm{4}\right)^{\mathrm{5}} {dx}\: \\ $$$${must}\:{we}\:{change}\:{limits}? \\ $$
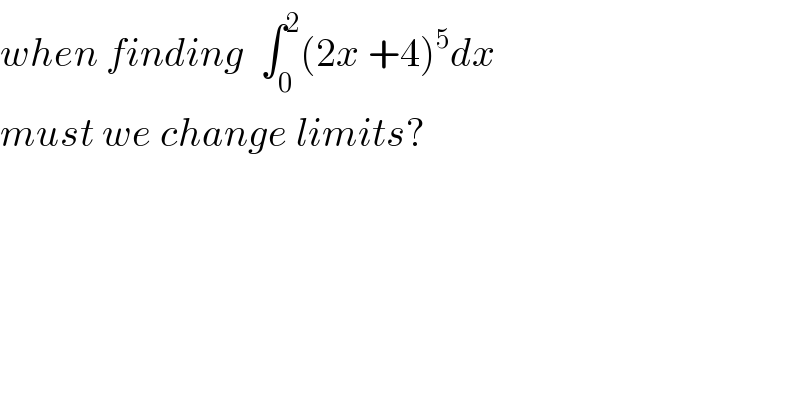
Commented by kaivan.ahmadi last updated on 17/Aug/19
$${yes}.{since}\:{we}\:{must}\:{change}\:{the}\:{parameter} \\ $$$${t}=\mathrm{2}{x}+\mathrm{4}\Rightarrow{dt}=\mathrm{2}{dx}\:\: \\ $$$$\begin{cases}{{x}=\mathrm{0}\Rightarrow{t}=\mathrm{4}}\\{{x}=\mathrm{2}\Rightarrow{t}=\mathrm{8}}\end{cases} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{4}} ^{\mathrm{8}} {t}^{\mathrm{5}} {dt}=\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{8}^{\mathrm{6}} −\mathrm{4}^{\mathrm{6}} \right)=\frac{\mathrm{1}}{\mathrm{12}}×\mathrm{4}^{\mathrm{6}} \left(\mathrm{2}^{\mathrm{6}} −\mathrm{1}\right)=\frac{\mathrm{63}}{\mathrm{2}}×\mathrm{4}^{\mathrm{6}} \\ $$
Commented by Rio Michael last updated on 17/Aug/19
$${thank}\:{you}\:{sir}. \\ $$
Commented by Cmr 237 last updated on 17/Aug/19
![no⊛ 0.5∫_4 ^8 t^5 dt=0.5×−_6 ^1 [t^6 ]_4 ^8 =−_(12) ^1 [8^6 −4^6 ] =21504 (( [(),() ]),() )](Q66571.png)
$${no}\circledast \\ $$$$\mathrm{0}.\mathrm{5}\int_{\mathrm{4}} ^{\mathrm{8}} {t}^{\mathrm{5}} {dt}=\mathrm{0}.\mathrm{5}×\underset{\mathrm{6}} {\overset{\mathrm{1}} {−}}\left[{t}^{\mathrm{6}} \right]_{\mathrm{4}} ^{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{12}} {\overset{\mathrm{1}} {−}}\left[\mathrm{8}^{\mathrm{6}} −\mathrm{4}^{\mathrm{6}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{21504}\begin{pmatrix}{\begin{bmatrix}{}\\{}\end{bmatrix}}\\{}\end{pmatrix} \\ $$
Commented by kaivan.ahmadi last updated on 17/Aug/19
$${thank}\:{you}\:{sir} \\ $$
Answered by mr W last updated on 18/Aug/19
![you mustn′t change limits, if you proceed like this: ∫_0 ^2 (2x +4)^5 dx =(1/2)∫_0 ^2 (2x +4)^5 d(2x+4) =(1/(2×6))[(2x+4)^6 ]_0 ^2 =(1/(12))[8^6 −4^6 ] =21504](Q66669.png)
$${you}\:{mustn}'{t}\:{change}\:{limits},\:{if}\:{you} \\ $$$${proceed}\:{like}\:{this}: \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2}{x}\:+\mathrm{4}\right)^{\mathrm{5}} {dx}\: \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{2}{x}\:+\mathrm{4}\right)^{\mathrm{5}} {d}\left(\mathrm{2}{x}+\mathrm{4}\right) \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}×\mathrm{6}}\left[\left(\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{6}} \right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left[\mathrm{8}^{\mathrm{6}} −\mathrm{4}^{\mathrm{6}} \right] \\ $$$$=\mathrm{21504} \\ $$
Commented by Rio Michael last updated on 19/Aug/19
$${thanks}\:{sir} \\ $$