
Question and Answers Forum
Question Number 67471 by AnjanDey last updated on 27/Aug/19
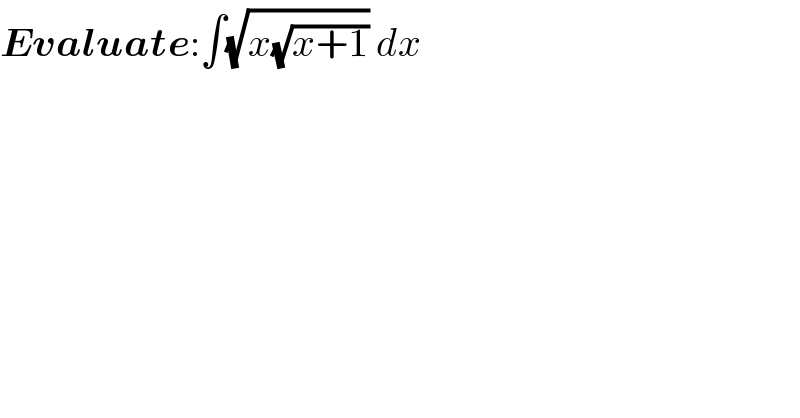
Commented by MJS last updated on 28/Aug/19
![∫(√(x(√(x+1))))dx= [t=(√x) → dx=2(√x)dt] =2∫t^2 (t^2 +1)^(1/4) dt= =−(4/(21))∫(dt/((t^2 +1)^(3/4) ))+2∫((t^4 +t^2 +(2/(21)))/((t^2 +1)^(3/4) ))dt =−(4/(21))∫(dt/((t^2 +1)^(3/4) ))+(4/(21))t(3t^2 +1)(t^2 +1)^(1/4) ...I cannot solve the 1^(st) one plus I somehow solved the 2^(nd) one but I really don′t remember how... I lost some papers... anyway (d/dt)[(4/(21))t(3t^2 +1)(t^2 +1)^(1/4) ]=2((t^4 +t^2 +(2/(21)))/((t^2 +1)^(3/4) )) and −(4/(21(t^2 +1)^(3/4) ))+2((t^4 +t^2 +(2/(21)))/((t^2 +1)^(3/4) ))=2t^2 (t^2 +1)^(1/4)](Q67490.png)
Commented by Abdo msup. last updated on 28/Aug/19

Commented by Abdo msup. last updated on 28/Aug/19
Commented by MJS last updated on 28/Aug/19

