Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 66589 by Tanmay chaudhury last updated on 17/Aug/19

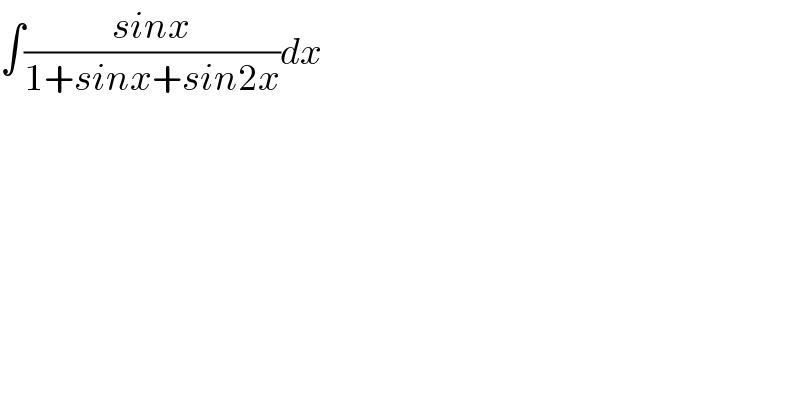
∫((sinx)/(1+sinx+sin2x))dx

$$\int\frac{{sinx}}{\mathrm{1}+{sinx}+{sin}\mathrm{2}{x}}{dx} \\ $$

Commented by MJS last updated on 17/Aug/19

Weierstrass [t=tan (x/2) → dx=((2dt)/(t^2 +1))] leads to 4∫(t/((t+1)(t^3 −3t^2 +5t+1)))dt t^3 −3t^2 +5t+1= =(t−α−β−1)(t^2 +(α+β−2)t+(α^2 +β^2 −αβ−α−β+1)) α=((−2−(2/9)(√(87))))^(1/3) β=((−2+(2/9)(√(87))))^(1/3) α+β+1=A α+β−2=B α^2 +β^2 −αβ−α−β+1=C 4∫(t/((t+1)(t−A)(t^2 +Bt+C)))dt= =−(4/((A+1)(B−C−1)))∫(dt/(t+1))+ +((4A)/((A+1)(A^2 +AB+C)))∫(dt/(t−A))+ +(4/((A^2 +AB+C)(B−C−1)))∫(((A+C)t+(A+B−1)C)/(t^2 +Bt+C))dt now solve these... I found no easier path

$$\mathrm{Weierstrass}\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right]\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{4}\int\frac{{t}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{5}{t}+\mathrm{1}\right)}{dt} \\ $$$${t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{5}{t}+\mathrm{1}= \\ $$$$=\left({t}−\alpha−\beta−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\left(\alpha+\beta−\mathrm{2}\right){t}+\left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} −\alpha\beta−\alpha−\beta+\mathrm{1}\right)\right) \\ $$$$\alpha=\sqrt[{\mathrm{3}}]{−\mathrm{2}−\frac{\mathrm{2}}{\mathrm{9}}\sqrt{\mathrm{87}}}\:\:\beta=\sqrt[{\mathrm{3}}]{−\mathrm{2}+\frac{\mathrm{2}}{\mathrm{9}}\sqrt{\mathrm{87}}} \\ $$$$\alpha+\beta+\mathrm{1}={A} \\ $$$$\alpha+\beta−\mathrm{2}={B} \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} −\alpha\beta−\alpha−\beta+\mathrm{1}={C} \\ $$$$\mathrm{4}\int\frac{{t}}{\left({t}+\mathrm{1}\right)\left({t}−{A}\right)\left({t}^{\mathrm{2}} +{Bt}+{C}\right)}{dt}= \\ $$$$=−\frac{\mathrm{4}}{\left({A}+\mathrm{1}\right)\left({B}−{C}−\mathrm{1}\right)}\int\frac{{dt}}{{t}+\mathrm{1}}+ \\ $$$$\:\:\:\:\:+\frac{\mathrm{4}{A}}{\left({A}+\mathrm{1}\right)\left({A}^{\mathrm{2}} +{AB}+{C}\right)}\int\frac{{dt}}{{t}−{A}}+ \\ $$$$\:\:\:\:\:+\frac{\mathrm{4}}{\left({A}^{\mathrm{2}} +{AB}+{C}\right)\left({B}−{C}−\mathrm{1}\right)}\int\frac{\left({A}+{C}\right){t}+\left({A}+{B}−\mathrm{1}\right){C}}{{t}^{\mathrm{2}} +{Bt}+{C}}{dt} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{these}... \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{easier}\:\mathrm{path} \\ $$

Commented by MJS last updated on 17/Aug/19

...corrected a mistake

$$...\mathrm{corrected}\:\mathrm{a}\:\mathrm{mistake} \\ $$

Commented by Tanmay chaudhury last updated on 17/Aug/19

excellent sir...i shall try to complete

$${excellent}\:{sir}...{i}\:{shall}\:{try}\:{to}\:{complete}\: \\ $$

Commented by mathmax by abdo last updated on 18/Aug/19

let I =∫ ((sinx)/(1+sinx +sin(2x)))dx ⇒ I =∫ ((sinx)/(1+sinx +2sinx cosx))dx changement tan((x/2))=t give I =∫ (((2t)/(1+t^2 ))/(1+((2t)/(1+t^2 ))+2 ((2t)/(1+t^2 ))((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫((4t)/((1+t^2 )^2 {1+((2t)/(1+t^2 )) +((4t(1−t^2 ))/((1+t^2 )^2 ))}))dt =∫ ((4tdt)/((1+t^2 )^2 +2t(1+t^2 )+4t(1−t^2 ))) =∫ ((4tdt)/(t^4 +2t^2 +1+2t+2t^3 +4t−4t^3 )) =∫ ((4tdt)/(t^4 −2t^3 +2t^2 +6t +1)) let decompose the fraction F(t) =((4t)/(t^4 −2t^3 +2t^2 +6t +1)) t^4 −2t^3 +2t^2 +6t +1 =0 the roots are t_1 =1,5898 +1,7445i (complex) t_2 ∼1,5898−1,7445i (complex) t_3 =−1 (real) t_4 ∼−0,1795 (real) ⇒ F(t)∼ ((4t)/((t−t_1 )(t−t_1 ^− )(t+1)(t−t_4 ))) =((4t)/((t^2 −2Re(t_1 )t +∣t_1 ∣^2 )(t+1)(t−t_4 ))) =(a/(t+1)) +(b/(t−t_4 )) +((ct+d)/(t^2 −2Re(t_1 )t +∣t_1 ∣^2 )) ⇒I =aln∣t+1∣+bln∣t−t_4 ∣ +∫ ((ct +d)/(t^2 −2Re(t_1 )t +∣t_1 ∣^2 )) rest to calculate a,b,c and d....becontinued....

$${let}\:{I}\:=\int\:\frac{{sinx}}{\mathrm{1}+{sinx}\:+{sin}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow\:{I}\:=\int\:\:\frac{{sinx}}{\mathrm{1}+{sinx}\:+\mathrm{2}{sinx}\:{cosx}}{dx} \\ $$$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\: \\ $$$${I}\:=\int\:\:\:\:\:\frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{2}\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\frac{\mathrm{4}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left\{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\frac{\mathrm{4}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}}{dt} \\ $$$$=\int\:\:\:\frac{\mathrm{4}{tdt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{2}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{4}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\:=\int\:\:\frac{\mathrm{4}{tdt}}{{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{2}{t}+\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{4}{t}−\mathrm{4}{t}^{\mathrm{3}} } \\ $$$$=\int\:\:\frac{\mathrm{4}{tdt}}{{t}^{\mathrm{4}} \:−\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{6}{t}\:+\mathrm{1}}\:{let}\:{decompose}\:{the}\:{fraction} \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{4}{t}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{6}{t}\:+\mathrm{1}} \\ $$$${t}^{\mathrm{4}} \:−\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{6}{t}\:+\mathrm{1}\:=\mathrm{0}\:\:{the}\:{roots}\:{are}\: \\ $$$${t}_{\mathrm{1}} =\mathrm{1},\mathrm{5898}\:+\mathrm{1},\mathrm{7445}{i}\:\left({complex}\right) \\ $$$${t}_{\mathrm{2}} \sim\mathrm{1},\mathrm{5898}−\mathrm{1},\mathrm{7445}{i}\:\left({complex}\right) \\ $$$${t}_{\mathrm{3}} =−\mathrm{1}\:\:\left({real}\right) \\ $$$${t}_{\mathrm{4}} \sim−\mathrm{0},\mathrm{1795}\:\left({real}\right)\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{F}\left({t}\right)\sim\:\frac{\mathrm{4}{t}}{\left({t}−{t}_{\mathrm{1}} \right)\left({t}−\overset{−} {{t}}_{\mathrm{1}} \right)\left({t}+\mathrm{1}\right)\left({t}−{t}_{\mathrm{4}} \right)} \\ $$$$=\frac{\mathrm{4}{t}}{\left({t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:\:+\mid{t}_{\mathrm{1}} \mid^{\mathrm{2}} \right)\left({t}+\mathrm{1}\right)\left({t}−{t}_{\mathrm{4}} \right)}\:=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{b}}{{t}−{t}_{\mathrm{4}} }\:+\frac{{ct}+{d}}{{t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:+\mid{t}_{\mathrm{1}} \mid^{\mathrm{2}} } \\ $$$$\Rightarrow{I}\:={aln}\mid{t}+\mathrm{1}\mid+{bln}\mid{t}−{t}_{\mathrm{4}} \mid\:\:+\int\:\:\:\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} −\mathrm{2}{Re}\left({t}_{\mathrm{1}} \right){t}\:+\mid{t}_{\mathrm{1}} \mid^{\mathrm{2}} } \\ $$$${rest}\:{to}\:{calculate}\:{a},{b},{c}\:{and}\:{d}....{becontinued}.... \\ $$

Commented by ~ À ® @ 237 ~ last updated on 18/Aug/19

Let named it F(x) We can explicit the denominator 1+sinx+sin(2x)= Im (1+e^(ix) +e^(i2x) )=Im(((e^(i3x) −1)/(e^(ix) −1)))=Im(((e^(i((3x)/2)) (e^(i((3x)/2)) −e^(−i((3x)/2)) ))/(e^(i(x/2)) (e^(i(x/2)) −e^(−i(x/2)) ))))=Im(((e^(ix) . sin(((3x)/2)))/(sin((x/2)))))=((sin(3((x/2))))/(sin((x/2)))) Im(e^(ix) )= (3−4sin^2 ((x/2))) sinx using (sin3θ= 3sinθ −4sin^3 θ ) Now F(x)= ∫ (( dx)/(3−4sin^2 ((x/2)))) = 2G(u) avec G(u)= ∫ (du/(3−4sin^2 u)) ( stating x=2u ) G(u)= ∫ ((1/(cos^2 u))/((3/(cos^2 u))−4tan^2 u)) du = ∫((1+tan^2 u)/(3 −tan^2 u)) du ( remember (1/(cos^2 u))=1+tan^2 u ) = (1/3) ∫ (((1+tan^2 u))/(1−(((tanu)/((√3) )))^2 )) du = (1/(√3)) argth(((tanu)/((√3) ))) + c Finally we get F(x)= (2/(√3)) argth(((tan((x/2)))/(√3))) + k

$${Let}\:{named}\:{it}\:{F}\left({x}\right)\: \\ $$$${We}\:\:{can}\:{explicit}\:{the}\:{denominator}\: \\ $$$$\mathrm{1}+{sinx}+{sin}\left(\mathrm{2}{x}\right)=\:{Im}\:\left(\mathrm{1}+{e}^{{ix}} +{e}^{{i}\mathrm{2}{x}} \right)={Im}\left(\frac{{e}^{{i}\mathrm{3}{x}} −\mathrm{1}}{{e}^{{ix}} −\mathrm{1}}\right)={Im}\left(\frac{{e}^{{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \left({e}^{{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} −{e}^{−{i}\frac{\mathrm{3}{x}}{\mathrm{2}}} \right)}{{e}^{{i}\frac{{x}}{\mathrm{2}}} \left({e}^{{i}\frac{{x}}{\mathrm{2}}} −{e}^{−{i}\frac{{x}}{\mathrm{2}}} \right)}\right)={Im}\left(\frac{{e}^{{ix}} .\:{sin}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\right)=\frac{{sin}\left(\mathrm{3}\left(\frac{{x}}{\mathrm{2}}\right)\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\:{Im}\left({e}^{{ix}} \right)=\:\left(\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:{sinx}\:\:\:\:\:\:\:\:{using}\:\left({sin}\mathrm{3}\theta=\:\mathrm{3}{sin}\theta\:−\mathrm{4}{sin}^{\mathrm{3}} \theta\:\right) \\ $$$${Now}\: \\ $$$${F}\left({x}\right)=\:\int\:\frac{\:{dx}}{\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\:=\:\mathrm{2}{G}\left({u}\right)\:\:\:\:\:\:\:\:{avec}\:\:{G}\left({u}\right)=\:\int\:\frac{{du}}{\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} {u}}\:\:\:\left(\:{stating}\:{x}=\mathrm{2}{u}\:\right) \\ $$$${G}\left({u}\right)=\:\int\:\frac{\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {u}}}{\frac{\mathrm{3}}{{cos}^{\mathrm{2}} {u}}−\mathrm{4}{tan}^{\mathrm{2}} {u}}\:{du}\:=\:\int\frac{\mathrm{1}+{tan}^{\mathrm{2}} {u}}{\mathrm{3}\:−{tan}^{\mathrm{2}} {u}}\:{du}\:\:\:\:\:\left(\:{remember}\:\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {u}}=\mathrm{1}+{tan}^{\mathrm{2}} {u}\:\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{3}}\:\int\:\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right)}{\mathrm{1}−\left(\frac{{tanu}}{\sqrt{\mathrm{3}}\:}\right)^{\mathrm{2}} }\:{du}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:\:{argth}\left(\frac{{tanu}}{\sqrt{\mathrm{3}}\:}\right)\:+\:{c} \\ $$$${Finally}\:{we}\:{get} \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:{argth}\left(\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\sqrt{\mathrm{3}}}\right)\:+\:{k}\:\:\:\: \\ $$$$ \\ $$

Answered by Rio Michael last updated on 17/Aug/19

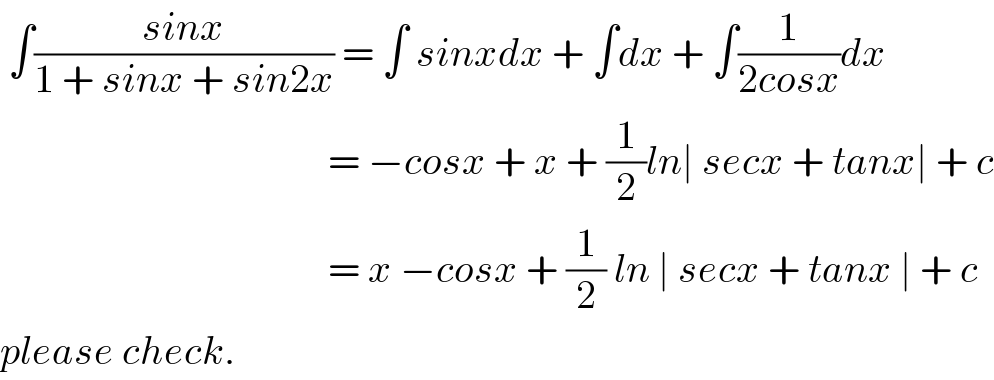
∫((sinx)/(1 + sinx + sin2x)) = ∫ sinxdx + ∫dx + ∫(1/(2cosx))dx = −cosx + x + (1/2)ln∣ secx + tanx∣ + c = x −cosx + (1/2) ln ∣ secx + tanx ∣ + c please check.

$$\:\int\frac{{sinx}}{\mathrm{1}\:+\:{sinx}\:+\:{sin}\mathrm{2}{x}}\:=\:\int\:{sinxdx}\:+\:\int{dx}\:+\:\int\frac{\mathrm{1}}{\mathrm{2}{cosx}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−{cosx}\:+\:{x}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\:{secx}\:+\:{tanx}\mid\:+\:{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{x}\:−{cosx}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:{ln}\:\mid\:{secx}\:+\:{tanx}\:\mid\:+\:{c} \\ $$$${please}\:{check}. \\ $$

Commented by mr W last updated on 17/Aug/19

totally wrong sir! (a/(x+y+z))≠(a/x)+(a/y)+(a/z) !

$${totally}\:{wrong}\:{sir}! \\ $$$$\frac{{a}}{{x}+{y}+{z}}\neq\frac{{a}}{{x}}+\frac{{a}}{{y}}+\frac{{a}}{{z}}\:! \\ $$

Commented by MJS last updated on 17/Aug/19

wrong. learn the laws of calculating with fractiond (a/(a+b))≠(a/b)+(a/c) (a/b)+(a/c)=((ac)/(bc))+((ab)/(bc))=((a(b+c))/(bc)) how could this be true: (5/6)=(5/(5+1))=(5/5)+(5/1)=1+5=6 but (5/6)=(5/(2+4))=(5/2)+(5/4)=((15)/4) and (5/6)=(5/(3+3))=(5/3)+(5/3)=((10)/3) ⇒^? (5/6)=6=((15)/4)=((10)/3)

$$\mathrm{wrong}.\:\mathrm{learn}\:\mathrm{the}\:\mathrm{laws}\:\mathrm{of}\:\mathrm{calculating}\:\mathrm{with}\:\mathrm{fractiond} \\ $$$$\frac{{a}}{{a}+{b}}\neq\frac{{a}}{{b}}+\frac{{a}}{{c}} \\ $$$$\frac{{a}}{{b}}+\frac{{a}}{{c}}=\frac{{ac}}{{bc}}+\frac{{ab}}{{bc}}=\frac{{a}\left({b}+{c}\right)}{{bc}} \\ $$$$\mathrm{how}\:\mathrm{could}\:\mathrm{this}\:\mathrm{be}\:\mathrm{true}:\:\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{5}+\mathrm{1}}=\frac{\mathrm{5}}{\mathrm{5}}+\frac{\mathrm{5}}{\mathrm{1}}=\mathrm{1}+\mathrm{5}=\mathrm{6}\:\mathrm{but} \\ $$$$\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{2}+\mathrm{4}}=\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{4}}=\frac{\mathrm{15}}{\mathrm{4}}\:\mathrm{and}\:\frac{\mathrm{5}}{\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{3}+\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{3}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$$\overset{?} {\Rightarrow}\:\frac{\mathrm{5}}{\mathrm{6}}=\mathrm{6}=\frac{\mathrm{15}}{\mathrm{4}}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$

Commented by Cmr 237 last updated on 17/Aug/19

Answered by Cmr 237 last updated on 17/Aug/19

Commented by MJS last updated on 17/Aug/19

you simply typed this into a solver. but can you explain what happened along the path?

$$\mathrm{you}\:\mathrm{simply}\:\mathrm{typed}\:\mathrm{this}\:\mathrm{into}\:\mathrm{a}\:\mathrm{solver}.\:\mathrm{but}\:\mathrm{can} \\ $$$$\mathrm{you}\:\mathrm{explain}\:\mathrm{what}\:\mathrm{happened}\:\mathrm{along}\:\mathrm{the}\:\mathrm{path}? \\ $$

Commented by mathmax by abdo last updated on 18/Aug/19

this solution is not correct.

$${this}\:{solution}\:{is}\:{not}\:{correct}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com