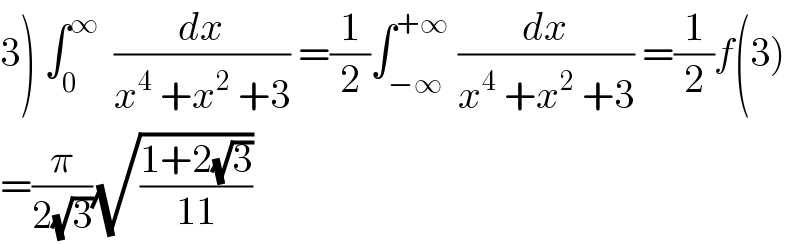Question and Answers Forum
Question Number 66694 by mathmax by abdo last updated on 18/Aug/19
,+∞[ 1) calculate f(a) 2)find also g(a) =∫_(−∞) ^(+∞) (dx/((x^4 +x^2 +a)^2 )) 3) find the value of integrals ∫_0 ^∞ (dx/((x^4 +x^2 +3))) and ∫_0 ^∞ (dx/((x^4 +x^2 +1)^2 )) 4) developp f at integrserie.](Q66694.png)
Commented by mathmax by abdo last updated on 19/Aug/19

Commented by mathmax by abdo last updated on 19/Aug/19
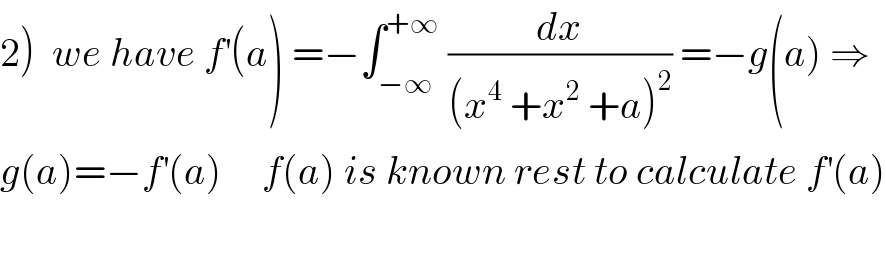
Commented by mathmax by abdo last updated on 19/Aug/19