Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 6672 by FilupSmith last updated on 11/Jul/16

If you pick two random points on a circle′s circumference with radius 1, what is the average area between the two points and the origin?

$$\mathrm{If}\:\mathrm{you}\:\mathrm{pick}\:\mathrm{two}\:\mathrm{random}\:\mathrm{points}\:\mathrm{on}\:\mathrm{a}\:\mathrm{circle}'\mathrm{s} \\ $$$$\mathrm{circumference}\:\mathrm{with}\:\mathrm{radius}\:\mathrm{1},\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{average}\:\mathrm{area}\:\mathrm{between}\:\mathrm{the} \\ $$$$\mathrm{two}\:\mathrm{points}\:\mathrm{and}\:\mathrm{the}\:\mathrm{origin}? \\ $$

Commented by Yozzii last updated on 11/Jul/16

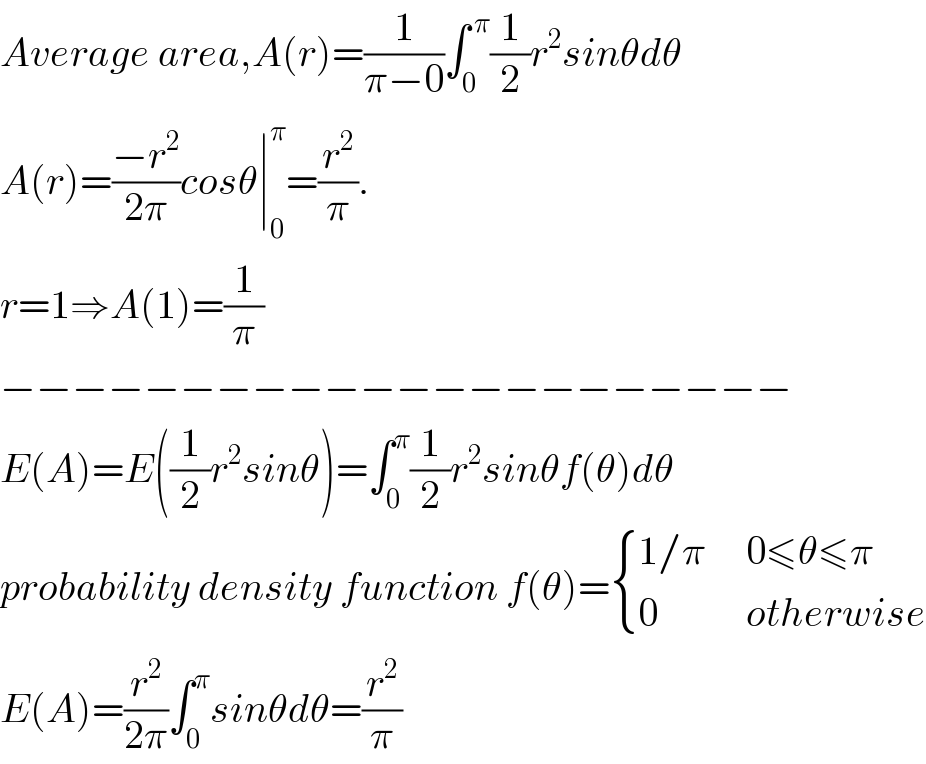
Average area,A(r)=(1/(π−0))∫_0 ^( π) (1/2)r^2 sinθdθ A(r)=((−r^2 )/(2π))cosθ∣_0 ^π =(r^2 /π). r=1⇒A(1)=(1/π) −−−−−−−−−−−−−−−−−−−−−− E(A)=E((1/2)r^2 sinθ)=∫_0 ^π (1/2)r^2 sinθf(θ)dθ probability density function f(θ)= { ((1/π 0≤θ≤π)),((0 otherwise)) :} E(A)=(r^2 /(2π))∫_0 ^π sinθdθ=(r^2 /π)

$${Average}\:{area},{A}\left({r}\right)=\frac{\mathrm{1}}{\pi−\mathrm{0}}\int_{\mathrm{0}} ^{\:\pi} \frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} {sin}\theta{d}\theta \\ $$$${A}\left({r}\right)=\frac{−{r}^{\mathrm{2}} }{\mathrm{2}\pi}{cos}\theta\mid_{\mathrm{0}} ^{\pi} =\frac{{r}^{\mathrm{2}} }{\pi}. \\ $$$${r}=\mathrm{1}\Rightarrow{A}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\pi} \\ $$$$−−−−−−−−−−−−−−−−−−−−−− \\ $$$${E}\left({A}\right)={E}\left(\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} {sin}\theta\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} {sin}\theta{f}\left(\theta\right){d}\theta \\ $$$${probability}\:{density}\:{function}\:{f}\left(\theta\right)=\begin{cases}{\mathrm{1}/\pi\:\:\:\:\:\mathrm{0}\leqslant\theta\leqslant\pi}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:{otherwise}}\end{cases} \\ $$$${E}\left({A}\right)=\frac{{r}^{\mathrm{2}} }{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\pi} {sin}\theta{d}\theta=\frac{{r}^{\mathrm{2}} }{\pi} \\ $$

Commented by FilupSmith last updated on 11/Jul/16

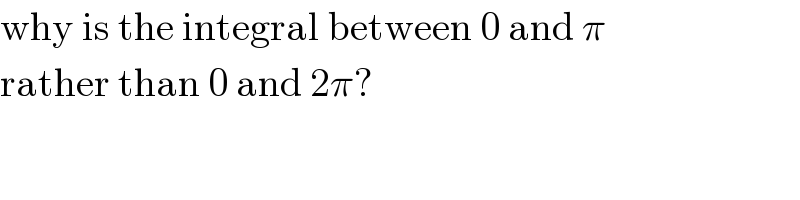
why is the integral between 0 and π rather than 0 and 2π?

$$\mathrm{why}\:\mathrm{is}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{between}\:\mathrm{0}\:\mathrm{and}\:\pi \\ $$$$\mathrm{rather}\:\mathrm{than}\:\mathrm{0}\:\mathrm{and}\:\mathrm{2}\pi? \\ $$

Commented by Yozzii last updated on 11/Jul/16

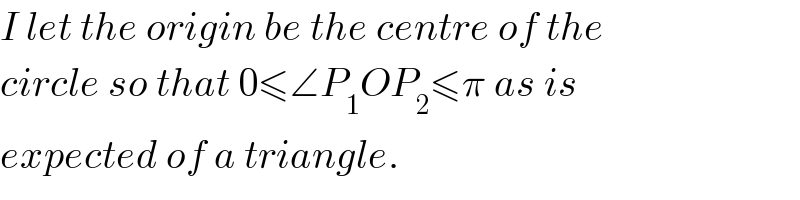
I let the origin be the centre of the circle so that 0≤∠P_1 OP_2 ≤π as is expected of a triangle.

$${I}\:{let}\:{the}\:{origin}\:{be}\:{the}\:{centre}\:{of}\:{the} \\ $$$${circle}\:{so}\:{that}\:\mathrm{0}\leqslant\angle{P}_{\mathrm{1}} {OP}_{\mathrm{2}} \leqslant\pi\:{as}\:{is} \\ $$$${expected}\:{of}\:{a}\:{triangle}. \\ $$

Commented by FilupSmith last updated on 11/Jul/16

I understand! Thanks

$${I}\:{understand}!\:\boldsymbol{{Thanks}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com