Question Number 66728 by Tony Lin last updated on 19/Aug/19
$$\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{x}\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}=? \\ $$
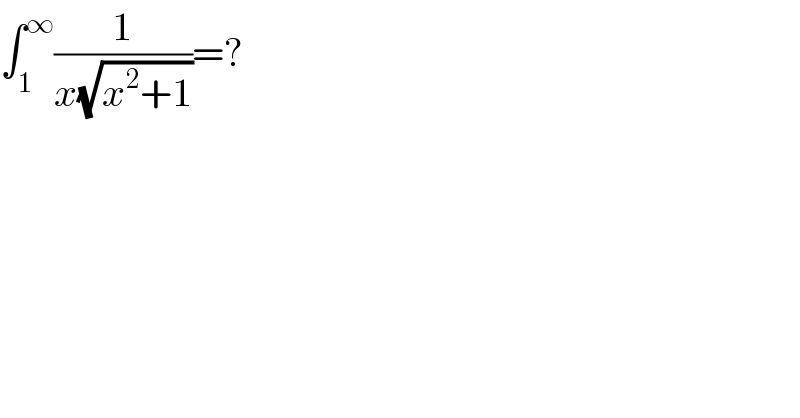
Commented by mathmax by abdo last updated on 19/Aug/19
![changement x=sht give ∫_1 ^(+∞) (dx/(x(√(1+x^2 )))) =∫_(argsh(1)) ^(+∞) ((ch(t)dt)/(sh(t)ch(t))) =2∫_(ln(1+(√2))) ^(+∞) (dt/(e^t −e^(−t) )) =_(e^t =u) 2 ∫_(1+(√2)) ^(+∞) (1/(u−u^(−1) ))(du/u) =2 ∫_(1+(√2)) ^(+∞) (du/(u^2 −1)) =∫_(1+(√2)) ^(+∞) {(1/(u−1))−(1/(u+1))}du=[ln∣((u−1)/(u+1))∣]_(1+(√2)) ^(+∞) =−ln∣((1+(√2)−1)/(1+(√2)+1))∣ =−ln(((√2)/(2+(√2))))=ln(((2+(√2))/(√2))) =ln(1+(√2))](Q66741.png)
$${changement}\:{x}={sht}\:{give}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:=\int_{{argsh}\left(\mathrm{1}\right)} ^{+\infty} \:\:\frac{{ch}\left({t}\right){dt}}{{sh}\left({t}\right){ch}\left({t}\right)} \\ $$$$=\mathrm{2}\int_{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} ^{+\infty} \:\:\frac{{dt}}{{e}^{{t}} −{e}^{−{t}} }\:=_{{e}^{{t}} ={u}} \:\:\:\:\:\mathrm{2}\:\int_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \:\:\frac{\mathrm{1}}{{u}−{u}^{−\mathrm{1}} }\frac{{du}}{{u}} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \:\:\frac{{du}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\int_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \left\{\frac{\mathrm{1}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right\}{du}=\left[{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \\ $$$$=−{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}+\mathrm{1}}\mid\:=−{ln}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)={ln}\left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}}\right)\:={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Commented by Tony Lin last updated on 19/Aug/19
$${thanks}\:{sir} \\ $$
Answered by Souvik Ghosh last updated on 19/Aug/19
![⇔let x=tan Θ⇔dx=sec^2 Θ.dΘ so I=∫_(π/4) ^(π/2) ((sec^2 ΘdΘ)/(tanΘ×sec Θ)) I=∫_(π/4) ^(π/2) cosec Θ dΘ I=−ln[(√2)−1]](Q66729.png)
$$\Leftrightarrow\mathrm{let}\:\:\:\mathrm{x}=\mathrm{tan}\:\Theta\Leftrightarrow\mathrm{dx}=\mathrm{sec}\:^{\mathrm{2}} \Theta.\mathrm{d}\Theta \\ $$$$\mathrm{so}\:\:\mathrm{I}=\int_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \frac{\mathrm{sec}^{\mathrm{2}} \Theta\mathrm{d}\Theta}{\mathrm{tan}\Theta×\mathrm{sec}\:\Theta} \\ $$$$\:\:\:\:\:\mathrm{I}=\int_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \mathrm{cosec}\:\Theta\:\mathrm{d}\Theta \\ $$$$\:\:\:\:\:\:\mathrm{I}=−\mathrm{ln}\left[\sqrt{\mathrm{2}}−\mathrm{1}\right] \\ $$$$\:\:\:\:\:\: \\ $$
Answered by Souvik Ghosh last updated on 19/Aug/19
![⇔let x=tan Θ⇔dx=sec^2 Θ.dΘ so I=∫_(π/4) ^(π/2) ((sec^2 ΘdΘ)/(tanΘ×sec Θ)) I=∫_(π/4) ^(π/2) cosec Θ dΘ I=−ln[(√2)−1]](Q66730.png)
$$\Leftrightarrow\mathrm{let}\:\:\:\mathrm{x}=\mathrm{tan}\:\Theta\Leftrightarrow\mathrm{dx}=\mathrm{sec}\:^{\mathrm{2}} \Theta.\mathrm{d}\Theta \\ $$$$\mathrm{so}\:\:\mathrm{I}=\int_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \frac{\mathrm{sec}^{\mathrm{2}} \Theta\mathrm{d}\Theta}{\mathrm{tan}\Theta×\mathrm{sec}\:\Theta} \\ $$$$\:\:\:\:\:\mathrm{I}=\int_{\pi/\mathrm{4}} ^{\pi/\mathrm{2}} \mathrm{cosec}\:\Theta\:\mathrm{d}\Theta \\ $$$$\:\:\:\:\:\:\mathrm{I}=−\mathrm{ln}\left[\sqrt{\mathrm{2}}−\mathrm{1}\right] \\ $$$$\:\:\:\:\:\: \\ $$
Commented by Tony Lin last updated on 19/Aug/19
$${thanks}\:{sir} \\ $$