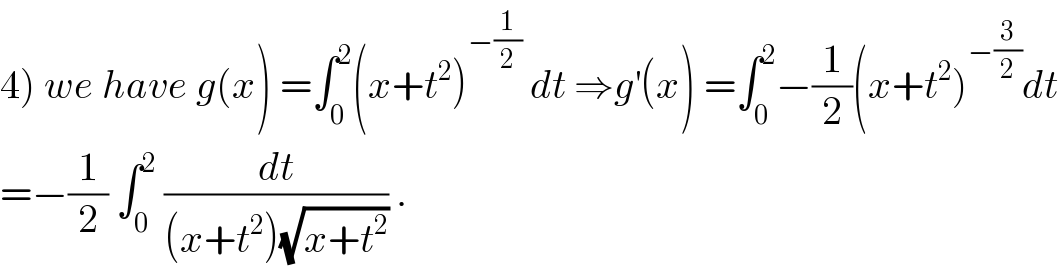Question and Answers Forum
Question Number 66801 by mathmax by abdo last updated on 19/Aug/19
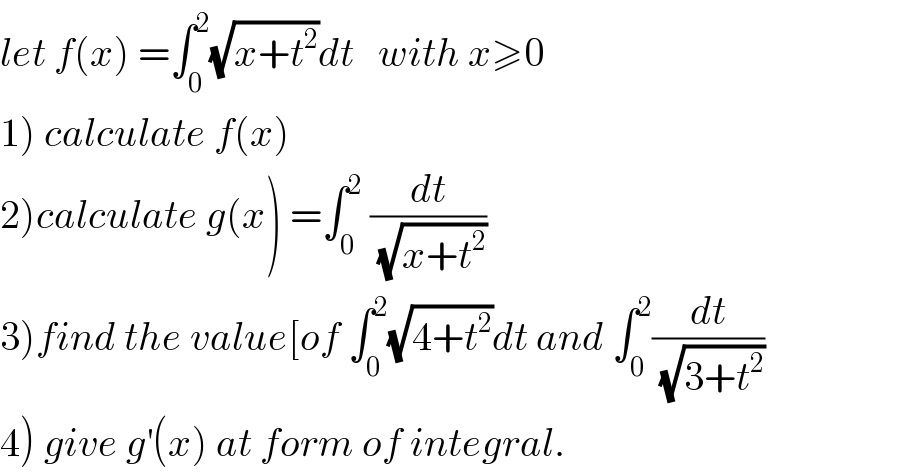
Commented by mathmax by abdo last updated on 21/Aug/19
![1) f(x)=∫_0 ^2 (√(x+t^2 ))dt changement t =(√x)u give f(x)=∫_0 ^(2/(√x)) (√x)(√(1+u^2 ))(√x)du =x ∫_0 ^(2/(√x)) (√(1+u^2 ))du changement u=shz give f(x) =x ∫_0 ^(argsh((2/(√x)))) ch(z)ch(z)ez =(x/2) ∫_0 ^(argsh((2/((√)x)))) (ch(2z)+1)dz =(x/4)[sh(2z)]_0 ^(ln((2/(√x))+(√(1+(4/x))))) +(x/2)ln((2/(√x))+(√(1+(4/x)))) =(x/8)[e^(2z) −e^(−2z) ]_0 ^(ln(((2+(√(x+4)))/((√x) )))) +(x/2)ln(((2+(√(x+4)))/(√x))) ⇒ f(x)=(x/8){(((2+(√(x+4)))/(√x)))^2 −(1/((((2+(√(x+4)))/(√x)))^2 ))}+(x/2)ln(((2+(√(x+4)))/(√x))) 2)we have f^′ (x)= ∫_0 ^2 (1/(2(√(x+t^2 )))) dt =(1/2)g(x) ⇒g(x) =2f^′ (x) rest to calculate f^′ (x) ..be continued...](Q66940.png)
Commented by mathmax by abdo last updated on 21/Aug/19
![3) we have ∫_0 ^2 (√(4+t^2 ))dt =f(4) =(1/2){(((2+2(√2))/2))^2 −(1/((((2+2(√2))/2))^2 )) +2ln(((2+2(√2))/2)) =(1/2){ (1+(√2))^2 −(1/((1+(√2))^2 ))} +2ln(1+(√2)) ∫_0 ^2 (dt/(√(3+t^2 ))) =_(t=(√3)u) ∫_0 ^(2/(√3)) (((√3)du)/((√3)(√(1+u^2 )))) =∫_0 ^(2/(√3)) (du/(√(1+u^2 ))) =[ln(u+(√(1+u^2 )))]_0 ^(2/(√3)) =ln((2/(√3)) +(√(1+(4/3)))) =ln(((2+(√7))/(√3)))](Q66941.png)
Commented by mathmax by abdo last updated on 21/Aug/19