Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 67013 by mathmax by abdo last updated on 21/Aug/19

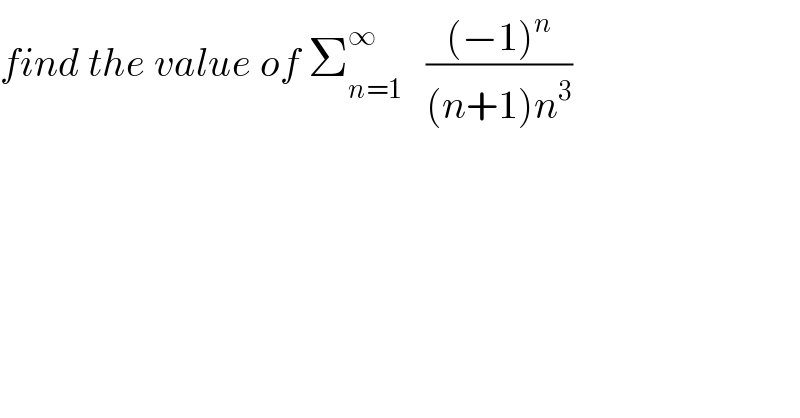
find the value of Σ_(n=1) ^∞ (((−1)^n )/((n+1)n^3 ))

$${find}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right){n}^{\mathrm{3}} } \\ $$

Commented by mathmax by abdo last updated on 24/Aug/19

let S =Σ_(n=1) ^∞ (((−1)^n )/((n+1)n^3 )) we have S =lim_(n→+∞) S_n with S_n =Σ_(k=1) ^n (((−1)^k )/((k+1)k^3 )) let first decompose F(x) =(1/((x+1)x^3 )) F(x)=(a/(x+1))+(b/x) +(c/x^2 ) +(d/x^3 ) we have a =−1 d =1 ⇒F(x) =−(1/(x+1)) +(b/x)+(c/x^2 ) +(1/x^3 ) lim_(x→+∞) xF(x) =0 =−1+b ⇒b=1 ⇒F(x)=−(1/(x+1))+(1/x) +(c/x^2 ) +(1/x^3 ) F(1)=(1/2) =−(1/2) +2+c ⇒1 =2+c ⇒c =−1 ⇒ F(x)=−(1/(x+1))+(1/x)−(1/x^2 )+(1/x^3 ) ⇒S_n =Σ_(k=1) ^n (−1)^k F(k) =−Σ_(k=1) ^n (((−1)^k )/(k+1)) +Σ_(k=1) ^n (((−1)^k )/k)−Σ_(k=1) ^n (((−1)^k )/k^2 ) +Σ_(k=1) ^n (((−1)^k )/k^3 ) but Σ_(k=1) ^n (((−1)^k )/(k+1)) =Σ_(k=2) ^(n+1) (((−1)^(k−1) )/k) =−Σ_(k=2) ^(n+1) (((−1)^k )/k) =−(Σ_(k=1) ^(n+1) (((−1)^k )/k)+1)=1−Σ_(k=1) ^(n+1) (((−1)^k )/k) ⇒ S_n =−1 +Σ_(k=1) ^(n+1) (((−1)^k )/k) +Σ_(k=1) ^∞ (((−1)^k )/k)−Σ_(k=1) ^n (((−1)^k )/k^2 )+Σ_(k=1) ^n (((−1)^k )/k^3 ) → −1+2Σ_(k=1) ^∞ (((−1)^k )/k) −Σ_(k=1) ^∞ (((−1)^k )/k^2 ) +Σ_(k=1) ^∞ (((−1)^k )/k^3 ) we have Σ_(k=1) ^∞ (((−1)^k )/k) =−ln(2) Σ_(k=1) ^∞ (((−1)^k )/k^x ) =δ(x)=(2^(1−x) −1)ξ(x) ⇒ Σ_(k=1) ^∞ (((−1)^k )/k^2 ) =(2^(−1) −1)ξ(2) =−(1/2)×(π^2 /6) =−(π^2 /(12)) Σ_(k=1) ^∞ (((−1)^k )/k^3 ) =(2^(1−3) −1)ξ(3) =−(3/4)ξ(3) ⇒ S =lim_(n→+∞) S_n =−1+2(−ln(2))+(π^2 /(12))−(3/4)ξ(3) =(π^2 /(12))−1−2ln(2)−(3/4)ξ(3) .

$${let}\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right){n}^{\mathrm{3}} }\:{we}\:{have}\:{S}\:={lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \:{with}\: \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}+\mathrm{1}\right){k}^{\mathrm{3}} }\:\:{let}\:\:{first}\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right){x}^{\mathrm{3}} } \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}+\mathrm{1}}+\frac{{b}}{{x}}\:+\frac{{c}}{{x}^{\mathrm{2}} }\:+\frac{{d}}{{x}^{\mathrm{3}} }\:\:{we}\:{have}\:{a}\:=−\mathrm{1} \\ $$$${d}\:=\mathrm{1}\:\Rightarrow{F}\left({x}\right)\:=−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{{b}}{{x}}+\frac{{c}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{0}\:=−\mathrm{1}+{b}\:\Rightarrow{b}=\mathrm{1}\:\Rightarrow{F}\left({x}\right)=−\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}}\:+\frac{{c}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{2}+{c}\:\Rightarrow\mathrm{1}\:=\mathrm{2}+{c}\:\Rightarrow{c}\:=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(−\mathrm{1}\right)^{{k}} \:{F}\left({k}\right) \\ $$$$=−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\mathrm{1}}\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{2}} }\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{k}}} }{\boldsymbol{{k}}^{\mathrm{3}} } \\ $$$$\boldsymbol{{but}}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\mathrm{1}}\:=\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}\:=−\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$$=−\left(\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}+\mathrm{1}\right)=\mathrm{1}−\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:\Rightarrow \\ $$$${S}_{{n}} =−\mathrm{1}\:+\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:+\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}−\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{2}} }+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{3}} } \\ $$$$\rightarrow\:−\mathrm{1}+\mathrm{2}\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:−\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{2}} }\:+\sum_{{k}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{3}} } \\ $$$${we}\:{have}\:\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:=−{ln}\left(\mathrm{2}\right) \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{{x}} }\:=\delta\left({x}\right)=\left(\mathrm{2}^{\mathrm{1}−{x}} −\mathrm{1}\right)\xi\left({x}\right)\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{2}} }\:=\left(\mathrm{2}^{−\mathrm{1}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{3}} }\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{3}} −\mathrm{1}\right)\xi\left(\mathrm{3}\right)\:=−\frac{\mathrm{3}}{\mathrm{4}}\xi\left(\mathrm{3}\right)\:\Rightarrow \\ $$$${S}\:={lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =−\mathrm{1}+\mathrm{2}\left(−{ln}\left(\mathrm{2}\right)\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{3}}{\mathrm{4}}\xi\left(\mathrm{3}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\mathrm{1}−\mathrm{2}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{3}}{\mathrm{4}}\xi\left(\mathrm{3}\right)\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com