Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 6710 by Tawakalitu. last updated on 15/Jul/16

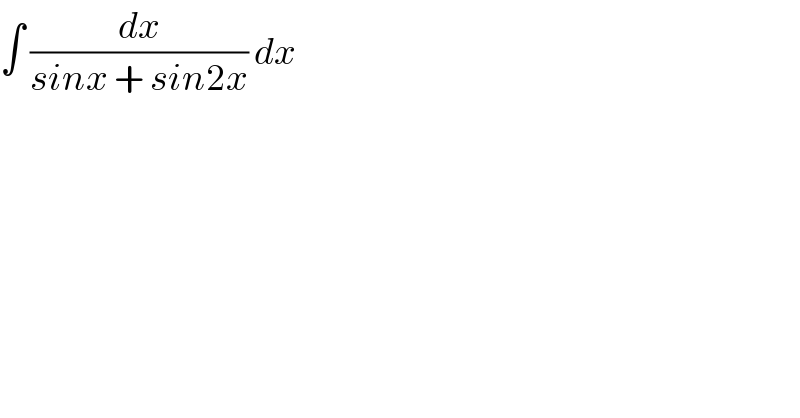
∫ (dx/(sinx + sin2x)) dx

$$\int\:\frac{{dx}}{{sinx}\:+\:{sin}\mathrm{2}{x}}\:{dx} \\ $$

Answered by Yozzii last updated on 15/Jul/16

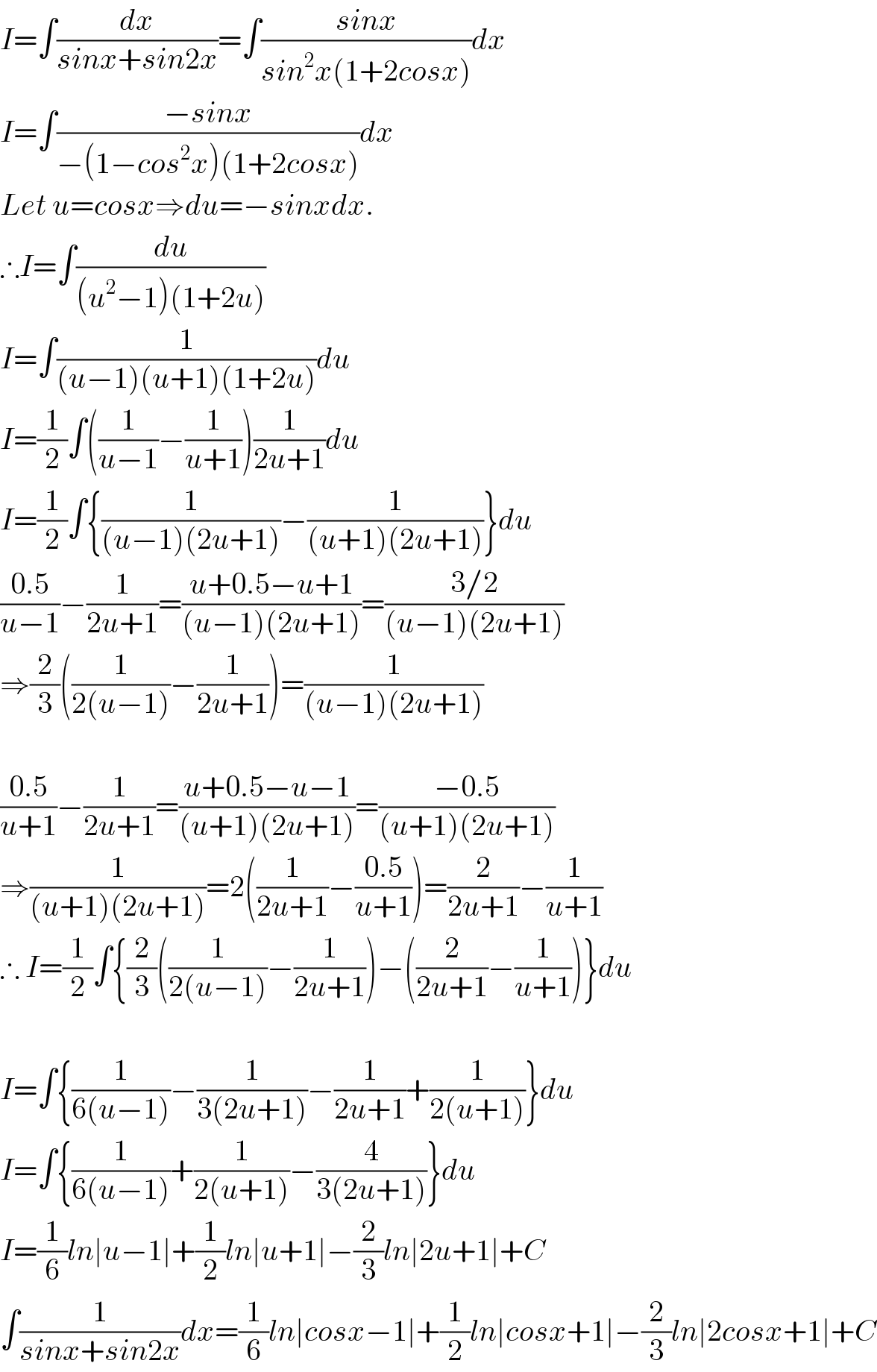
I=∫(dx/(sinx+sin2x))=∫((sinx)/(sin^2 x(1+2cosx)))dx I=∫((−sinx)/(−(1−cos^2 x)(1+2cosx)))dx Let u=cosx⇒du=−sinxdx. ∴I=∫(du/((u^2 −1)(1+2u))) I=∫(1/((u−1)(u+1)(1+2u)))du I=(1/2)∫((1/(u−1))−(1/(u+1)))(1/(2u+1))du I=(1/2)∫{(1/((u−1)(2u+1)))−(1/((u+1)(2u+1)))}du ((0.5)/(u−1))−(1/(2u+1))=((u+0.5−u+1)/((u−1)(2u+1)))=((3/2)/((u−1)(2u+1))) ⇒(2/3)((1/(2(u−1)))−(1/(2u+1)))=(1/((u−1)(2u+1))) ((0.5)/(u+1))−(1/(2u+1))=((u+0.5−u−1)/((u+1)(2u+1)))=((−0.5)/((u+1)(2u+1))) ⇒(1/((u+1)(2u+1)))=2((1/(2u+1))−((0.5)/(u+1)))=(2/(2u+1))−(1/(u+1)) ∴ I=(1/2)∫{(2/3)((1/(2(u−1)))−(1/(2u+1)))−((2/(2u+1))−(1/(u+1)))}du I=∫{(1/(6(u−1)))−(1/(3(2u+1)))−(1/(2u+1))+(1/(2(u+1)))}du I=∫{(1/(6(u−1)))+(1/(2(u+1)))−(4/(3(2u+1)))}du I=(1/6)ln∣u−1∣+(1/2)ln∣u+1∣−(2/3)ln∣2u+1∣+C ∫(1/(sinx+sin2x))dx=(1/6)ln∣cosx−1∣+(1/2)ln∣cosx+1∣−(2/3)ln∣2cosx+1∣+C

$${I}=\int\frac{{dx}}{{sinx}+{sin}\mathrm{2}{x}}=\int\frac{{sinx}}{{sin}^{\mathrm{2}} {x}\left(\mathrm{1}+\mathrm{2}{cosx}\right)}{dx} \\ $$$${I}=\int\frac{−{sinx}}{−\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)\left(\mathrm{1}+\mathrm{2}{cosx}\right)}{dx} \\ $$$${Let}\:{u}={cosx}\Rightarrow{du}=−{sinxdx}. \\ $$$$\therefore{I}=\int\frac{{du}}{\left({u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{1}+\mathrm{2}{u}\right)} \\ $$$${I}=\int\frac{\mathrm{1}}{\left({u}−\mathrm{1}\right)\left({u}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{2}{u}\right)}{du} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right)\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}{du} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{1}}{\left({u}−\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({u}+\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)}\right\}{du} \\ $$$$\frac{\mathrm{0}.\mathrm{5}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}=\frac{{u}+\mathrm{0}.\mathrm{5}−{u}+\mathrm{1}}{\left({u}−\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)}=\frac{\mathrm{3}/\mathrm{2}}{\left({u}−\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}\left({u}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\left({u}−\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)} \\ $$$$ \\ $$$$\frac{\mathrm{0}.\mathrm{5}}{{u}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}=\frac{{u}+\mathrm{0}.\mathrm{5}−{u}−\mathrm{1}}{\left({u}+\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)}=\frac{−\mathrm{0}.\mathrm{5}}{\left({u}+\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left({u}+\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)}=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}−\frac{\mathrm{0}.\mathrm{5}}{{u}+\mathrm{1}}\right)=\frac{\mathrm{2}}{\mathrm{2}{u}+\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}} \\ $$$$\therefore\:{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}\left({u}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}\right)−\left(\frac{\mathrm{2}}{\mathrm{2}{u}+\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right)\right\}{du} \\ $$$$ \\ $$$${I}=\int\left\{\frac{\mathrm{1}}{\mathrm{6}\left({u}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2}{u}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}{u}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\left({u}+\mathrm{1}\right)}\right\}{du} \\ $$$${I}=\int\left\{\frac{\mathrm{1}}{\mathrm{6}\left({u}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({u}+\mathrm{1}\right)}−\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{2}{u}+\mathrm{1}\right)}\right\}{du} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{u}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{u}+\mathrm{1}\mid−\frac{\mathrm{2}}{\mathrm{3}}{ln}\mid\mathrm{2}{u}+\mathrm{1}\mid+{C} \\ $$$$\int\frac{\mathrm{1}}{{sinx}+{sin}\mathrm{2}{x}}{dx}=\frac{\mathrm{1}}{\mathrm{6}}{ln}\mid{cosx}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cosx}+\mathrm{1}\mid−\frac{\mathrm{2}}{\mathrm{3}}{ln}\mid\mathrm{2}{cosx}+\mathrm{1}\mid+{C} \\ $$

Commented by Tawakalitu. last updated on 15/Jul/16

Wow thanks so much.

$${Wow}\:{thanks}\:{so}\:{much}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com