
Question and Answers Forum
Question Number 67246 by Learner-123 last updated on 24/Aug/19
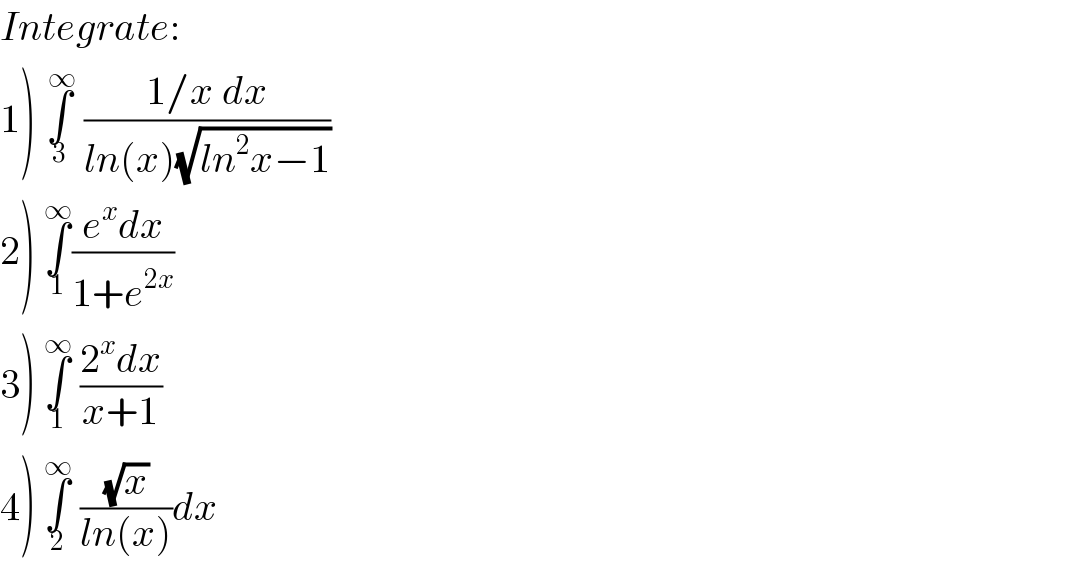
Commented by MJS last updated on 24/Aug/19

Commented by mathmax by abdo last updated on 24/Aug/19
![2) let I =∫_1 ^∞ (e^x /(1+e^(2x) ))dx changement e^x =t give I =∫_e ^(+∞) (t/(1+t^2 ))(dt/t) =∫_e ^(+∞) (dt/(1+t^2 )) =[arctan(t)]_e ^(+∞) =(π/2) −arctan(e).](Q67251.png)
Commented by mathmax by abdo last updated on 24/Aug/19
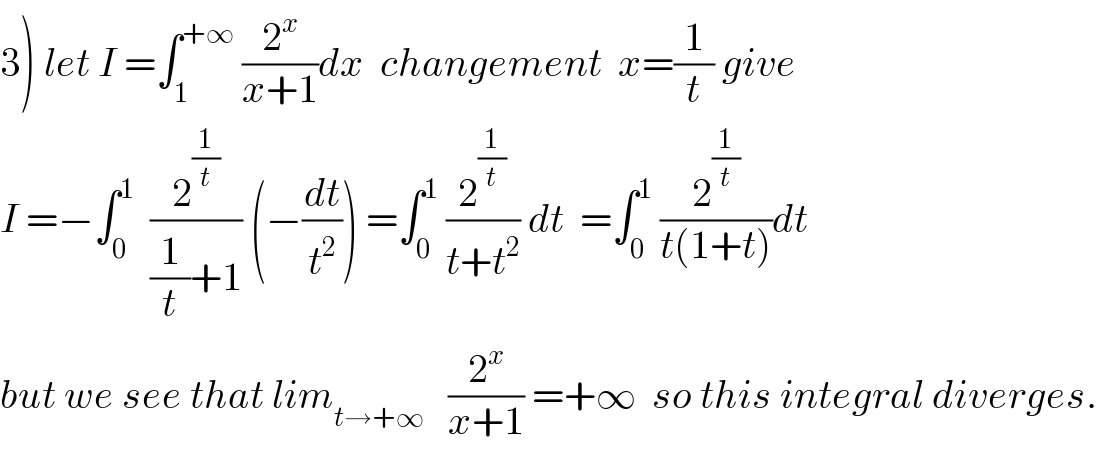
Commented by mathmax by abdo last updated on 24/Aug/19
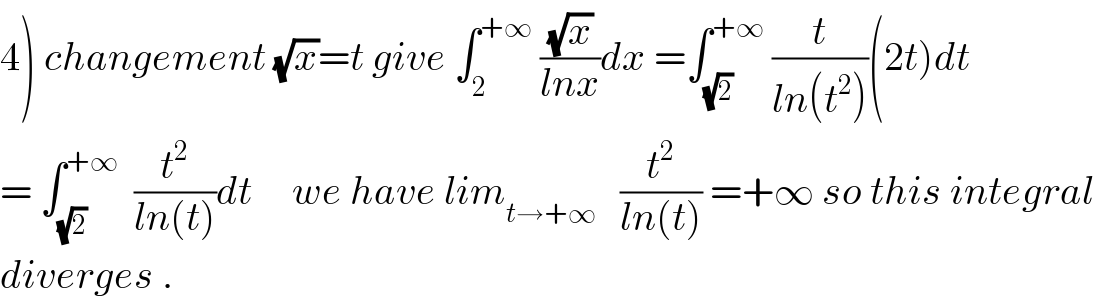
Answered by MJS last updated on 24/Aug/19
![1) ∫(((1/x)dx)/(ln x (√(ln^2 x −1))))= [t=ln x → dx=xdt] =∫(dt/(t(√(t^2 −1))))= [u=(√(t^2 −1)) → dt=((√(t^2 −1))/t)du] =∫(du/(u^2 +1))=arctan u =arctan (√(t^2 −1)) =arctan (√(ln^2 x −1)) +C](Q67247.png)
Commented by MJS last updated on 24/Aug/19
![in one step: ∫(((1/x)dx)/(ln x (√(ln^2 x −1))))= [t=(√(ln^2 x −1)) → dx=((x(√(ln^2 x −1)))/(ln x))] =∫(dt/(t^2 +1))=...](Q67248.png)
Commented by Learner-123 last updated on 25/Aug/19

Answered by MJS last updated on 24/Aug/19
![2) ∫(e^x /(1+e^(2x) ))dx= [t=e^x → dx=(dt/e^x )] =∫(dt/(t^2 +1))=arctan t =arctan e^x +C](Q67249.png)
