
Question Number 67299 by Rio Michael last updated on 25/Aug/19

$${G}\left({x}\right)=\:\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right){Q}\left({x}\right)\:+\:{px}\:+{q} \\ $$$$\left.{a}\right)\:{Given}\:{that}\:{G}\left({x}\right)\:{leaves}\:{a}\:{remainder}\:{of}\:\mathrm{8}\:{and}\:−\mathrm{24}\:{when}\:{divided}\:{by}\:\left({x}+\mathrm{1}\right)\:{and}\: \\ $$$$\left({x}+\mathrm{3}\right)\:{respectively},{find}\:{the}\:{remainder}\:{when}\:{G}\left({x}\right)\:{is}\:{divided}\:{by}\:\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right). \\ $$$$\left.{b}\right)\:\:{Given}\:{that}\:{x}+\mathrm{2}\:{is}\:{a}\:{factor}\:{of}\:{G}\left({x}\right)\:{and}\:{that}\:{the}\:{graph}\:{of}\:{G}\left({x}\right)\:{passes}\:{through} \\ $$$${the}\:{point}\:{with}\:{coordinates}\:\left(\mathrm{0},\mathrm{6}\right)\:{find}\:{G}\left({x}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 28/Aug/19
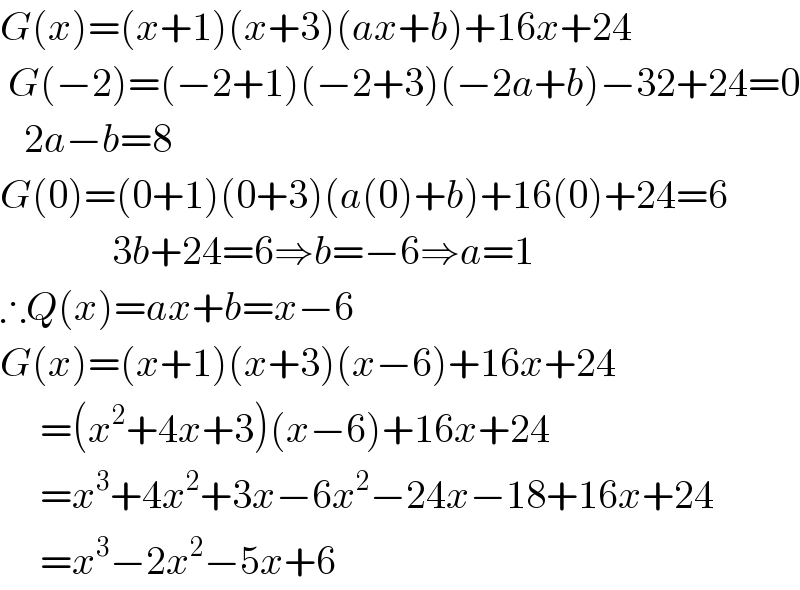
$${G}\left({x}\right)=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({ax}+{b}\right)+\mathrm{16}{x}+\mathrm{24} \\ $$$$\:{G}\left(−\mathrm{2}\right)=\left(−\mathrm{2}+\mathrm{1}\right)\left(−\mathrm{2}+\mathrm{3}\right)\left(−\mathrm{2}{a}+{b}\right)−\mathrm{32}+\mathrm{24}=\mathrm{0} \\ $$$$\:\:\:\mathrm{2}{a}−{b}=\mathrm{8} \\ $$$${G}\left(\mathrm{0}\right)=\left(\mathrm{0}+\mathrm{1}\right)\left(\mathrm{0}+\mathrm{3}\right)\left({a}\left(\mathrm{0}\right)+{b}\right)+\mathrm{16}\left(\mathrm{0}\right)+\mathrm{24}=\mathrm{6}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{b}+\mathrm{24}=\mathrm{6}\Rightarrow{b}=−\mathrm{6}\Rightarrow{a}=\mathrm{1} \\ $$$$\therefore{Q}\left({x}\right)={ax}+{b}={x}−\mathrm{6} \\ $$$${G}\left({x}\right)=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({x}−\mathrm{6}\right)+\mathrm{16}{x}+\mathrm{24} \\ $$$$\:\:\:\:\:=\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}\right)\left({x}−\mathrm{6}\right)+\mathrm{16}{x}+\mathrm{24} \\ $$$$\:\:\:\:\:={x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{6}{x}^{\mathrm{2}} −\mathrm{24}{x}−\mathrm{18}+\mathrm{16}{x}+\mathrm{24} \\ $$$$\:\:\:\:\:={x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6} \\ $$
Commented by Rasheed.Sindhi last updated on 28/Aug/19

$${Sir}\:{mr}\:{W}!\:{I}\:{made}\:{my}\:{answer}\:{more} \\ $$$${compact}\:{in}\:{the}\:{light}\:{of}\:{your}\:{comment}. \\ $$$${However}\:{its}\:{only}\:'{unique}\:{cubic}\:{solution}'. \\ $$
Commented by Rasheed.Sindhi last updated on 29/Aug/19

$$\:{mr}\:{W}\:{sir},\:{Can}\:{we}\:{translate}\:{the}\:{problem}\:\:\:\: \\ $$$${as}\:{follows}:\:\left({I}'{ve}\:{seen}\:{great}\:{resemblance}\:{between}\right. \\ $$$${this}\:{problem}\:\&\:{Q}#\mathrm{66832}\:\left({with}\:{ans}\:\mathrm{1731}\right) \\ $$$$\:\:\:\:\:\:{G}\left({x}\right)\equiv\mathrm{8}\left({mod}\:\left({x}+\mathrm{1}\right)\:\right) \\ $$$$\:\:\:\:\:\:{G}\left({x}\right)\equiv−\mathrm{24}\left({mod}\:\left({x}+\mathrm{3}\right)\:\right) \\ $$$$\:\:\:\:\:\:{G}\left({x}\right)\equiv\mathrm{0}\left({mod}\:\left({x}+\mathrm{2}\right)\:\:\right) \\ $$$$\:\:\:\:\:\:{G}\left({x}\right)\equiv\mathrm{6}\left({mod}\:{x}\:\:\right) \\ $$
Commented by mr W last updated on 29/Aug/19
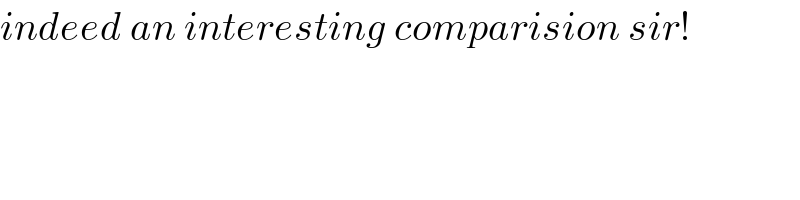
$${indeed}\:{an}\:{interesting}\:{comparision}\:{sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 02/Sep/19
Sir mr W, I've tried to solve the above problem using Chinese Remainder Theorm.Pl see Q#67697.
Answered by Rasheed.Sindhi last updated on 26/Aug/19

$${a} \\ $$$${If}\:{any}\:{polynomial}\:{P}\left({x}\right)\:{is}\:{divided}\:{by} \\ $$$${an}\:{other}\:{polynomial}\:{D}\left({x}\right)\:{giving}\:{quotient} \\ $$$${Q}\left({x}\right)\:{and}\:{remainder}\:{R}\left({x}\right),{then} \\ $$$${P}\left({x}\right)={D}\left({x}\right)×{Q}\left({x}\right)+{R}\left({x}\right)\:{where}\:{R}\left({x}\right) \\ $$$${is}\:{lower}\:{in}\:{degree}\:{than}\:{D}\left({x}\right). \\ $$$${Now}\:{in} \\ $$$${G}\left({x}\right)=\:\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right){Q}\left({x}\right)\:+\:{px}\:+{q} \\ $$$${if}\:\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\:{is}\:{divisor}\:{having}\:{degree} \\ $$$$\mathrm{2},\:{then}\:{surely}\:{px}+{q}\:{having}\:{degree}\:\mathrm{1} \\ $$$$\left({lower}\:{than}\:{that}\:{of}\:{divisor}\right)\:{is}\:{remainder}. \\ $$$${Now}\:{the}\:{work}\:{remained}\:{is}\:{only}\:{to} \\ $$$${determine}\:{values}\:{of}\:{p}\:\&\:{q}\:{if}\:{we}\:{could} \\ $$$${determine}. \\ $$$$\:^{\bullet} {G}\left({x}\right)\:{is}\:{divided}\:{by}\:{x}+\mathrm{1}\:{giving}\: \\ $$$${remainder}\:\mathrm{8}: \\ $$$$\:\therefore{G}\left(−\mathrm{1}\right)=\mathrm{8} \\ $$$${p}\left(−\mathrm{1}\right)+{q}=\mathrm{8}\Rightarrow{p}−{q}=−\mathrm{8}.........\left({i}\right) \\ $$$$\:^{\bullet} {G}\left({x}\right)\:{is}\:{divided}\:{by}\:{x}+\mathrm{3}\:{giving}\: \\ $$$${remainder}\:−\mathrm{24}: \\ $$$$\therefore\:{p}\left(−\mathrm{3}\right)+{q}=−\mathrm{24}\Rightarrow\mathrm{3}{p}−{q}=\mathrm{24}.......\left({ii}\right) \\ $$$$\left({ii}\right)−\left({i}\right):\mathrm{2}{p}=\mathrm{32}\Rightarrow{p}=\mathrm{16} \\ $$$${p}−{q}=−\mathrm{8}\Rightarrow\mathrm{16}−{q}=−\mathrm{8}\Rightarrow{q}=\mathrm{24} \\ $$$$\therefore\:\:{The}\:{required}\:{remainder}: \\ $$$$\:\:\:\:\:\:\:{px}+{q}=\mathrm{16}{x}+\mathrm{24} \\ $$
Commented by Rio Michael last updated on 27/Aug/19

$${thank}\:{you}\:{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 27/Aug/19

$${b} \\ $$$${G}\left(−\mathrm{1}\right)=\mathrm{8} \\ $$$${G}\left(−\mathrm{3}\right)=−\mathrm{24} \\ $$$${G}\left(−\mathrm{2}\right)=\mathrm{0} \\ $$$${G}\left(\mathrm{0}\right)=\mathrm{6} \\ $$$${G}\left({x}\right)\:{at}\:{least}\:{quadratic}. \\ $$$${G}\left({x}\right)=? \\ $$$$\bullet{Let}\:{G}\left({x}\right)=\left({x}+\mathrm{2}\right)\left({ax}+{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ax}^{\mathrm{2}} +\left({b}+\mathrm{2}{a}\right){x}+\mathrm{2}{b} \\ $$$${G}\left(\mathrm{0}\right)=\mathrm{6}\Rightarrow\mathrm{2}{b}=\mathrm{6}\Rightarrow{b}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:{G}\left({x}\right)={ax}^{\mathrm{2}} +\left(\mathrm{2}{a}+\mathrm{3}\right){x}+\mathrm{6} \\ $$$$\begin{pmatrix}{\left.−\mathrm{1}\right)}&{{a}}&{\mathrm{2}{a}+\mathrm{3}}&{\:\:\:\:\:\:\:\:\:\mathrm{6}}\\{}&{}&{−{a}}&{\:\:\:\:−{a}−\mathrm{3}}\\{}&{{a}}&{{a}+\mathrm{3}}&{−{a}+\mathrm{3}=\mathrm{8}}\end{pmatrix}\: \\ $$$$−{a}+\mathrm{3}=\mathrm{8}\Rightarrow{a}=−\mathrm{5} \\ $$$${G}\left({x}\right)=−\mathrm{5}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{6} \\ $$$$ \\ $$$$\begin{pmatrix}{\left.−\mathrm{3}\right)}&{−\mathrm{5}}&{−\mathrm{7}}&{\:\:\:\:\:\:\:\:\:\mathrm{6}}\\{}&{}&{\mathrm{15}}&{\:\:\:\:−\mathrm{24}}\\{}&{−\mathrm{5}}&{\:\:\mathrm{8}}&{\:\:\:\:\:\:\:−\mathrm{18}}\end{pmatrix}\: \\ $$$${G}\left(−\mathrm{3}\right)=−\mathrm{18} \\ $$$${This}\:{is}\:{against}\:{to}\:{the}\:{given}\left({G}\left(−\mathrm{3}\right)=−\mathrm{24}\right. \\ $$$$\:\therefore{G}\left({x}\right)\neq\left({x}+\mathrm{2}\right)\left({ax}+{b}\right) \\ $$$$ \\ $$$$\bullet{Let}\:{G}\left({x}\right)=\left({x}+\mathrm{2}\right)\left({ax}^{\mathrm{2}} +{bx}+{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+\mathrm{2}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+\mathrm{2}{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={ax}^{\mathrm{3}} +\mathrm{2}{ax}^{\mathrm{2}} +{bx}^{\mathrm{2}} +\mathrm{2}{bx}+{cx}+\mathrm{2}{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={ax}^{\mathrm{3}} +\left(\mathrm{2}{a}+{b}\right){x}^{\mathrm{2}} +\left(\mathrm{2}{b}+{c}\right){x}+\mathrm{2}{c} \\ $$$${G}\left(\mathrm{0}\right)=\mathrm{6}\Rightarrow\mathrm{2}{c}=\mathrm{6}\Rightarrow{c}=\mathrm{3} \\ $$$$\:\:{G}\left({x}\right)={ax}^{\mathrm{3}} +\left(\mathrm{2}{a}+{b}\right){x}^{\mathrm{2}} +\left(\mathrm{2}{b}+\mathrm{3}\right){x}+\mathrm{6} \\ $$$$\begin{pmatrix}{\left.−\mathrm{1}\right)}&{{a}}&{\mathrm{2}{a}+{b}}&{\:\:\:\:\:\mathrm{2}{b}+\mathrm{3}}&{\:\:\:\:\:\mathrm{6}}\\{}&{}&{−{a}}&{\:\:\:−{a}−{b}}&{{a}−{b}−\mathrm{3}}\\{}&{{a}}&{{a}+{b}}&{−{a}+{b}+\mathrm{3}}&{{a}−{b}+\mathrm{3}=\mathrm{8}}\end{pmatrix}\: \\ $$$${a}−{b}=\mathrm{5}\Rightarrow{a}={b}+\mathrm{5} \\ $$$$\begin{pmatrix}{\left.−\mathrm{3}\right)}&{{a}}&{\mathrm{2}{a}+{b}}&{\:\:\:\:\:\mathrm{2}{b}+\mathrm{3}}&{\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}}\\{}&{}&{−\mathrm{3}{a}}&{\:\:\:\mathrm{3}{a}−\mathrm{3}{b}}&{\:\:\:\:\:−\mathrm{9}{a}+\mathrm{3}{b}−\mathrm{9}}\\{}&{{a}}&{−{a}+{b}}&{\mathrm{3}{a}−{b}+\mathrm{3}}&{−\mathrm{9}{a}+\mathrm{3}{b}−\mathrm{3}=−\mathrm{24}}\end{pmatrix}\: \\ $$$$\:\:\:\:\:−\mathrm{9}{a}+\mathrm{3}{b}=−\mathrm{21} \\ $$$$\:\:\:\:−\mathrm{3}{a}+{b}=−\mathrm{7} \\ $$$$\:\:\:\:\:\:\:−\mathrm{3}\left({b}+\mathrm{5}\right)+{b}=−\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:........ \\ $$$$\:\:\:\:\:\:\:−\mathrm{2}{b}=−\mathrm{7}+\mathrm{15}=\mathrm{8}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:........ \\ $$$$\:\:\:\:\:\:\:{b}=−\mathrm{4},{a}=\mathrm{1} \\ $$$${G}\left({x}\right)=\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\therefore\:\:{G}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6} \\ $$$${Verification}: \\ $$$$\begin{pmatrix}{\left.−\mathrm{1}\right)}&{\mathrm{1}}&{−\mathrm{2}}&{−\mathrm{5}}&{\mathrm{6}}\\{}&{}&{−\mathrm{1}}&{\:\:\:\mathrm{3}}&{\mathrm{2}}\\{}&{\mathrm{1}}&{−\mathrm{3}}&{\:−\mathrm{2}}&{\mathrm{8}}\end{pmatrix}\: \\ $$$$\:^{\bullet} \therefore\:\:{G}\left(−\mathrm{1}\right)=\mathrm{8} \\ $$$$\begin{pmatrix}{\left.−\mathrm{3}\right)}&{\mathrm{1}}&{−\mathrm{2}}&{−\mathrm{5}}&{\:\:\:\mathrm{6}}\\{}&{}&{−\mathrm{3}}&{\:\:\:\mathrm{15}}&{−\mathrm{30}}\\{}&{\mathrm{1}}&{−\mathrm{5}}&{\:\:\:\mathrm{10}}&{−\mathrm{24}}\end{pmatrix}\: \\ $$$$\:^{\bullet} \therefore{G}\left(−\mathrm{3}\right)=−\mathrm{24} \\ $$$$\:^{\bullet} {G}\left(\mathrm{0}\right)=\left(\mathrm{0}\right)^{\mathrm{3}} −\mathrm{2}\left(\mathrm{0}\right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{0}\right)+\mathrm{6}=\mathrm{6} \\ $$$$\:^{\bullet} \:{G}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}=\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right) \\ $$$${All}\:{conditions}\:{satisfied}. \\ $$$$\:^{\bullet} {Also}\:{by}\:{dividing}\:{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}\:{by} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)={x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{3}\:{you}\:{can}\:{see} \\ $$$${that}\:{the}\:{remainder}\:{is}\:\mathrm{16}{x}+\mathrm{24} \\ $$$${This}\:{attests}\:\left({a}\right)\:{also}. \\ $$
Commented by mr W last updated on 27/Aug/19

$${i}\:{have}\:{doubt}\:{that}\:{the}\:{solution}\:{is} \\ $$$${unique}.\:{we}\:{know}\:{only}\:{that} \\ $$$${Q}\left(\mathrm{0}\right)=−\mathrm{6}\:{and}\:{Q}\left(−\mathrm{2}\right)=−\mathrm{8}. \\ $$$${one}\:{solution}\:{is}\:{Q}\left({x}\right)={x}−\mathrm{6}\:{which} \\ $$$${means}\:{G}\left({x}\right)=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({x}−\mathrm{6}\right)+\mathrm{16}{x}+\mathrm{24} \\ $$$${or}\:{G}\left({x}\right)=\left({x}+\mathrm{2}\right)\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)\Rightarrow\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right). \\ $$$${but}\:{why}\:{not}\:{Q}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}−\mathrm{6}\:{which} \\ $$$${means}\:{G}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}\right)? \\ $$
Commented by Rasheed.Sindhi last updated on 28/Aug/19

$${I}\:{agree}\:{with}\:{you}\:{sir}!\:{This}\:{is}\:{only} \\ $$$$'{unique}\:{cubic}\:{solution}'. \\ $$$${I}\:{wanted}\:{to}\:{solve}\:{the}\:{problem}\:{in}\:{a} \\ $$$${tricky}\:{way}\:{but}\:{I}\:{failed}.{This}\:{is}\:{a} \\ $$$${lengthy}\:{and}\:{straivhtforward}\:{way}. \\ $$$${But}\:{you}\:{know}\:{something}\:{is}\:{better}\:{than} \\ $$$${nothing}. \\ $$$${I}'{ll}\:{be}\:{pleased}\:{if}\:{some}\:{one}\:{add}\:{a}\:{more} \\ $$$${compact}\:{and}\:{tricky}\:{way}! \\ $$$$\boldsymbol{{Thanks}}\:{for}\:{your}\:{precious}\:{comment} \\ $$$$\boldsymbol{{Sir}}! \\ $$
Commented by Rasheed.Sindhi last updated on 28/Aug/19

$${Sir}\:{your}\:{approach}:{to}\:{determine}\:{Q}\left({x}\right) \\ $$$${when}\:{Q}\left(\mathrm{0}\right)=−\mathrm{6}\:\&\:{Q}\left(−\mathrm{2}\right)=−\mathrm{8}\: \\ $$$$\left({Something}\:{like}\:{functional}\:{equation}\right) \\ $$$${might}\:{be}\:\:{better}\:{but}\:{again}\:{this}\:{is}\:\:{a}\:{guessing} \\ $$$${approach},{I}\:{think}. \\ $$
Commented by mr W last updated on 28/Aug/19

$${since}\:{G}\left({x}\right)=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right){Q}\left({x}\right)+\mathrm{16}{x}+\mathrm{24}, \\ $$$${we}\:{only}\:{need}\:{to}\:{determine}\:{Q}\left({x}\right). \\ $$$$ \\ $$$${from}\:{G}\left(−\mathrm{2}\right)=\mathrm{0}\:{and}\:{G}\left(\mathrm{0}\right)=\mathrm{6}\:{we} \\ $$$${get}\:{Q}\left(−\mathrm{2}\right)=−\mathrm{8}\:{and}\:{Q}\left(\mathrm{0}\right)=−\mathrm{6}.\:{that} \\ $$$${means}\:{y}={Q}\left({x}\right)\:{must}\:{pass}\:{through} \\ $$$$\left(\mathrm{0},−\mathrm{6}\right)\:{and}\:\left(−\mathrm{2},−\mathrm{8}\right).\:{but}\:{there}\:{are} \\ $$$${infinite}\:{polynomial}\:{functions}\:{which} \\ $$$${satisfy}\:{this}\:{condiction}, \\ $$$${as}\:{linear}\:{function}:\: \\ $$$${the}\:{only}\:{one}\:{is}\:{Q}\left({x}\right)={x}−\mathrm{6} \\ $$$${as}\:{quadratic}\:{function}:\: \\ $$$${infinite},\:{e}.{g}.\:{Q}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}−\mathrm{6} \\ $$$$...... \\ $$$${that}\:{is}\:{why}\:{i}\:{think}\:{the}\:{solution}\:{is} \\ $$$${not}\:{unique}. \\ $$
Commented by mr W last updated on 28/Aug/19

$${Rasheed}\:{sir},\:{i}\:{appreciate}\:{very}\:{much} \\ $$$${that}\:{you}\:{always}\:{try}\:{to}\:{go}\:{deeply}\:{behind} \\ $$$${the}\:{question},\:{not}\:{only}\:{just}\:{to}\:{give}\:{a} \\ $$$${solution}. \\ $$
Commented by Rasheed.Sindhi last updated on 28/Aug/19

$$\theta\alpha{nk}\mathcal{S}{s}\:\mathbb{S}\overset{\blacklozenge} {\mathbb{I}R}!\:{I}\:{always}\:{received}\:{encourage} \\ $$$${from}\:{you}! \\ $$
Commented by Rio Michael last updated on 29/Aug/19

$${thank}\:{you}\:{all} \\ $$
