Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 67430 by TawaTawa last updated on 27/Aug/19

Commented by MJS last updated on 27/Aug/19

coordinate method turn the triangle → CA is the base side length =s s=8+x ⇒ x=s−8 C= (((−(s/2))),(0) ) A= (((s/2)),(0) ) B= ((0),((((√3)s)/2)) ) D= ((((s/2)−3)),(0) ) E= (((5−(s/2))),(0) ) line BD l_1 : y=−(((√3)s)/(s−6))x+(((√3)s)/2) ⇒ tan θ_1 =−(((√3)s)/(s−6)) line BE l_2 : y=(((√3)s)/(s−10))x+(((√3)s)/2) ⇒ tan θ_2 =(((√3)s)/(s−10)) θ_2 −θ_1 =±30° arctan (((√3)s)/(s−10)) +arctan (((√3)s)/(s−6)) =±30° [tan (arctan α +arctan β)=((α+β)/(1−αβ))] −(((√3)(s^2 −8s))/(s^2 +8s−30))=±((√3)/3) ⇒ s=15 ⇒ x=7

$$\mathrm{coordinate}\:\mathrm{method} \\ $$$$\mathrm{turn}\:\mathrm{the}\:\mathrm{triangle}\:\rightarrow\:{CA}\:\mathrm{is}\:\mathrm{the}\:\mathrm{base} \\ $$$$\mathrm{side}\:\mathrm{length}\:={s} \\ $$$${s}=\mathrm{8}+{x}\:\Rightarrow\:{x}={s}−\mathrm{8} \\ $$$${C}=\begin{pmatrix}{−\frac{{s}}{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix}\:\:{A}=\begin{pmatrix}{\frac{{s}}{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}}\end{pmatrix} \\ $$$${D}=\begin{pmatrix}{\frac{{s}}{\mathrm{2}}−\mathrm{3}}\\{\mathrm{0}}\end{pmatrix}\:\:{E}=\begin{pmatrix}{\mathrm{5}−\frac{{s}}{\mathrm{2}}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{line}\:{BD} \\ $$$${l}_{\mathrm{1}} :\:{y}=−\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{6}}{x}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\Rightarrow\:\mathrm{tan}\:\theta_{\mathrm{1}} \:=−\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{6}} \\ $$$$\mathrm{line}\:{BE} \\ $$$${l}_{\mathrm{2}} :\:{y}=\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{10}}{x}+\frac{\sqrt{\mathrm{3}}{s}}{\mathrm{2}}\:\Rightarrow\:\mathrm{tan}\:\theta_{\mathrm{2}} \:=\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{10}} \\ $$$$\theta_{\mathrm{2}} −\theta_{\mathrm{1}} =\pm\mathrm{30}° \\ $$$$\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{10}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{s}}{{s}−\mathrm{6}}\:=\pm\mathrm{30}° \\ $$$$\:\:\:\:\:\left[\mathrm{tan}\:\left(\mathrm{arctan}\:\alpha\:+\mathrm{arctan}\:\beta\right)=\frac{\alpha+\beta}{\mathrm{1}−\alpha\beta}\right] \\ $$$$−\frac{\sqrt{\mathrm{3}}\left({s}^{\mathrm{2}} −\mathrm{8}{s}\right)}{{s}^{\mathrm{2}} +\mathrm{8}{s}−\mathrm{30}}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow\:{s}=\mathrm{15} \\ $$$$\Rightarrow\:{x}=\mathrm{7} \\ $$

Commented by TawaTawa last updated on 27/Aug/19

God bless you sir. I appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by Kunal12588 last updated on 27/Aug/19

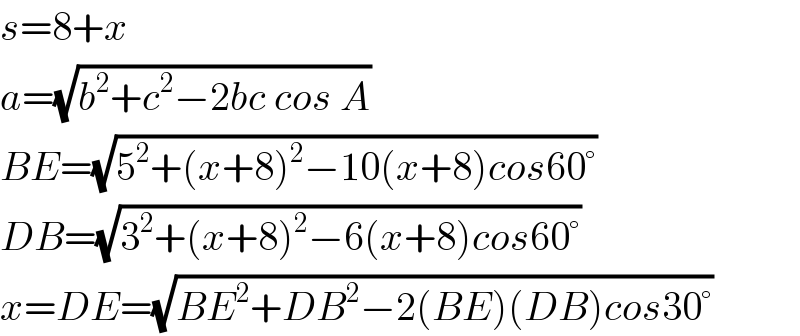
s=8+x a=(√(b^2 +c^2 −2bc cos A)) BE=(√(5^2 +(x+8)^2 −10(x+8)cos60°)) DB=(√(3^2 +(x+8)^2 −6(x+8)cos60°)) x=DE=(√(BE^2 +DB^2 −2(BE)(DB)cos30°))

$${s}=\mathrm{8}+{x} \\ $$$${a}=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:{cos}\:{A}} \\ $$$${BE}=\sqrt{\mathrm{5}^{\mathrm{2}} +\left({x}+\mathrm{8}\right)^{\mathrm{2}} −\mathrm{10}\left({x}+\mathrm{8}\right){cos}\mathrm{60}°} \\ $$$${DB}=\sqrt{\mathrm{3}^{\mathrm{2}} +\left({x}+\mathrm{8}\right)^{\mathrm{2}} −\mathrm{6}\left({x}+\mathrm{8}\right){cos}\mathrm{60}°} \\ $$$${x}={DE}=\sqrt{{BE}^{\mathrm{2}} +{DB}^{\mathrm{2}} −\mathrm{2}\left({BE}\right)\left({DB}\right){cos}\mathrm{30}°} \\ $$

Commented by TawaTawa last updated on 27/Aug/19

God bless you sir. I appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by mr W last updated on 27/Aug/19

let ∠ABD=α, ∠CBE=β α+β+30°=60° ⇒α+β=30° side length of equilateral=3+x+5=8+x ((sin α)/(AD))=((sin (α+60°))/(AB)) ((sin α)/3)=((sin (α+60°))/(8+x))=((sin α+(√3) cos α)/(2(8+x))) ((2(8+x))/3)=1+(√3) cot α ⇒cot α=((13+2x)/(3(√3)))⇒tan α=((3(√3))/(2x+13)) ((sin β)/(EC))=((sin (β+60°))/(BC)) ((sin β)/5)=((sin (β+60°))/(8+x))=((sin β+(√3) cos β)/(2(8+x))) ((2(8+x))/5)=1+(√3) cot β ⇒cot β=((11+2x)/(5(√3)))⇒tan β=((5(√3))/(2x+11)) tan (α+β)=((tan α+tan β)/(1−tan α tan β))=tan 30°=(1/(√3)) ⇒((((3(√3))/(2x+13))+((5(√3))/(2x+11)))/(1−((3(√3))/(2x+13))×((5(√3))/(2x+11))))=(1/(√3)) ⇒((3(2x+11)+5(2x+13))/((2x+13)(2x+11)−45))=(1/3) ⇒((16x+98)/(4x^2 +48x+98))=(1/3) ⇒x^2 −49=0 ⇒x=7

$${let}\:\angle{ABD}=\alpha,\:\angle{CBE}=\beta \\ $$$$\alpha+\beta+\mathrm{30}°=\mathrm{60}° \\ $$$$\Rightarrow\alpha+\beta=\mathrm{30}° \\ $$$${side}\:{length}\:{of}\:{equilateral}=\mathrm{3}+{x}+\mathrm{5}=\mathrm{8}+{x} \\ $$$$\frac{\mathrm{sin}\:\alpha}{{AD}}=\frac{\mathrm{sin}\:\left(\alpha+\mathrm{60}°\right)}{{AB}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{3}}=\frac{\mathrm{sin}\:\left(\alpha+\mathrm{60}°\right)}{\mathrm{8}+{x}}=\frac{\mathrm{sin}\:\alpha+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\alpha}{\mathrm{2}\left(\mathrm{8}+{x}\right)} \\ $$$$\frac{\mathrm{2}\left(\mathrm{8}+{x}\right)}{\mathrm{3}}=\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\alpha \\ $$$$\Rightarrow\mathrm{cot}\:\alpha=\frac{\mathrm{13}+\mathrm{2}{x}}{\mathrm{3}\sqrt{\mathrm{3}}}\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{13}} \\ $$$$\frac{\mathrm{sin}\:\beta}{{EC}}=\frac{\mathrm{sin}\:\left(\beta+\mathrm{60}°\right)}{{BC}} \\ $$$$\frac{\mathrm{sin}\:\beta}{\mathrm{5}}=\frac{\mathrm{sin}\:\left(\beta+\mathrm{60}°\right)}{\mathrm{8}+{x}}=\frac{\mathrm{sin}\:\beta+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\beta}{\mathrm{2}\left(\mathrm{8}+{x}\right)} \\ $$$$\frac{\mathrm{2}\left(\mathrm{8}+{x}\right)}{\mathrm{5}}=\mathrm{1}+\sqrt{\mathrm{3}}\:\mathrm{cot}\:\beta \\ $$$$\Rightarrow\mathrm{cot}\:\beta=\frac{\mathrm{11}+\mathrm{2}{x}}{\mathrm{5}\sqrt{\mathrm{3}}}\Rightarrow\mathrm{tan}\:\beta=\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{11}} \\ $$$$\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}=\mathrm{tan}\:\mathrm{30}°=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\frac{\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{13}}+\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{11}}}{\mathrm{1}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{13}}×\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}{x}+\mathrm{11}}}=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\frac{\mathrm{3}\left(\mathrm{2}{x}+\mathrm{11}\right)+\mathrm{5}\left(\mathrm{2}{x}+\mathrm{13}\right)}{\left(\mathrm{2}{x}+\mathrm{13}\right)\left(\mathrm{2}{x}+\mathrm{11}\right)−\mathrm{45}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{16}{x}+\mathrm{98}}{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{48}{x}+\mathrm{98}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{49}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{7} \\ $$

Commented by TawaTawa last updated on 27/Aug/19

God bless you sir. I appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by TawaTawa last updated on 27/Aug/19

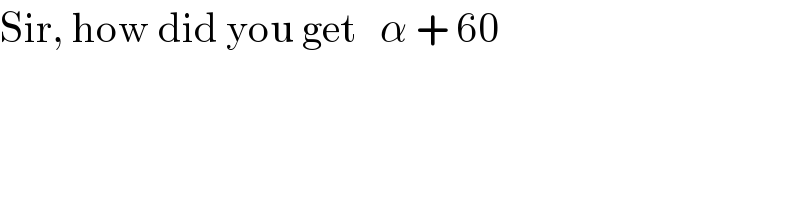
Sir, how did you get α + 60

$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\:\:\alpha\:+\:\mathrm{60} \\ $$

Commented by mr W last updated on 27/Aug/19

sin ∠ADB=sin (180°−α−∠A) =sin (α+∠A)=sin (α+60°)

$$\mathrm{sin}\:\angle{ADB}=\mathrm{sin}\:\left(\mathrm{180}°−\alpha−\angle{A}\right) \\ $$$$=\mathrm{sin}\:\left(\alpha+\angle{A}\right)=\mathrm{sin}\:\left(\alpha+\mathrm{60}°\right) \\ $$

Commented by TawaTawa last updated on 27/Aug/19

I appreciate your time sir.

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com