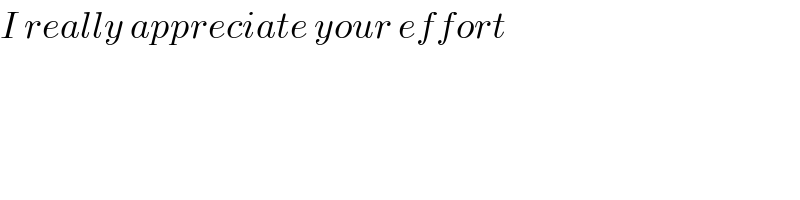Question Number 6750 by Tawakalitu. last updated on 22/Jul/16
Answered by Yozzii last updated on 22/Jul/16
$${Let}\:\angle{QPR}=\angle{RPS}=\alpha>\mathrm{0},\:\angle{PQR}=\beta>\mathrm{0}\:{and}\:\angle{PSR}=\delta>\mathrm{0}. \\ $$$${By}\:{the}\:{sine}\:{rule},\:{in}\:\bigtriangleup{QPR},\: \\ $$$$\frac{{QR}}{{sin}\alpha}=\frac{{QP}}{{sin}\angle{PRQ}}=\frac{\mathrm{3}{a}}{{sin}\left(\pi−\left(\alpha+\beta\right)\right)} \\ $$$$\Rightarrow{QR}=\frac{\mathrm{3}{asin}\alpha}{{sin}\left(\alpha+\beta\right)}. \\ $$$${In}\:\bigtriangleup{PRS},\:{by}\:{the}\:{sine}\:{rule}\:{we}\:{have} \\ $$$$\frac{{RS}}{{sin}\alpha}=\frac{{PS}}{{sin}\angle{PRS}}=\frac{{a}}{{sin}\left(\pi−\left(\alpha+\delta\right)\right)} \\ $$$${RS}=\frac{{asin}\alpha}{{sin}\left(\alpha+\delta\right)}. \\ $$$$\therefore\frac{{QR}}{{RS}}=\frac{\mathrm{3}{asin}\alpha/{sin}\left(\alpha+\beta\right)}{{asin}\alpha/{sin}\left(\alpha+\delta\right)} \\ $$$$\frac{{QR}}{{RS}}=\frac{\mathrm{3}{sin}\left(\alpha+\delta\right)}{{sin}\left(\alpha+\beta\right)} \\ $$$${Now},\:{in}\:\bigtriangleup{QPS},\:\angle{QPR}+\angle{RPS}+\angle{PSR}+\angle{RQP}=\pi. \\ $$$$\therefore\:\alpha+\alpha+\beta+\delta=\pi\Rightarrow\alpha+\delta=\pi−\left(\alpha+\beta\right). \\ $$$$\Rightarrow\frac{{QR}}{{RS}}=\frac{\mathrm{3}{sin}\left(\pi−\left(\alpha+\beta\right)\right)}{{sin}\left(\alpha+\beta\right)} \\ $$$$\frac{{QR}}{{RS}}=\frac{\mathrm{3}{sin}\left(\alpha+\beta\right)}{{sin}\left(\alpha+\beta\right)}=\frac{\mathrm{3}}{\mathrm{1}} \\ $$$$\Rightarrow{QR}:{RS}=\mathrm{3}:\mathrm{1}\Rightarrow{SR}:\left({QR}+{RS}\right)={SR}:{SQ}=\mathrm{1}:\left(\mathrm{3}+\mathrm{1}\right)=\mathrm{1}:\mathrm{4} \\ $$$${The}\:{point}\:{R}\:{divides}\:{SQ}\:{into}\:{two}\:{lengths}\:{such}\:{that} \\ $$$${the}\:{length}\:{QR}\:{is}\:\mathrm{3}\:{times}\:{the}\:{length}\:{RS}, \\ $$$${which}\:{implies}\:{that}\:{RS}\:{is}\:{one}\:{quarter} \\ $$$${the}\:{entire}\:{side}\:{SQ}\:{of}\:\bigtriangleup{QPS}. \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 22/Jul/16
$${Thanks}\:{so}\:{much}..\:{i}\:{appreciate} \\ $$
Answered by sandy_suhendra last updated on 22/Jul/16
![Let ∠QPR=∠RPS=α ∠QRP=β so ∠SRP=(180−β) In △QPR ⇒((QR)/(sin α)) = ((PQ)/(sin β)) [sin rule] ((QR)/(sinα)) = ((3a)/(sin β)) QR = ((3a sin α)/(sin β)) In △PRS ⇒ ((RS)/(sin α)) = ((PS)/(sin (180−β))) ⇒ sin (180−β)=sin β ((RS)/(sin α)) = (a/(sin β)) RS = ((a sin α)/(sin β)) ∴ QR : RS = ((3a sin α)/(sin β)) : ((a sin α)/(sin β)) = 3 :1 SR : SQ = 1 : (1+3) = 1 : 4 (I hope this answer is more simple)](Q6753.png)
$${Let}\:\angle{QPR}=\angle{RPS}=\alpha \\ $$$$\:\:\:\:\:\:\:\:\:\angle{QRP}=\beta\:{so}\:\angle{SRP}=\left(\mathrm{180}−\beta\right) \\ $$$${In}\:\bigtriangleup{QPR}\:\Rightarrow\frac{{QR}}{{sin}\:\alpha}\:=\:\frac{{PQ}}{{sin}\:\beta}\:\:\:\:\:\left[{sin}\:{rule}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{QR}}{{sin}\alpha}\:=\:\frac{\mathrm{3}{a}}{{sin}\:\beta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{QR}\:=\:\frac{\mathrm{3}{a}\:{sin}\:\alpha}{{sin}\:\beta} \\ $$$${In}\:\bigtriangleup{PRS}\:\Rightarrow\:\frac{{RS}}{{sin}\:\alpha}\:=\:\frac{{PS}}{{sin}\:\left(\mathrm{180}−\beta\right)}\:\:\:\Rightarrow\:{sin}\:\left(\mathrm{180}−\beta\right)={sin}\:\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{RS}}{{sin}\:\alpha}\:=\:\frac{{a}}{{sin}\:\beta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{RS}\:=\:\frac{{a}\:{sin}\:\alpha}{{sin}\:\beta} \\ $$$$\therefore\:\:\:\:{QR}\::\:{RS}\:=\:\frac{\mathrm{3}{a}\:{sin}\:\alpha}{{sin}\:\beta}\:\::\:\:\frac{{a}\:{sin}\:\alpha}{{sin}\:\beta}\:=\:\mathrm{3}\::\mathrm{1} \\ $$$${SR}\::\:{SQ}\:=\:\mathrm{1}\::\:\left(\mathrm{1}+\mathrm{3}\right)\:=\:\mathrm{1}\::\:\mathrm{4} \\ $$$$\left({I}\:{hope}\:{this}\:{answer}\:{is}\:{more}\:{simple}\right) \\ $$
Commented by Tawakalitu. last updated on 23/Jul/16
$${Wow}\:{thanks} \\ $$
Answered by Rasheed Soomro last updated on 22/Jul/16
Commented by Rasheed Soomro last updated on 23/Jul/16
![Answer using only geometry i-e without using trigonomeric ratios. Part-I Proving PQ : PS = QR : RS Given: _(−) △PQS, ∠1=∠2 Construction: _(−) Draw ST parallel to PR.Let ST meets produced QP at T. Proof:_(−) ∠3=∠1 [Corresponding angles] But ∠1=∠2 [Given] ∴ ∠3=∠2 [Transitive property of equality] But ∠2=∠4 [Alternative angles] ∴ ∠3=∠4 [Transitive property of equality] ∴ PS=PT [Opposite sides of equal angles] Now in △QTS ∵ PR ∥ TS [Construction] ∴ QP : PT = QR : RS [A theorm] But since PT=PS [Proved already] ∴ QP : PS = QR : RS Part-II ((QP)/(PS))=((QR)/(RS)) [Proved] ((QP)/(PS))+1=((QR)/(RS))+1 [Adding 1 to both sides] Or ((QP+PS)/(PS))=((QR+RS)/(RS)) ((QP+PS)/(PS))=((QS)/(RS)) [QR+RS=QS] Now QP=3a and PS=a [Given] ((3a+a)/a)=((QS)/(RS)) Or ((QS)/(RS)) =(4/1) RS : QS=1:4](Q6755.png)
$${Answer}\:{using}\:{only}\:{geometry}\: \\ $$$${i}-{e}\:{without}\:\:{using}\:{trigonomeric}\:{ratios}. \\ $$$$ \\ $$$${Part}-{I}\:\:{Proving}\:\:{PQ}\::\:{PS}\:=\:{QR}\::\:{RS} \\ $$$$\underset{−} {{Given}:\:\:\:\:} \\ $$$$\bigtriangleup{PQS},\:\angle\mathrm{1}=\angle\mathrm{2} \\ $$$$\underset{−} {{Construction}:\:\:\:} \\ $$$${Draw}\:{ST}\:\:{parallel}\:{to}\:{PR}.{Let}\:{ST}\:{meets}\:{produced} \\ $$$${QP}\:\:{at}\:{T}. \\ $$$$\underset{−} {{Proof}:} \\ $$$$\angle\mathrm{3}=\angle\mathrm{1}\:\:\:\:\left[{Corresponding}\:{angles}\right] \\ $$$${But}\:\angle\mathrm{1}=\angle\mathrm{2}\:\:\left[{Given}\right] \\ $$$$\therefore\:\:\:\:\angle\mathrm{3}=\angle\mathrm{2}\:\:\:\:\left[{Transitive}\:{property}\:{of}\:{equality}\right] \\ $$$${But}\:\angle\mathrm{2}=\angle\mathrm{4}\:\:\:\left[{Alternative}\:{angles}\right] \\ $$$$\therefore\:\:\:\:\:\angle\mathrm{3}=\angle\mathrm{4}\:\:\:\:\left[{Transitive}\:{property}\:{of}\:{equality}\right] \\ $$$$\therefore\:\:\:\:{PS}={PT}\:\:\:\:\left[{Opposite}\:{sides}\:{of}\:{equal}\:{angles}\right] \\ $$$${Now}\:{in}\:\bigtriangleup{QTS}\:\: \\ $$$$\:\:\:\because\:{PR}\:\parallel\:{TS}\:\:\left[{Construction}\right] \\ $$$$\therefore\:\:{QP}\::\:{PT}\:=\:{QR}\::\:{RS}\:\:\:\left[{A}\:{theorm}\right] \\ $$$${But}\:{since}\:{PT}={PS}\:\:\left[{Proved}\:{already}\right] \\ $$$$\therefore\:\:\:{QP}\::\:{PS}\:=\:{QR}\::\:{RS} \\ $$$$ \\ $$$${Part}-{II} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{QP}}{{PS}}=\frac{{QR}}{{RS}}\:\:\:\left[{Proved}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{QP}}{{PS}}+\mathrm{1}=\frac{{QR}}{{RS}}+\mathrm{1}\:\:\left[{Adding}\:\mathrm{1}\:{to}\:{both}\:{sides}\right] \\ $$$$\:{Or}\:\:\:\:\:\:\:\:\frac{{QP}+{PS}}{{PS}}=\frac{{QR}+{RS}}{{RS}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{QP}+{PS}}{{PS}}=\frac{{QS}}{{RS}}\:\:\:\:\left[{QR}+{RS}={QS}\right] \\ $$$${Now}\:{QP}=\mathrm{3}{a}\:\:{and}\:\:\:\:{PS}={a}\:\:\:\:\left[{Given}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}{a}+{a}}{{a}}=\frac{{QS}}{{RS}}\:\: \\ $$$${Or}\:\:\:\:\frac{{QS}}{{RS}}\:\:=\frac{\mathrm{4}}{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:{RS}\::\:{QS}=\mathrm{1}:\mathrm{4} \\ $$
Commented by Tawakalitu. last updated on 23/Jul/16
$${I}\:{really}\:{appreciate}\:{your}\:{effort} \\ $$