
Previous in Relation and Functions Next in Relation and Functions
Question Number 67532 by mathmax by abdo last updated on 28/Aug/19

$${prove}\:{that}\:\:\pi\:{cotan}\left(\pi\alpha\right)\:={lim}_{{n}\rightarrow+\infty} \:\:\:\sum_{{k}=−{n}} ^{{n}} \:\:\frac{\mathrm{1}}{\alpha−{k}} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19
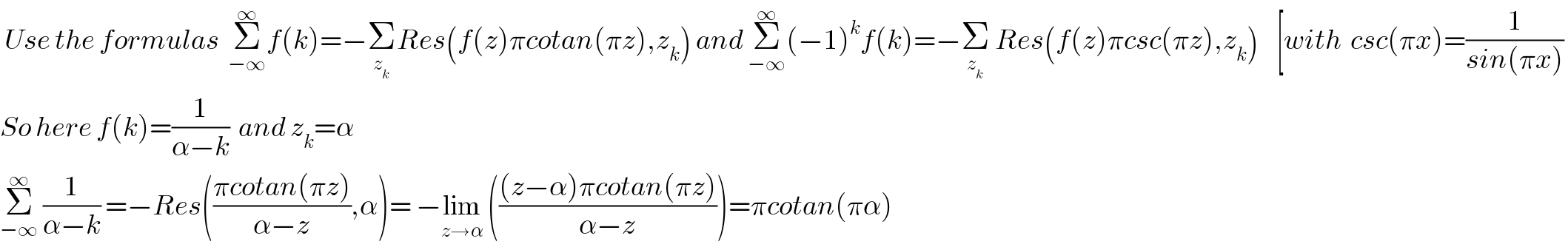
$$\:{Use}\:{the}\:{formulas}\:\:\underset{−\infty} {\overset{\infty} {\sum}}{f}\left({k}\right)=−\underset{{z}_{{k}} } {\sum}{Res}\left({f}\left({z}\right)\pi{cotan}\left(\pi{z}\right),{z}_{{k}} \right)\:{and}\:\underset{−\infty} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {f}\left({k}\right)=−\underset{{z}_{{k}} } {\sum}\:{Res}\left({f}\left({z}\right)\pi{csc}\left(\pi{z}\right),{z}_{{k}} \right)\:\:\:\:\left[{with}\:\:{csc}\left(\pi{x}\right)=\frac{\mathrm{1}}{{sin}\left(\pi{x}\right)}\:\right. \\ $$$${So}\:{here}\:{f}\left({k}\right)=\frac{\mathrm{1}}{\alpha−{k}}\:\:{and}\:{z}_{{k}} =\alpha \\ $$$$\underset{−\infty} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\alpha−{k}}\:=−{Res}\left(\frac{\pi{cotan}\left(\pi{z}\right)}{\alpha−{z}},\alpha\right)=\:−\underset{{z}\rightarrow\alpha} {\mathrm{lim}}\:\left(\frac{\left({z}−\alpha\right)\pi{cotan}\left(\pi{z}\right)}{\alpha−{z}}\right)=\pi{cotan}\left(\pi\alpha\right) \\ $$
