
Previous in Relation and Functions Next in Relation and Functions
Question Number 67537 by mathmax by abdo last updated on 28/Aug/19
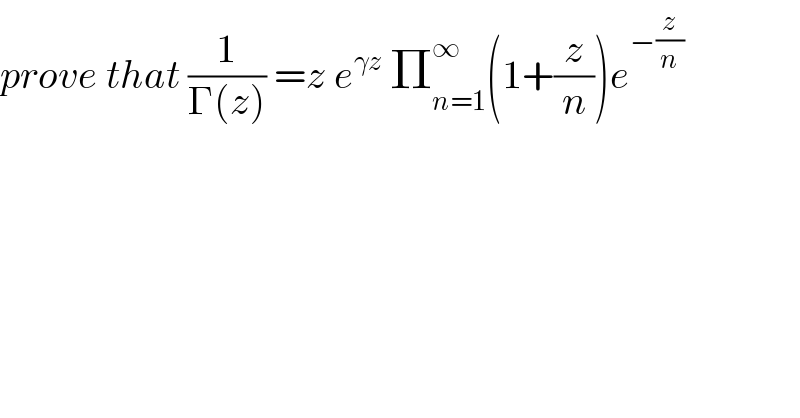
$${prove}\:{that}\:\frac{\mathrm{1}}{\Gamma\left({z}\right)}\:={z}\:{e}^{\gamma{z}} \:\prod_{{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}+\frac{{z}}{{n}}\right){e}^{−\frac{{z}}{{n}}} \\ $$
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19
![Let use the result (1/(Γ(z)))=lim_(n→∞ ) ((z(z+1)...(z+n))/(n^z n!)) (1/(Γ(z)))=lim_(n→∞) ze^(−zln(n)) ((Π_(k=1) ^n (z+k))/(Π_(k=1) ^n k)) =lim_(n→∞) ze^(−zln(n)) Π_(k=1) ^n [(1+(z/k))e^((−z)/k) .e^(z/k) ] =lim_(n→∞) zΠ_(k=1) ^n [(1+(z/k))e^(−(z/k)) ] e^(z(−ln(n)+Σ_(k=1) ^n (1/k) )) =zΠ_(k=1) ^∞ [(1+(z/k))e^(−(z/k)) ]e^(zγ) cause lim_(n→∞) Σ_(k=1) ^∞ (1/k) −ln(n)=γ](Q67587.png)
$$ \\ $$$$ \\ $$$${Let}\:{use}\:{the}\:{result}\:\frac{\mathrm{1}}{\Gamma\left({z}\right)}=\underset{{n}\rightarrow\infty\:} {\mathrm{lim}}\:\frac{{z}\left({z}+\mathrm{1}\right)...\left({z}+{n}\right)}{{n}^{{z}} \:{n}!}\: \\ $$$$\frac{\mathrm{1}}{\Gamma\left({z}\right)}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{ze}^{−{zln}\left({n}\right)} \:\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left({z}+{k}\right)}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{k}}\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{ze}^{−{zln}\left({n}\right)} \underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left[\left(\mathrm{1}+\frac{{z}}{{k}}\right){e}^{\frac{−{z}}{{k}}} .{e}^{\frac{{z}}{{k}}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{z}\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left[\left(\mathrm{1}+\frac{{z}}{{k}}\right){e}^{−\frac{{z}}{{k}}} \right]\:{e}^{{z}\left(−{ln}\left({n}\right)+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}\:\right)} \\ $$$$\:\:={z}\underset{{k}=\mathrm{1}} {\overset{\infty} {\prod}}\left[\left(\mathrm{1}+\frac{{z}}{{k}}\right){e}^{−\frac{{z}}{{k}}} \right]{e}^{{z}\gamma} \:\:\:\:\:\:\:\:{cause}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}\:−{ln}\left({n}\right)=\gamma \\ $$$$ \\ $$$$ \\ $$
