
Previous in Relation and Functions Next in Relation and Functions
Question Number 67538 by mathmax by abdo last updated on 28/Aug/19
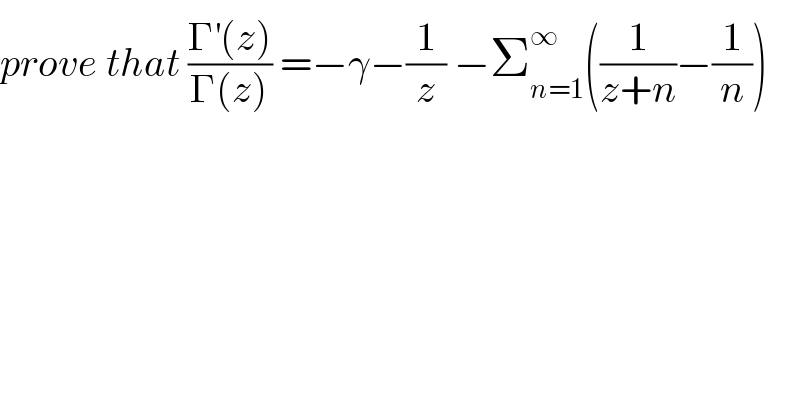
$${prove}\:{that}\:\frac{\Gamma^{'} \left({z}\right)}{\Gamma\left({z}\right)}\:=−\gamma−\frac{\mathrm{1}}{{z}}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{z}+{n}}−\frac{\mathrm{1}}{{n}}\right) \\ $$
Commented by ~ À ® @ 237 ~ last updated on 29/Aug/19
![It is known that Γ(z+n)=z(z+1)(z+2).....(z+n−1)Γ(z) So lnΓ(z+n)=lnΓ(z) +Σ_(k=0) ^(n−1) ln(z+k) Now we have lnΓ(z)=lnΓ(z+n)−lnz−Σ_(k=1) ^(n−1) [ln(z+k)−(z/k)−lnk] −Σ_(k=1) ^(n−1) (z/k) −Σ_(k=1) ^(n−1) lnk −zln(n)+zln(n) =lnΓ(z+n)−lnΓ(n)−zln(n)−lnz−Σ_(k=1) ^(n−1) [ln(z+k)−(z/k)−lnk]+z[ln(n)−Σ_(k=1) ^(n−1) (1/k)] cause Σ_(k=1) ^(n−1) lnk=ln((n−1)!)=lnΓ(n) =ln[((Γ(z+n))/(n^z Γ(n)))]−lnz−Σ_(k=1) ^(n−1) [ln(z+k)−(z/k)−lnk]+z(ln(n)−H_(n−1) ) (•) Now let find L=lim_(n→∞) ((Γ(z+n))/(n^z Γ(n))) L=lim_(n→∞) ((z(z+1)...(z+n))/(n^z n!)) ((nΓ(z))/(z+n)) = 1 cause lim_(n→∞ ) ((z(z+1)...(z+n))/(n^z n!)) =(1/(Γ(z))) So we have lim_(n→∞) lnΓ(z)=ln1−lnz−Σ_(k=1_ ) ^∞ [ln(z+k)−(z/k)−lnk]−zγ cquse lim_(n→∞) (ln(n) −H_(n−1) )=−γ lnΓ(z)=−zγ−lnz−Σ_(k=1 ) ^∞ [ln(z+k)−(z/k)−lnk] Finally when derivating on z we get ((Γ′(z))/(Γ(z)))=−γ−(1/z)−Σ_(k=1) ^∞ ((1/(z+k))−(1/k))](Q67585.png)
$$ \\ $$$$ \\ $$$${It}\:{is}\:{known}\:{that}\:\Gamma\left({z}+{n}\right)={z}\left({z}+\mathrm{1}\right)\left({z}+\mathrm{2}\right).....\left({z}+{n}−\mathrm{1}\right)\Gamma\left({z}\right) \\ $$$${So}\:\:{ln}\Gamma\left({z}+{n}\right)={ln}\Gamma\left({z}\right)\:+\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{ln}\left({z}+{k}\right)\: \\ $$$${Now}\:{we}\:{have} \\ $$$${ln}\Gamma\left({z}\right)={ln}\Gamma\left({z}+{n}\right)−{lnz}−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[{ln}\left({z}+{k}\right)−\frac{{z}}{{k}}−{lnk}\right]\:\:−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{z}}{{k}}\:−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{lnk}\:\:−{zln}\left({n}\right)+{zln}\left({n}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:={ln}\Gamma\left({z}+{n}\right)−{ln}\Gamma\left({n}\right)−{zln}\left({n}\right)−{lnz}−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[{ln}\left({z}+{k}\right)−\frac{{z}}{{k}}−{lnk}\right]+{z}\left[{ln}\left({n}\right)−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{k}}\right]\:\:\:\:\:{cause}\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{lnk}={ln}\left(\left({n}−\mathrm{1}\right)!\right)={ln}\Gamma\left({n}\right) \\ $$$$\:\:\:\:\:\:\:\:\:={ln}\left[\frac{\Gamma\left({z}+{n}\right)}{{n}^{{z}} \Gamma\left({n}\right)}\right]−{lnz}−\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[{ln}\left({z}+{k}\right)−\frac{{z}}{{k}}−{lnk}\right]+{z}\left({ln}\left({n}\right)−{H}_{{n}−\mathrm{1}} \right)\:\:\:\:\:\:\left(\bullet\right) \\ $$$${Now}\:{let}\:{find}\:{L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\Gamma\left({z}+{n}\right)}{{n}^{{z}} \Gamma\left({n}\right)}\: \\ $$$${L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{{z}\left({z}+\mathrm{1}\right)...\left({z}+{n}\right)}{{n}^{{z}} \:{n}!}\:\frac{{n}\Gamma\left({z}\right)}{{z}+{n}}\:=\:\mathrm{1}\:\:\:{cause}\:\:\underset{{n}\rightarrow\infty\:} {\mathrm{lim}}\:\frac{{z}\left({z}+\mathrm{1}\right)...\left({z}+{n}\right)}{{n}^{{z}} \:{n}!}\:=\frac{\mathrm{1}}{\Gamma\left({z}\right)}\: \\ $$$${So}\:\:{we}\:{have} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{ln}\Gamma\left({z}\right)={ln}\mathrm{1}−{lnz}−\underset{{k}=\mathrm{1}_{} } {\overset{\infty} {\sum}}\left[{ln}\left({z}+{k}\right)−\frac{{z}}{{k}}−{lnk}\right]−{z}\gamma\:\:\:\:\:\:\:\:\:{cquse}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left({ln}\left({n}\right)\:−{H}_{{n}−\mathrm{1}} \right)=−\gamma \\ $$$${ln}\Gamma\left({z}\right)=−{z}\gamma−{lnz}−\underset{{k}=\mathrm{1}\:} {\overset{\infty} {\sum}}\left[{ln}\left({z}+{k}\right)−\frac{{z}}{{k}}−{lnk}\right] \\ $$$${Finally}\:\:{when}\:{derivating}\:\:{on}\:{z}\:{we}\:{get} \\ $$$$\frac{\Gamma'\left({z}\right)}{\Gamma\left({z}\right)}=−\gamma−\frac{\mathrm{1}}{{z}}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{z}+{k}}−\frac{\mathrm{1}}{{k}}\right) \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 29/Aug/19

$${thank}\:{you}\:{sir}. \\ $$
