
Question Number 67539 by mathmax by abdo last updated on 28/Aug/19
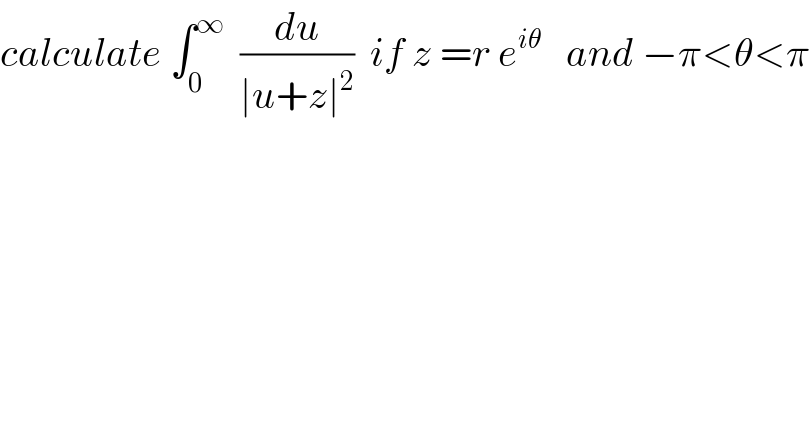
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mid{u}+{z}\mid^{\mathrm{2}} }\:\:{if}\:{z}\:={r}\:{e}^{{i}\theta} \:\:\:{and}\:−\pi<\theta<\pi \\ $$
Commented by~ À ® @ 237 ~ last updated on 29/Aug/19
![∣u+z∣^2 =(u+z)(u+z^_ ) I=(1/(z−z^_ )) ∫_0 ^∞ ((1/(u+z^_ )) −(1/(u+z ))) du =(1/(2iIm(z)))[ln(((u+z^_ )/(u+z)))]_0 ^∞ =(1/(2irsinθ)) [ln1−ln(e^(−i2θ) )]=(θ/(rsinθ))](Q67588.png)
$$\mid{u}+{z}\mid^{\mathrm{2}} =\left({u}+{z}\right)\left({u}+\overset{\_} {{z}}\right)\: \\ $$ $${I}=\frac{\mathrm{1}}{{z}−\overset{\_} {{z}}}\:\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{u}+\overset{\_} {{z}}}\:−\frac{\mathrm{1}}{{u}+{z}\:}\right)\:{du}\:=\frac{\mathrm{1}}{\mathrm{2}{iIm}\left({z}\right)}\left[{ln}\left(\frac{{u}+\overset{\_} {{z}}}{{u}+{z}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{2}{irsin}\theta}\:\left[{ln}\mathrm{1}−{ln}\left({e}^{−{i}\mathrm{2}\theta} \:\right)\right]=\frac{\theta}{{rsin}\theta} \\ $$ $$ \\ $$
Commented bymathmax by abdo last updated on 29/Aug/19

$${thank}\:{you}\:{sir}. \\ $$
Commented bymathmax by abdo last updated on 29/Aug/19
![let I =∫_0 ^∞ (du/(∣u+z∣^2 )) ⇒ I =∫_0 ^∞ (du/((u+z)(u+z^− ))) =(1/(z−z^− ))∫_0 ^∞ ((1/(u+z^− ))−(1/(u+z)))du =(1/(2i(rsinθ))) [ln(((u+z^− )/(u+z)))]_0 ^(+∞) =(1/(2ir sinθ))×(−ln((z^− /z)) ) we have −ln((z^− /z))=ln((z/z^− )) (z/z^− ) =(z^2 /(∣z∣^2 )) =((r^2 e^(2iθ) )/r^2 ) =e^(2iθ) ⇒ln((z/z^− )) =2iθ ⇒ I =(1/(2ir sinθ))×(2iθ) ⇒I =(θ/(r sinθ)) .](Q67658.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mid{u}+{z}\mid^{\mathrm{2}} }\:\Rightarrow\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\left({u}+{z}\right)\left({u}+\overset{−} {{z}}\right)} \\ $$ $$=\frac{\mathrm{1}}{{z}−\overset{−} {{z}}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{u}+\overset{−} {{z}}}−\frac{\mathrm{1}}{{u}+{z}}\right){du}\:=\frac{\mathrm{1}}{\mathrm{2}{i}\left({rsin}\theta\right)}\:\left[{ln}\left(\frac{{u}+\overset{−} {{z}}}{{u}+{z}}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}{ir}\:{sin}\theta}×\left(−{ln}\left(\frac{\overset{−} {{z}}}{{z}}\right)\:\right)\:{we}\:{have}\:−{ln}\left(\frac{\overset{−} {{z}}}{{z}}\right)={ln}\left(\frac{{z}}{\overset{−} {{z}}}\right) \\ $$ $$\frac{{z}}{\overset{−} {{z}}}\:=\frac{{z}^{\mathrm{2}} }{\mid{z}\mid^{\mathrm{2}} }\:=\frac{{r}^{\mathrm{2}} \:{e}^{\mathrm{2}{i}\theta} }{{r}^{\mathrm{2}} }\:={e}^{\mathrm{2}{i}\theta} \:\Rightarrow{ln}\left(\frac{{z}}{\overset{−} {{z}}}\right)\:=\mathrm{2}{i}\theta\:\Rightarrow \\ $$ $${I}\:=\frac{\mathrm{1}}{\mathrm{2}{ir}\:{sin}\theta}×\left(\mathrm{2}{i}\theta\right)\:\Rightarrow{I}\:=\frac{\theta}{{r}\:{sin}\theta}\:. \\ $$
