Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 67542 by mathmax by abdo last updated on 28/Aug/19

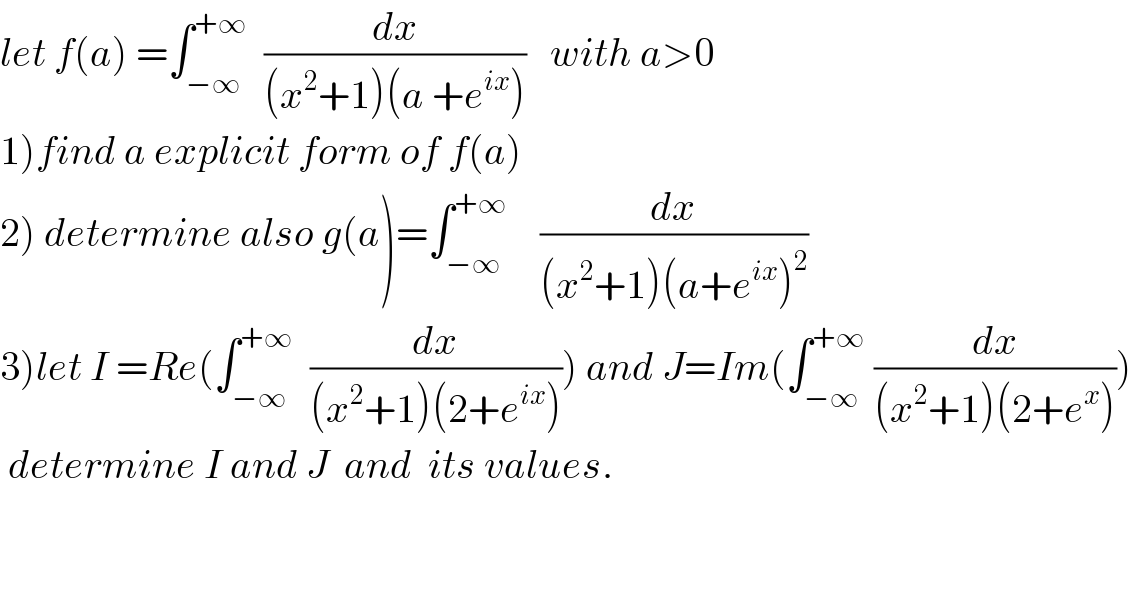
let f(a) =∫_(−∞) ^(+∞) (dx/((x^2 +1)(a +e^(ix) ))) with a>0 1)find a explicit form of f(a) 2) determine also g(a)=∫_(−∞) ^(+∞) (dx/((x^2 +1)(a+e^(ix) )^2 )) 3)let I =Re(∫_(−∞) ^(+∞) (dx/((x^2 +1)(2+e^(ix) )))) and J=Im(∫_(−∞) ^(+∞) (dx/((x^2 +1)(2+e^x )))) determine I and J and its values.

$${let}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({a}\:+{e}^{{ix}} \right)}\:\:\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{1}\right){find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({a}\right) \\ $$ $$\left.\mathrm{2}\right)\:{determine}\:{also}\:{g}\left({a}\right)=\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({a}+{e}^{{ix}} \right)^{\mathrm{2}} } \\ $$ $$\left.\mathrm{3}\right){let}\:{I}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}+{e}^{{ix}} \right)}\right)\:{and}\:{J}={Im}\left(\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}+{e}^{{x}} \right)}\right) \\ $$ $$\:{determine}\:{I}\:{and}\:{J}\:\:{and}\:\:{its}\:{values}. \\ $$

Commented by~ À ® @ 237 ~ last updated on 29/Aug/19

let change x=tanu f(a)=∫_(−(π/2)) ^(π/2) (du/(h(u))) with h(u)=a+e^(itanu) g has only one root on [((−π)/2);(π/2)] let named it θ When using the RT f(a)=2πiRes((1/h),θ) =((2iπ)/(h′(θ)))=((2iπ)/(i(1+tan^2 θ)e^(itanθ) )) θ root of h ⇒ e^(itanθ) =−a and tanθ=π−ilna So f(a)=((2π)/(−a(1+π^2 +(lna)^2 −2πilna))) we can ascertain that g(a)=(df/da) When stating x(a)=1+π^2 +(lna)^2 and y(a)=2πlna Re(f(a))=−((2π)/a) ((x(a))/(x^2 (a)+y^2 (a))) and Im(f(a))=((−2π)/a) ((y(a))/(x^2 (a)+y^2 (a)))

$${let}\:{change}\:{x}={tanu}\: \\ $$ $${f}\left({a}\right)=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{du}}{{h}\left({u}\right)}\:\:\:\:\:\:\:\:{with}\:\:\:{h}\left({u}\right)={a}+{e}^{{itanu}} \:\:\:\:\: \\ $$ $${g}\:{has}\:{only}\:{one}\:{root}\:{on}\:\left[\frac{−\pi}{\mathrm{2}};\frac{\pi}{\mathrm{2}}\right]\:{let}\:{named}\:{it}\:\:\theta \\ $$ $${When}\:{using}\:{the}\:{RT}\:\: \\ $$ $${f}\left({a}\right)=\mathrm{2}\pi{iRes}\left(\frac{\mathrm{1}}{{h}},\theta\right)\:=\frac{\mathrm{2}{i}\pi}{{h}'\left(\theta\right)}=\frac{\mathrm{2}{i}\pi}{{i}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){e}^{{itan}\theta} }\: \\ $$ $$\theta\:{root}\:{of}\:{h}\:\Rightarrow\:{e}^{{itan}\theta} =−{a}\:\:{and}\:\:{tan}\theta=\pi−{ilna} \\ $$ $${So}\:\:{f}\left({a}\right)=\frac{\mathrm{2}\pi}{−{a}\left(\mathrm{1}+\pi^{\mathrm{2}} +\left({lna}\right)^{\mathrm{2}} −\mathrm{2}\pi{ilna}\right)} \\ $$ $${we}\:{can}\:{ascertain}\:{that}\:\:{g}\left({a}\right)=\frac{{df}}{{da}}\: \\ $$ $${When}\:{stating}\:\:{x}\left({a}\right)=\mathrm{1}+\pi^{\mathrm{2}} +\left({lna}\right)^{\mathrm{2}} \:\:{and}\:\:{y}\left({a}\right)=\mathrm{2}\pi{lna}\: \\ $$ $${Re}\left({f}\left({a}\right)\right)=−\frac{\mathrm{2}\pi}{{a}}\:\frac{{x}\left({a}\right)}{{x}^{\mathrm{2}} \left({a}\right)+{y}^{\mathrm{2}} \left({a}\right)}\:\:{and}\:{Im}\left({f}\left({a}\right)\right)=\frac{−\mathrm{2}\pi}{{a}}\:\frac{{y}\left({a}\right)}{{x}^{\mathrm{2}} \left({a}\right)+{y}^{\mathrm{2}} \left({a}\right)}\: \\ $$

Commented bymathmax by abdo last updated on 29/Aug/19

thank you sir.

$${thank}\:{you}\:{sir}. \\ $$

Commented bymathmax by abdo last updated on 29/Aug/19

1)let consider tbe complex function W(z)=(1/((z^2 +1)(a +e^(iz) ))) ⇒W(z) =(1/((z−i)(z+i)(a+e^(iz) ))) the poles of W are i and −i residus theorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,i) Res(W,i) =lim_(z→i) (z−i)W(z) =(1/((2i)(a+e^(−1) ))) ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ×(1/(2i(a+e^(−1) ))) =(π/(a+e^(−1) )) =((πe)/(ae +1)) ⇒ f(a) =((πe)/(ae +1)) with a>0 2) we have f^′ (a) =−∫_(−∞) ^(+∞) (dx/((x^2 +1)(a+e^(ix) )^2 )) =−g(a) ⇒ g(a) =−f^′ (a) but f(a) =((πe)/(ae +1)) ⇒f^′ (a) =−((πe^2 )/((ae +1)^2 )) ⇒ g(a) =((πe^2 )/((ae +1)^2 )) .

$$\left.\mathrm{1}\right){let}\:{consider}\:{tbe}\:{complex}\:{function}\:{W}\left({z}\right)=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)\left({a}\:+{e}^{{iz}} \right)} \\ $$ $$\Rightarrow{W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{i}\right)\left({z}+{i}\right)\left({a}+{e}^{{iz}} \right)}\:\:{the}\:{poles}\:{of}\:{W}\:{are}\:{i}\:{and}\:−{i} \\ $$ $${residus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({W},{i}\right) \\ $$ $${Res}\left({W},{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\left({z}−{i}\right){W}\left({z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{2}{i}\right)\left({a}+{e}^{−\mathrm{1}} \right)}\:\Rightarrow \\ $$ $$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi×\frac{\mathrm{1}}{\mathrm{2}{i}\left({a}+{e}^{−\mathrm{1}} \right)}\:=\frac{\pi}{{a}+{e}^{−\mathrm{1}} }\:=\frac{\pi{e}}{{ae}\:+\mathrm{1}}\:\Rightarrow \\ $$ $${f}\left({a}\right)\:=\frac{\pi{e}}{{ae}\:+\mathrm{1}}\:\:{with}\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right)\:{we}\:{have}\:\:{f}^{'} \left({a}\right)\:=−\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({a}+{e}^{{ix}} \right)^{\mathrm{2}} }\:=−{g}\left({a}\right)\:\Rightarrow \\ $$ $${g}\left({a}\right)\:=−{f}^{'} \left({a}\right)\:\:\:{but}\:{f}\left({a}\right)\:=\frac{\pi{e}}{{ae}\:+\mathrm{1}}\:\:\Rightarrow{f}^{'} \left({a}\right)\:=−\frac{\pi{e}^{\mathrm{2}} }{\left({ae}\:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$ $${g}\left({a}\right)\:=\frac{\pi{e}^{\mathrm{2}} }{\left({ae}\:+\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$ $$ \\ $$

Commented bymathmax by abdo last updated on 29/Aug/19

3) we have f(a) =∫_(−∞) ^(+∞) (dx/((x^2 +1)(a +cosx +isinx))) =∫_(−∞) ^(+∞) ((a+cosx−isinx)/((x^2 +1)((a+cosx)^2 +sin^2 x)))dx =∫_(−∞) ^(+∞) ((a+cosx)/((x^2 +1){a^2 +2acosx +1)}))dx −i ∫_(−∞) ^(+∞) ((sinx)/((x^2 +1){ a^2 +2acosx +1}))dx ⇒ Re(f(a)) =∫_(−∞) ^(+∞) ((a+cosx)/((x^2 +1){ a^2 +2acosx +1}))dx and Im(f(a)) =∫_(−∞) ^(+∞) ((sinx dx)/((x^2 +1){a^2 +2acosx +1}))=0 because the function x →((sinx)/((x^2 +1){a^2 +2a cosx +1})) is odd.

$$\left.\mathrm{3}\right)\:{we}\:{have}\:{f}\left({a}\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({a}\:+{cosx}\:+{isinx}\right)} \\ $$ $$=\int_{−\infty} ^{+\infty} \:\:\frac{{a}+{cosx}−{isinx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\left({a}+{cosx}\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} {x}\right)}{dx} \\ $$ $$=\int_{−\infty} ^{+\infty} \:\:\frac{{a}+{cosx}}{\left.\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left\{{a}^{\mathrm{2}} \:+\mathrm{2}{acosx}\:+\mathrm{1}\right)\right\}}{dx}\:−{i}\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{{sinx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left\{\:{a}^{\mathrm{2}} \:+\mathrm{2}{acosx}\:+\mathrm{1}\right\}}{dx} \\ $$ $$\Rightarrow\:{Re}\left({f}\left({a}\right)\right)\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{a}+{cosx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left\{\:{a}^{\mathrm{2}} \:+\mathrm{2}{acosx}\:+\mathrm{1}\right\}}{dx}\:{and} \\ $$ $${Im}\left({f}\left({a}\right)\right)\:=\int_{−\infty} ^{+\infty} \:\:\frac{{sinx}\:{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left\{{a}^{\mathrm{2}} \:+\mathrm{2}{acosx}\:+\mathrm{1}\right\}}=\mathrm{0}\:{because}\:{the}\: \\ $$ $${function}\:{x}\:\rightarrow\frac{{sinx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left\{{a}^{\mathrm{2}} \:+\mathrm{2}{a}\:{cosx}\:+\mathrm{1}\right\}}\:{is}\:{odd}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com