Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 6758 by FilupSmith last updated on 23/Jul/16

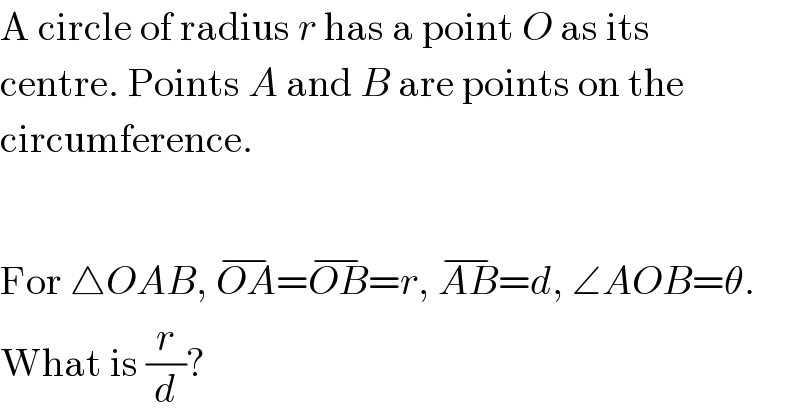
A circle of radius r has a point O as its centre. Points A and B are points on the circumference. For △OAB, OA^(−) =OB^(−) =r, AB^(−) =d, ∠AOB=θ. What is (r/d)?

$$\mathrm{A}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:{r}\:\mathrm{has}\:\mathrm{a}\:\mathrm{point}\:{O}\:\mathrm{as}\:\mathrm{its} \\ $$$$\mathrm{centre}.\:\mathrm{Points}\:{A}\:\mathrm{and}\:{B}\:\mathrm{are}\:\mathrm{points}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{circumference}. \\ $$$$ \\ $$$$\mathrm{For}\:\bigtriangleup{OAB},\:\overline {{OA}}=\overline {{OB}}={r},\:\overline {{AB}}={d},\:\angle{AOB}=\theta. \\ $$$$\mathrm{What}\:\mathrm{is}\:\frac{{r}}{{d}}? \\ $$

Commented by FilupSmith last updated on 23/Jul/16

I′ve used the cosine rule and pythagorus and have gotten two different results for the variable d.

$$\mathrm{I}'\mathrm{ve}\:\mathrm{used}\:\mathrm{the}\:\mathrm{cosine}\:\mathrm{rule}\:\mathrm{and}\:\mathrm{pythagorus} \\ $$$$\mathrm{and}\:\mathrm{have}\:\mathrm{gotten}\:\mathrm{two}\:\mathrm{different}\:\mathrm{results}\:\mathrm{for} \\ $$$$\mathrm{the}\:\mathrm{variable}\:{d}. \\ $$

Commented by Rasheed Soomro last updated on 23/Jul/16

By cosine law d^( 2) =r^2 +r^2 −2r^2 coθ=2r^2 (1−cosθ) (r^2 /d^( 2) )=(1/(2(1−cosθ))) (r/d)=+(√(1/(2(1−cosθ)))) [Since r,d>0 , (r/d)>0] =(1/(√(2(1−cosθ))))........................A −−−−−−−−− By Pythagorus theorm sin(θ/2)=((d/2)/r)=(d/(2r)) (d/r)=2sin(θ/2) But sin(θ/2)=±(√((1−cosθ)/2)) Hence (d/r)=2(+(√((1−cosθ)/2))) [Since r,d>0 , (r/d)>0] (r/d)=(1/2)(((√2)/(√(1−cosθ))))=(1/(√2))((1/(√(1−cosθ)))) =(1/(√(2(1−cosθ)))).......................B Both results are same.

$${By}\:{cosine}\:{law} \\ $$$${d}^{\:\mathrm{2}} ={r}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{r}^{\mathrm{2}} {co}\theta=\mathrm{2}{r}^{\mathrm{2}} \left(\mathrm{1}−{cos}\theta\right) \\ $$$$\frac{{r}^{\mathrm{2}} }{{d}^{\:\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{cos}\theta\right)} \\ $$$$\frac{{r}}{{d}}=+\sqrt{\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{cos}\theta\right)}}\:\:\:\left[{Since}\:\:{r},{d}>\mathrm{0}\:,\:\:\frac{{r}}{{d}}>\mathrm{0}\right] \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}\left(\mathrm{1}−{cos}\theta\right)}}........................{A} \\ $$$$−−−−−−−−− \\ $$$${By}\:{Pythagorus}\:{theorm} \\ $$$${sin}\frac{\theta}{\mathrm{2}}=\frac{{d}/\mathrm{2}}{{r}}=\frac{{d}}{\mathrm{2}{r}} \\ $$$$\frac{{d}}{{r}}=\mathrm{2}{sin}\frac{\theta}{\mathrm{2}} \\ $$$${But}\:\:{sin}\frac{\theta}{\mathrm{2}}=\pm\sqrt{\frac{\mathrm{1}−{cos}\theta}{\mathrm{2}}} \\ $$$${Hence}\:\:\:\frac{{d}}{{r}}=\mathrm{2}\left(+\sqrt{\frac{\mathrm{1}−{cos}\theta}{\mathrm{2}}}\right)\:\:\left[{Since}\:\:{r},{d}>\mathrm{0}\:,\:\:\frac{{r}}{{d}}>\mathrm{0}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{r}}{{d}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{1}−{cos}\theta}}\right)=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{cos}\theta}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}\left(\mathrm{1}−{cos}\theta\right)}}.......................{B} \\ $$$${Both}\:{results}\:{are}\:{same}. \\ $$$$ \\ $$

Commented by FilupSmith last updated on 24/Jul/16

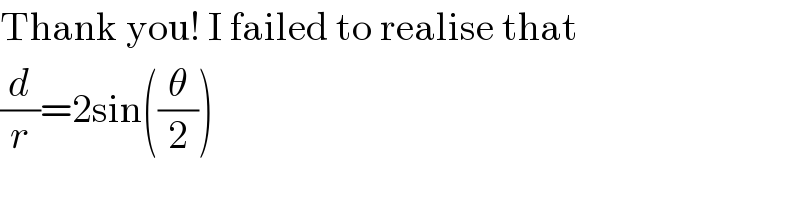
Thank you! I failed to realise that (d/r)=2sin((θ/2))

$$\mathrm{Thank}\:\mathrm{you}!\:\mathrm{I}\:\mathrm{failed}\:\mathrm{to}\:\mathrm{realise}\:\mathrm{that} \\ $$$$\frac{{d}}{{r}}=\mathrm{2sin}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$

Commented by sandy_suhendra last updated on 25/Jul/16

(r/d) = (1/(√(2 (1−cos θ)))) (d/r) = (√(2 (1−cos θ))) ⇒ 1−cos θ = 2 sin^2 ((θ/2)) (d/r) = (√(4 sin^2 ((θ/2)))) = 2 sin ((θ/2))

$$\frac{{r}}{{d}}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}\:\left(\mathrm{1}−{cos}\:\theta\right)}}\: \\ $$$$\frac{{d}}{{r}}\:=\:\sqrt{\mathrm{2}\:\left(\mathrm{1}−{cos}\:\theta\right)}\:\:\:\:\Rightarrow\:\mathrm{1}−{cos}\:\theta\:=\:\mathrm{2}\:{sin}^{\mathrm{2}} \:\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$\frac{{d}}{{r}}\:=\:\sqrt{\mathrm{4}\:{sin}^{\mathrm{2}} \:\left(\frac{\theta}{\mathrm{2}}\right)}\:\:=\:\mathrm{2}\:{sin}\:\left(\frac{\theta}{\mathrm{2}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com