Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 67673 by Abdo msup. last updated on 30/Aug/19

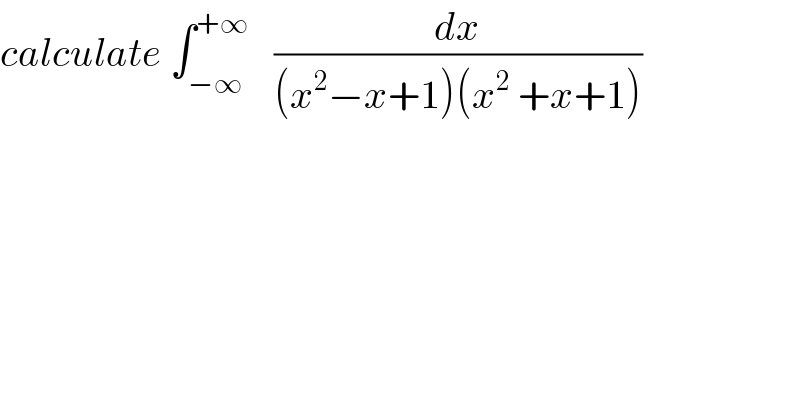
calculate ∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +x+1)))

$${calculate}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)} \\ $$

Commented by Abdo msup. last updated on 30/Aug/19

let A =∫_(−∞) ^(+∞) (dx/((x^2 −x+1)(x^2 +x+1))) and ϕ(z) =(1/((z^2 −z+1)(z^2 +z+1))) poles of ϕ? z^2 −z +1=0 →Δ =−3 =(i(√3))^2 ⇒ z_1 =((1+i(√3))/2) and z_2 =((1−i(√3))/2) z^2 +z +1=0 →Δ =−3 =(i(√3))^2 ⇒ α_1 =((−1+i(√3))/2) and α_2 =((−1−i(√3))/2) ϕ(z) = (1/((x−z_1 )(x−z_2 )(x−α_1 )(x−α_2 ))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,z_1 ) +Res(ϕ,α_1 )} Res (ϕ,z_1 ) =(1/((z_1 −z_2 )(z_1 ^2 +z_1 +1))) =(1/(i(√3)(z_1 ^2 +z_1 +1))) Res(ϕ,α_1 ) =(1/((α_1 −α_2 )(α_1 ^2 −α_1 +1))) =(1/(i(√3)(α_1 ^2 −α_1 +1))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{(1/(i(√3)(z_1 ^2 +z_1 +1))) +(1/(i(√3)(α_1 ^2 −α_1 +1)))} =((2π)/(√3)){ (1/(z_1 ^2 +z_1 +1)) +(1/(α_1 ^2 −α_1 +1))}

$${let}\:{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)} \\ $$$${and}\:\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −{z}+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+{z}+\mathrm{1}\right)}\:\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{2}} −{z}\:+\mathrm{1}=\mathrm{0}\:\rightarrow\Delta\:=−\mathrm{3}\:=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$${z}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{and}\:{z}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} +{z}\:+\mathrm{1}=\mathrm{0}\:\rightarrow\Delta\:=−\mathrm{3}\:=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\alpha_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{and}\:\alpha_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\varphi\left({z}\right)\:=\:\frac{\mathrm{1}}{\left({x}−{z}_{\mathrm{1}} \right)\left({x}−{z}_{\mathrm{2}} \right)\left({x}−\alpha_{\mathrm{1}} \right)\left({x}−\alpha_{\mathrm{2}} \right)} \\ $$$${residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:+{Res}\left(\varphi,\alpha_{\mathrm{1}} \right)\right\} \\ $$$${Res}\:\left(\varphi,{z}_{\mathrm{1}} \right)\:\:=\frac{\mathrm{1}}{\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)\left({z}_{\mathrm{1}} ^{\mathrm{2}} \:+{z}_{\mathrm{1}} +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}\left({z}_{\mathrm{1}} ^{\mathrm{2}} \:+{z}_{\mathrm{1}} +\mathrm{1}\right)} \\ $$$${Res}\left(\varphi,\alpha_{\mathrm{1}} \right)\:=\frac{\mathrm{1}}{\left(\alpha_{\mathrm{1}} −\alpha_{\mathrm{2}} \right)\left(\alpha_{\mathrm{1}} ^{\mathrm{2}} −\alpha_{\mathrm{1}} +\mathrm{1}\right)}\:=\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}\left(\alpha_{\mathrm{1}} ^{\mathrm{2}} −\alpha_{\mathrm{1}} +\mathrm{1}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}\left({z}_{\mathrm{1}} ^{\mathrm{2}} \:+{z}_{\mathrm{1}} +\mathrm{1}\right)}\:+\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}\left(\alpha_{\mathrm{1}} ^{\mathrm{2}} −\alpha_{\mathrm{1}} +\mathrm{1}\right)}\right\} \\ $$$$=\frac{\mathrm{2}\pi}{\sqrt{\mathrm{3}}}\left\{\:\:\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{1}} +\mathrm{1}}\:+\frac{\mathrm{1}}{\alpha_{\mathrm{1}} ^{\mathrm{2}} −\alpha_{\mathrm{1}} +\mathrm{1}}\right\} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com