calculate ∫_0 ^∞ (dx/((x^2 −e^(ia) )(x^2 −e^(ib) ))) with a>0 andb>0


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 67799 by mathmax by abdo last updated on 31/Aug/19

$c a l c u l a t e \int_{0}^{\infty} \frac{d x}{(x^{2} - e^{i a}) (x^{2} - e^{i b})} w i t h a > 0 a n d b > 0$
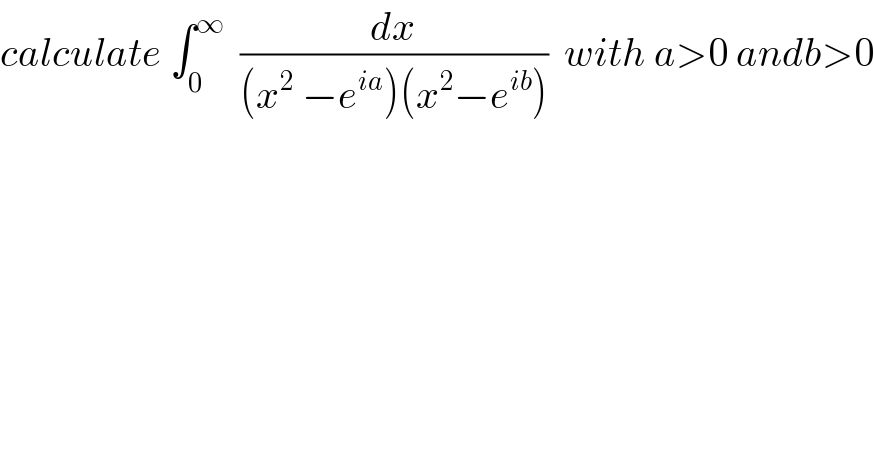
Commented byMJS last updated on 31/Aug/19

$can we calculate \underset{0}{\int^{\infty}} \frac{d x}{(x^{2} - α) (x^{2} - β)} and then$ $insert α = e^{i a}; β = e^{i b} ?$
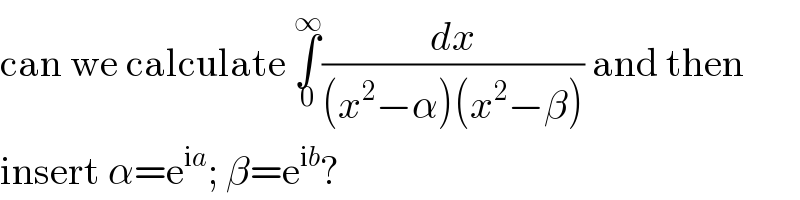
Commented bymathmax by abdo last updated on 31/Aug/19

$y e s s i r b u t y o u m u s t d e t e r m i n e \int \frac{d x}{x^{2} - z} w i t h z f r o m C .$
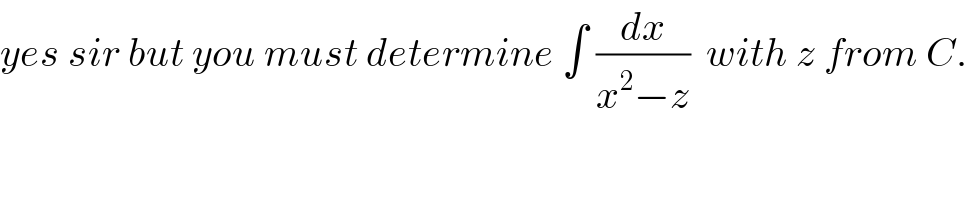
Commented bymathmax by abdo last updated on 01/Sep/19
$let I =∫_0 ^∞ (dx/((x^2 −e^(ia) )(x^2 −e^(ib) ))) ⇒2I =∫_(−∞) ^(+∞) (dx/((x^2 −e^(ia) )(x^2 −e^(ib) ))) let ϕ(z) =(1/((z^2 −e^(ia) )(z^2 −e^(ib) ))) ⇒ϕ(z) =(1/((z−e^((ia)/2) )(z+e^((ia)/2) )(z−e^((ib)/2) )(z+e^((ib)/2) ))) the poles of ϕ are +^− e^((ia)/2) and +^− e^((ib)/(2 )) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((ia)/2) )+Res(ϕ,e^((ib)/2) )} Res(ϕ,e^((ia)/2) )=lim_(z→e^((ia)/2) ) (z−e^((ia)/2) )ϕ(z) =(1/(2e^((ia)/2) (e^(ia) −e^(ib) ))) =(e^(−i(a/2)) /(2(e^(ia) −e^(ib) ))) Res(ϕ,e^((ib)/2) ) =lim_(z→e^((ib)/2) ) (z−e^((ib)/2) )ϕ(z) =(e^(−((ib)/2)) /(2(e^(ib) −e^(ia) ))) ⇒ ∫_(−∞) ^(+∞) ϕ(2)dz =2iπ{(e^(−((ia)/2)) /(2(e^(ia) −e^(ib) ))) +(e^(−((ib)/2)) /(2(e^(ib) −e^(ia) )))} =((iπ)/(e^(ia) −e^(ib) )){ e^(−((ia)/2)) −e^(−((ib)/2)) } =2I ⇒ I =((iπ(e^(−((ia)/2)) −e^(−((ib)/2)) ))/(2(e^(ia) −e^(ib) ))).$
$l e t I = \int_{0}^{\infty} \frac{d x}{(x^{2} - e^{i a}) (x^{2} - e^{i b})} \Rightarrow 2 I = \int_{- \infty}^{+ \infty} \frac{d x}{(x^{2} - e^{i a}) (x^{2} - e^{i b})}$ $l e t φ (z) = \frac{1}{(z^{2} - e^{i a}) (z^{2} - e^{i b})} \Rightarrow φ (z) = \frac{1}{(z - e^{\frac{i a}{2}}) (z + e^{\frac{i a}{2}}) (z - e^{\frac{i b}{2}}) (z + e^{\frac{i b}{2}})}$ $t h e p o l e s o f φ a r e \bar{+} e^{\frac{i a}{2}} a n d \bar{+} e^{\frac{i b}{2}} r e s i d u s t h e o r e m g i v e$ $\int_{- \infty}^{+ \infty} φ (z) d z = 2 i π {R e s (φ, e^{\frac{i a}{2}}) + R e s (φ, e^{\frac{i b}{2}})}$ $R e s (φ, e^{\frac{i a}{2}}) = {l i m}_{z \to e^{\frac{i a}{2}}} (z - e^{\frac{i a}{2}}) φ (z) = \frac{1}{2 e^{\frac{i a}{2}} (e^{i a} - e^{i b})} = \frac{e^{- i \frac{a}{2}}}{2 (e^{i a} - e^{i b})}$ $R e s (φ, e^{\frac{i b}{2}}) = {l i m}_{z \to e^{\frac{i b}{2}}} (z - e^{\frac{i b}{2}}) φ (z) = \frac{e^{- \frac{i b}{2}}}{2 (e^{i b} - e^{i a})} \Rightarrow$ $\int_{- \infty}^{+ \infty} φ (2) d z = 2 i π {\frac{e^{- \frac{i a}{2}}}{2 (e^{i a} - e^{i b})} + \frac{e^{- \frac{i b}{2}}}{2 (e^{i b} - e^{i a})}}$ $= \frac{i π}{e^{i a} - e^{i b}} {e^{- \frac{i a}{2}} - e^{- \frac{i b}{2}}} = 2 I \Rightarrow$ $I = \frac{i π (e^{- \frac{i a}{2}} - e^{- \frac{i b}{2}})}{2 (e^{i a} - e^{i b})} .$
	Answered by mind is power last updated on 01/Sep/19
	$let γ_r ={z∈C such that∣z∣≤r ∣im(z)>0} we have ∫_0 ^(+∞) (dx/((x^2 −e^(ia) )(x^2 −e^(ib) )))=(1/2)∫_(−∞) ^(+∞) (dx/((x^2 −e^(ia) )(x^2 −e^(ib) ))) let f(z)=(1/((z^2 −e^(ia) )(z^2 −e^(ib) ))) f(z)=(1/((r^2 e^(2i∅) −e^(ia) )(r^2 e^(2i∅) −e^(ib) ))) over γ_r ∣f(z)∣≤(1/(∣r^2 −1∣^2 )) we used ∣z+z′∣≥∣∣z∣−∣z′∣∣ twice ⇒∫_(γr) f(z)dz≤∫_γ_r (1/((r^2 −1)^2 ))dz=((πr)/((r^2 −1)^2 ))→0=as r→+∞ residu theorem poles of f inside γ_r ∪]−∞.+∞[ ar e^(i(a/2)) .e^((ib)/2) lim (z−e^(i(a/2)) ).f(z)=(1/(2e^(i(a/2)) .(e^(ia) −e^(ib) ))) lim(z−e^(i(b/2)) )f(z)=(1/(2e^(i(b/2)) (e^(ib) −e^(ia) ))) ∫_(−∞) ^(+∞) f(z)dz=2iπΣ_(residu) f(z)=2iπ((e^(−i(b/2)) /((e^(ib) −e^(ia) )2))−(e^(−((ia)/2)) /(2(e^(ib) −e^(ia) )))) =iπ(((e^(−((ib)/2)) −e^((−ia)/2) )/((e^(i((a+b)/2)) (e^(i((b−a)/2)) −e^(i−((b−a)/2)) ))))=iπ((e^(−ib−i(a/2)) −e^(−ia−i(b/2)) )/(2isin(((a−b)/2))))$
	$l e t γ_{r} = {z \in C s u c h t h a t ∣ z ∣⩽ r ∣ i m (z) > 0}$ $w e h a v e \int_{0}^{+ \infty} \frac{d x}{(x^{2} - e^{i a}) (x^{2} - e^{i b})} = \frac{1}{2} \int_{- \infty}^{+ \infty} \frac{d x}{(x^{2} - e^{i a}) (x^{2} - e^{i b})}$ $l e t f (z) = \frac{1}{(z^{2} - e^{i a}) (z^{2} - e^{i b})}$ $f (z) = \frac{1}{(r^{2} e^{2 i \emptyset} - e^{i a}) (r^{2} e^{2 i \emptyset} - e^{i b})} o v e r γ_{r}$ $∣ f (z) ∣⩽ \frac{1}{∣ r^{2} - 1 ∣^{2}}$ $w e u s e d ∣ z + z^{'} ∣⩾∣∣ z ∣ - ∣ z^{'} ∣∣ t w i c e$ $\Rightarrow \int_{γ r} f (z) d z ⩽ \int_{γ_{r}} \frac{1}{{(r^{2} - 1)}^{2}} d z = \frac{π r}{{(r^{2} - 1)}^{2}} \to 0 = a s r \to + \infty$ $r e s i d u t h e o r e m$ $p o l e s o f f i n s i d e γ_{r} \cup] - \infty . + \infty [a r e^{i \frac{a}{2}} . e^{\frac{i b}{2}}$ $l i m (z - e^{i \frac{a}{2}}) . f (z) = \frac{1}{2 e^{i \frac{a}{2}} . (e^{i a} - e^{i b})}$ $l i m (z - e^{i \frac{b}{2}}) f (z) = \frac{1}{2 e^{i \frac{b}{2}} (e^{i b} - e^{i a})}$ $\int_{- \infty}^{+ \infty} f (z) d z = 2 i π \sum_{r e s i d u} f (z) = 2 i π (\frac{e^{- i \frac{b}{2}}}{(e^{i b} - e^{i a}) 2} - \frac{e^{- \frac{i a}{2}}}{2 (e^{i b} - e^{i a})})$ $= i π (\frac{e^{- \frac{i b}{2}} - e^{\frac{- i a}{2}}}{(e^{i \frac{a + b}{2}} (e^{i \frac{b - a}{2}} - e^{i - \frac{b - a}{2}})}) = i π \frac{e^{- i b - i \frac{a}{2}} - e^{- i a - i \frac{b}{2}}}{2 i s i n (\frac{a - b}{2})}$
	Commented bymathmax by abdo last updated on 01/Sep/19

	$t h a n k y o u s i r .$
	Commented bymind is power last updated on 01/Sep/19

	$y : r e w e l c o m$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum