Question and Answers Forum
Question Number 67851 by mathmax by abdo last updated on 01/Sep/19
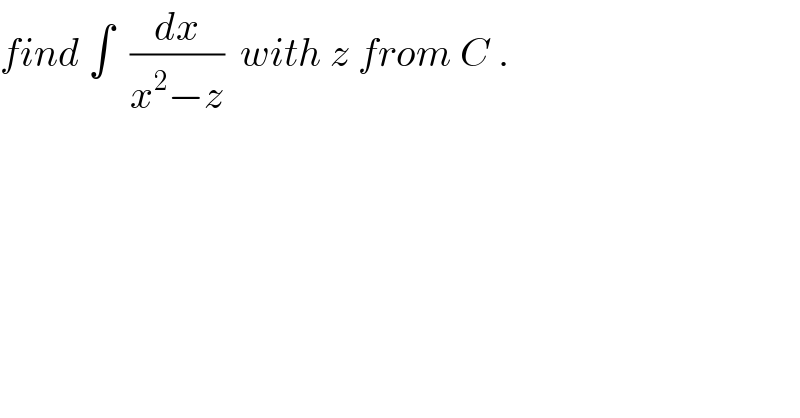
Commented by MJS last updated on 01/Sep/19
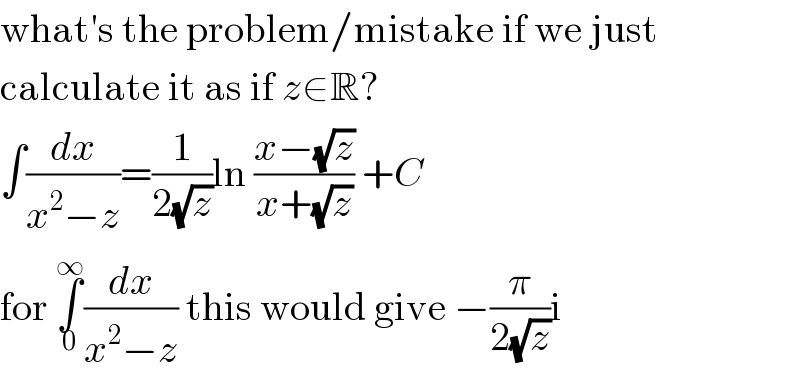
Commented by mathmax by abdo last updated on 01/Sep/19
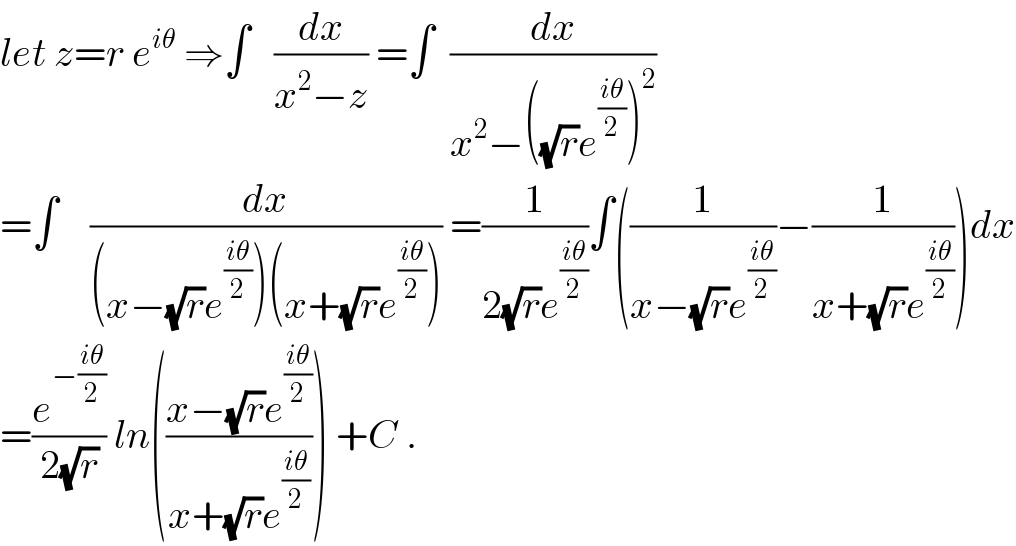
Commented by mathmax by abdo last updated on 01/Sep/19
Commented by mathmax by abdo last updated on 01/Sep/19
![∫_0 ^∞ (dx/(x^2 −z)) =(e^(−((iθ)/2)) /(2(√r)))[ln(((x−(√r)e^((iθ)/2) )/(x+(√r)e^((iθ)/2) )))]_0 ^(+∞) =(e^(−((iθ)/2)) /(2(√r)))(−ln(−1)) =((iπ)/(2(2(√r))e^((iθ)/2) )) =((iπ)/(4(√r)e^((iθ)/2) )) with z =r e^(iθ) .](Q67896.png)
Commented by MJS last updated on 01/Sep/19