Question Number 67932 by mathmax by abdo last updated on 02/Sep/19
$${let}\:{A}\left(\theta\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)}\:\:{with}\:\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}} \\ $$ $$\left.\mathrm{1}\right)\:{calculate}\:{A}\left(\theta\right)\:{interms}\:{of}\:\theta \\ $$ $$\left.\mathrm{2}\right)\:{determine}\:{also}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)^{\mathrm{2}} } \\ $$
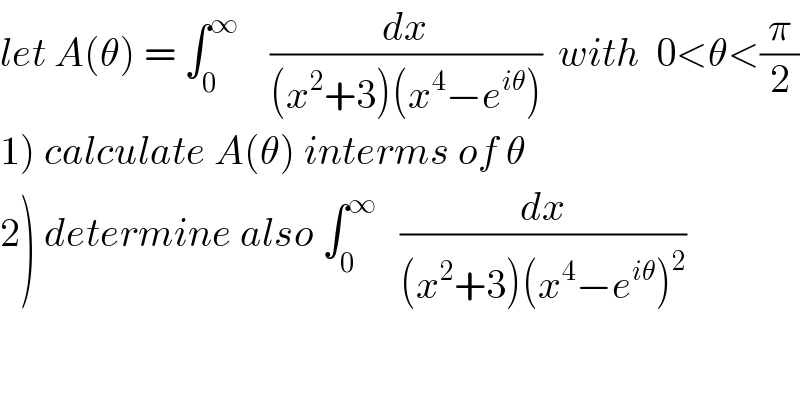
Commented byMJS last updated on 02/Sep/19
$$\mathrm{I}\:\mathrm{get}\:\left(\mathrm{1}\right)\:\:{A}\left(\theta\right)=−\frac{\pi\left(\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{\mathrm{i}\frac{\mathrm{3}\theta}{\mathrm{4}}} −\mathrm{3e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} −\mathrm{9}\right)}{\mathrm{12e}^{\mathrm{i}\frac{\mathrm{3}\theta}{\mathrm{4}}} \left(\mathrm{e}^{\mathrm{i}\theta} −\mathrm{9}\right)} \\ $$ $$\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{right}? \\ $$
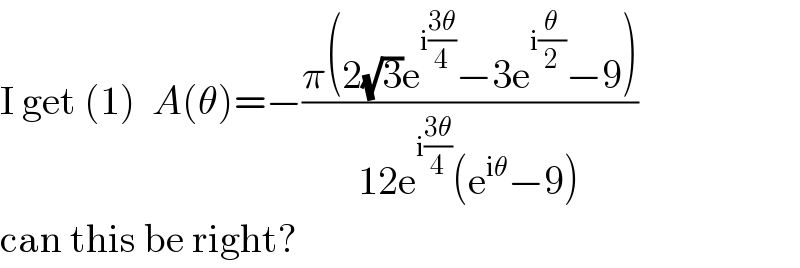
Commented bymathmax by abdo last updated on 02/Sep/19
![1) A(θ)=∫_0 ^∞ (dx/((x^2 +3)(x^4 −e^(iθ) ))) ⇒2A(θ)=∫_(−∞) ^(+∞) (dx/((x^2 +3)(x^4 −e^(iθ) ))) let W(z) =(1/((z^2 +3)(z^4 −e^(iθ) ))) poles of W? z^4 −e^(iθ) =0 ⇒z^4 =e^(iθ) let z =r e^(iα) ⇒r=1 and 4α =θ +2kπ ⇒ α_k =((θ+2kπ)/4) ⇒ the roots are Z_k =e^(i((θ+2kπ)/4)) and k∈[[0,3]] Z_0 =e^((iθ)/4) ,Z_1 =e^(i(((θ+2π)/4))) =e^(((iθ)/4)+((iπ)/2)) , Z_2 =e^(i(((θ+4π)/4))) =e^(((iθ)/4)+iπ) Z_3 = e^(i(((θ+6π)/4))) =e^(((iθ)/4)+i((3π)/2)) =e^(((iθ)/4)+i(2π−(π/2))) =e^(i((θ/4)−(π/2))) Z_1 =i e^((iπ)/4) =i{cos((π/4))+isin((π/4))}=−sin(π/4)+icos((π/4))⇒im(z_1 )>0 im(Z_0 )>0 im(Z_2 )<0 im(z_3 )<0 z^2 +3 =z^2 −(i(√3))^2 =(z−i(√3))(z+i(√3)) so the roots are +^− i(√3) residu theorem ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ{Res(W,i(√3)) +Res(W,Z_0 )+Res(W,Z_1 )} we have W(z) =(1/((z−i(√3))(z+i(√3))(z−Z_0 )(z−Z_1 )(z−Z_2 )(z−Z_3 ))) ⇒ Res(W,i(√3)) =(1/((2i(√3))((i(√3))^4 −e^(iθ) ))) =(1/((2i(√3))(9−e^(iθ) ))) Res(W,Z_0 ) =(1/((Z_0 ^2 +3)(Z_0 −Z_1 )(Z_0 −Z_2 )(Z_0 −Z_3 ))) Res(W,Z_1 ) =(1/((Z_1 ^2 +3)(Z_1 −Z_0 )(Z_1 −Z_2 )(Z_1 −Z_3 ))) rest to finich the calculus ....](Q67980.png)
$$\left.\mathrm{1}\right)\:{A}\left(\theta\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)}\:\Rightarrow\mathrm{2}{A}\left(\theta\right)=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)} \\ $$ $${let}\:{W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{3}\right)\left({z}^{\mathrm{4}} −{e}^{{i}\theta} \right)}\:\:{poles}\:{of}\:{W}? \\ $$ $${z}^{\mathrm{4}} −{e}^{{i}\theta} \:=\mathrm{0}\:\Rightarrow{z}^{\mathrm{4}} ={e}^{{i}\theta} \:\:\:\:\:{let}\:{z}\:={r}\:{e}^{{i}\alpha} \:\Rightarrow{r}=\mathrm{1}\:{and}\:\mathrm{4}\alpha\:=\theta\:+\mathrm{2}{k}\pi\:\Rightarrow \\ $$ $$\alpha_{{k}} =\frac{\theta+\mathrm{2}{k}\pi}{\mathrm{4}}\:\:\Rightarrow\:{the}\:{roots}\:{are}\:{Z}_{{k}} ={e}^{{i}\frac{\theta+\mathrm{2}{k}\pi}{\mathrm{4}}} \:\:{and}\:{k}\in\left[\left[\mathrm{0},\mathrm{3}\right]\right] \\ $$ $${Z}_{\mathrm{0}} ={e}^{\frac{{i}\theta}{\mathrm{4}}} \:\:\:\:,{Z}_{\mathrm{1}} ={e}^{{i}\left(\frac{\theta+\mathrm{2}\pi}{\mathrm{4}}\right)} ={e}^{\frac{{i}\theta}{\mathrm{4}}+\frac{{i}\pi}{\mathrm{2}}} \:\:,\:{Z}_{\mathrm{2}} ={e}^{{i}\left(\frac{\theta+\mathrm{4}\pi}{\mathrm{4}}\right)} ={e}^{\frac{{i}\theta}{\mathrm{4}}+{i}\pi} \\ $$ $${Z}_{\mathrm{3}} \:\:=\:{e}^{{i}\left(\frac{\theta+\mathrm{6}\pi}{\mathrm{4}}\right)} \:={e}^{\frac{{i}\theta}{\mathrm{4}}+{i}\frac{\mathrm{3}\pi}{\mathrm{2}}} ={e}^{\frac{{i}\theta}{\mathrm{4}}+{i}\left(\mathrm{2}\pi−\frac{\pi}{\mathrm{2}}\right)} ={e}^{{i}\left(\frac{\theta}{\mathrm{4}}−\frac{\pi}{\mathrm{2}}\right)} \\ $$ $${Z}_{\mathrm{1}} ={i}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:={i}\left\{{cos}\left(\frac{\pi}{\mathrm{4}}\right)+{isin}\left(\frac{\pi}{\mathrm{4}}\right)\right\}=−{sin}\frac{\pi}{\mathrm{4}}+{icos}\left(\frac{\pi}{\mathrm{4}}\right)\Rightarrow{im}\left({z}_{\mathrm{1}} \right)>\mathrm{0} \\ $$ $${im}\left({Z}_{\mathrm{0}} \right)>\mathrm{0}\:\:{im}\left({Z}_{\mathrm{2}} \right)<\mathrm{0}\:\:{im}\left({z}_{\mathrm{3}} \right)<\mathrm{0} \\ $$ $${z}^{\mathrm{2}} +\mathrm{3}\:={z}^{\mathrm{2}} −\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:=\left({z}−{i}\sqrt{\mathrm{3}}\right)\left({z}+{i}\sqrt{\mathrm{3}}\right)\:{so}\:{the}\:{roots}\:{are}\:\overset{−} {+}{i}\sqrt{\mathrm{3}} \\ $$ $${residu}\:{theorem}\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{{Res}\left({W},{i}\sqrt{\mathrm{3}}\right)\right. \\ $$ $$\left.+{Res}\left({W},{Z}_{\mathrm{0}} \right)+{Res}\left({W},{Z}_{\mathrm{1}} \right)\right\}\:{we}\:{have} \\ $$ $${W}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{i}\sqrt{\mathrm{3}}\right)\left({z}+{i}\sqrt{\mathrm{3}}\right)\left({z}−{Z}_{\mathrm{0}} \right)\left({z}−{Z}_{\mathrm{1}} \right)\left({z}−{Z}_{\mathrm{2}} \right)\left({z}−{Z}_{\mathrm{3}} \right)}\:\Rightarrow \\ $$ $${Res}\left({W},{i}\sqrt{\mathrm{3}}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}\right)\left(\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{4}} −{e}^{{i}\theta} \right)}\:=\frac{\mathrm{1}}{\left(\mathrm{2}{i}\sqrt{\mathrm{3}}\right)\left(\mathrm{9}−{e}^{{i}\theta} \right)} \\ $$ $${Res}\left({W},{Z}_{\mathrm{0}} \right)\:=\frac{\mathrm{1}}{\left({Z}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{3}\right)\left({Z}_{\mathrm{0}} −{Z}_{\mathrm{1}} \right)\left({Z}_{\mathrm{0}} −{Z}_{\mathrm{2}} \right)\left({Z}_{\mathrm{0}} −{Z}_{\mathrm{3}} \right)} \\ $$ $${Res}\left({W},{Z}_{\mathrm{1}} \right)\:=\frac{\mathrm{1}}{\left({Z}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{3}\right)\left({Z}_{\mathrm{1}} −{Z}_{\mathrm{0}} \right)\left({Z}_{\mathrm{1}} −{Z}_{\mathrm{2}} \right)\left({Z}_{\mathrm{1}} −{Z}_{\mathrm{3}} \right)} \\ $$ $${rest}\:{to}\:{finich}\:{the}\:{calculus}\:.... \\ $$ $$ \\ $$
Commented bymathmax by abdo last updated on 02/Sep/19
$${perhaps}\:{because}\:{i}\:{dont}\:{complete}\:{the}\:{calculus}.. \\ $$
Commented bymathmax by abdo last updated on 02/Sep/19
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{A}^{'} \left(\theta\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{{i}\theta} }{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)^{\mathrm{2}} }\:={e}^{−{i}\theta} \:{A}^{'} \left(\theta\right)\:\:{rest}\:{to}\:{calculate}\:\:{A}^{'} \left(\theta\right). \\ $$
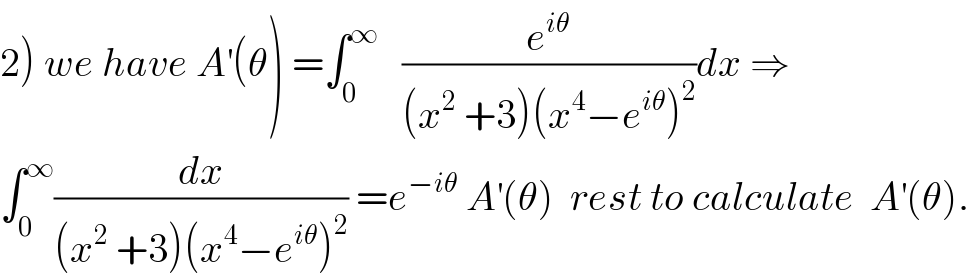
Answered by mind is power last updated on 02/Sep/19
![let f(z)=(dz/((z^2 +3)(x^4 −e^(iθ) ))) pole of f are +_− i(√3) ,e^(i((θ+2kπ)/4)) k≤4 we shose uper[half im(z)>0 plan and use residus theorem Res (f.i(√3))=(1/(2i(√3) (9−e^(iθ) ))) res (f,e^(iθ) )=(1/(4e^(i3θ) (e^(2iθ) +3))) res (f,e^(i(θ+(π/2))) )=(1/(4e^(i(3θ+((3π)/2))) (−e^(i2θ) +3))) ∫_0 ^(+∞) (dz/((z^2 +3)(z^4 +e^(iθ) )))=(1/2)∫_(−∞) ^(+∞) f(z)dz=iπΣ_(res >0 ) f(z) =iπ[(1/(2i(√3)(9−e^(iθ) )))+(1/(4e^(3iθ) (e^(2iθ) +3)))+(1/(−4ie^(3iθ) (3−e^(2iθ) )))] =((iπ)/)[((−i(9−e^(−iθ) ))/(2(√3)(82−18cos(θ))))+((e^(−3iθ) (3+e^(−2iθ) ))/(4(10+6cos(2θ))))+((ie^(−i3θ) (3−e^(−2iθ) ))/(4(10−6cos(2θ)))) ) 2) (df/dθ)=∫(e^(iθ) /((z^2 +3)(z^4 −e^(iθ) )^2 ))dz=e^(iθ) ∫(1/((z^2 +3)(z^4 −e^(iθ) )))dz ⇒∫(dx/((x^2 +3)(x^4 −e^(iθ) )))=f′(θ)e^(−iθ)](Q67967.png)
$${let}\:{f}\left({z}\right)=\frac{{dz}}{\left({z}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)} \\ $$ $${pole}\:{of}\:{f}\:{are}\:\underset{−} {+}{i}\sqrt{\mathrm{3}}\:\:,{e}^{{i}\frac{\theta+\mathrm{2}{k}\pi}{\mathrm{4}}} \:\:\:\:{k}\leqslant\mathrm{4} \\ $$ $${we}\:{shose}\:{uper}\left[{half}\:{im}\left({z}\right)>\mathrm{0}\:\:{plan}\:{and}\:\:{use}\:{residus}\:{theorem}\right. \\ $$ $${Res}\:\left({f}.{i}\sqrt{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\:\left(\mathrm{9}−{e}^{{i}\theta} \right)} \\ $$ $${res}\:\left({f},{e}^{{i}\theta} \right)=\frac{\mathrm{1}}{\mathrm{4}{e}^{{i}\mathrm{3}\theta} \left({e}^{\mathrm{2}{i}\theta} +\mathrm{3}\right)} \\ $$ $${res}\:\left({f},{e}^{{i}\left(\theta+\frac{\pi}{\mathrm{2}}\right)} \right)=\frac{\mathrm{1}}{\mathrm{4}{e}^{{i}\left(\mathrm{3}\theta+\frac{\mathrm{3}\pi}{\mathrm{2}}\right)} \left(−{e}^{{i}\mathrm{2}\theta} +\mathrm{3}\right)} \\ $$ $$\int_{\mathrm{0}} ^{+\infty} \frac{{dz}}{\left({z}^{\mathrm{2}} +\mathrm{3}\right)\left({z}^{\mathrm{4}} +{e}^{{i}\theta} \right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}={i}\pi\sum_{{res}\:>\mathrm{0}\:} {f}\left({z}\right) \\ $$ $$={i}\pi\left[\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\left(\mathrm{9}−{e}^{{i}\theta} \right)}+\frac{\mathrm{1}}{\mathrm{4}{e}^{\mathrm{3}{i}\theta} \left({e}^{\mathrm{2}{i}\theta} +\mathrm{3}\right)}+\frac{\mathrm{1}}{−\mathrm{4}{ie}^{\mathrm{3}{i}\theta} \left(\mathrm{3}−{e}^{\mathrm{2}{i}\theta} \right)}\right] \\ $$ $$=\frac{{i}\pi}{}\left[\frac{−{i}\left(\mathrm{9}−{e}^{−{i}\theta} \right)}{\mathrm{2}\sqrt{\mathrm{3}}\left(\mathrm{82}−\mathrm{18}{cos}\left(\theta\right)\right)}+\frac{{e}^{−\mathrm{3}{i}\theta} \left(\mathrm{3}+{e}^{−\mathrm{2}{i}\theta} \right)}{\mathrm{4}\left(\mathrm{10}+\mathrm{6}{cos}\left(\mathrm{2}\theta\right)\right)}+\frac{{ie}^{−{i}\mathrm{3}\theta} \left(\mathrm{3}−{e}^{−\mathrm{2}{i}\theta} \right)}{\mathrm{4}\left(\mathrm{10}−\mathrm{6}{cos}\left(\mathrm{2}\theta\right)\right)}\:\right) \\ $$ $$\left.\mathrm{2}\right)\:\frac{{df}}{{d}\theta}=\int\frac{{e}^{{i}\theta} }{\left({z}^{\mathrm{2}} +\mathrm{3}\right)\left({z}^{\mathrm{4}} −{e}^{{i}\theta} \right)^{\mathrm{2}} }{dz}={e}^{{i}\theta} \int\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} +\mathrm{3}\right)\left({z}^{\mathrm{4}} −{e}^{{i}\theta} \right)}{dz} \\ $$ $$\Rightarrow\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{3}\right)\left({x}^{\mathrm{4}} −{e}^{{i}\theta} \right)}={f}'\left(\theta\right){e}^{−{i}\theta} \\ $$ $$ \\ $$ $$ \\ $$