
Previous in Relation and Functions Next in Relation and Functions
Question Number 67972 by mathmax by abdo last updated on 02/Sep/19
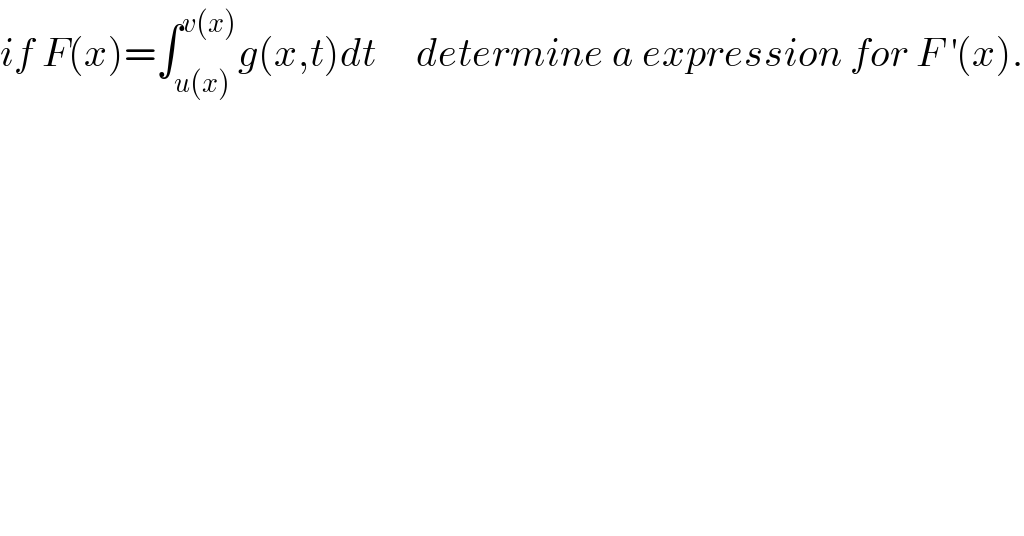
$${if}\:{F}\left({x}\right)=\int_{{u}\left({x}\right)} ^{{v}\left({x}\right)} {g}\left({x},{t}\right){dt}\:\:\:\:\:{determine}\:{a}\:{expression}\:{for}\:{F}\:^{'} \left({x}\right). \\ $$
Answered by Tanmay chaudhury last updated on 03/Sep/19
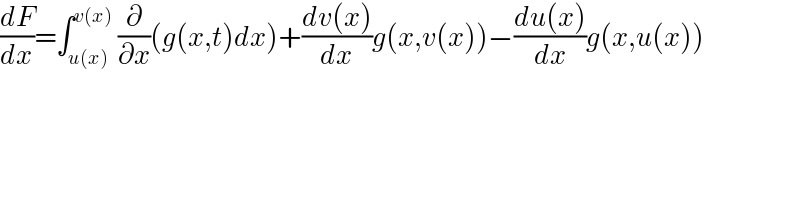
$$\frac{{dF}}{{dx}}=\int_{{u}\left({x}\right)} ^{{v}\left({x}\right)} \:\frac{\partial}{\partial{x}}\left({g}\left({x},{t}\right){dx}\right)+\frac{{dv}\left({x}\right)}{{dx}}{g}\left({x},{v}\left({x}\right)\right)−\frac{{du}\left({x}\right)}{{dx}}{g}\left({x},{u}\left({x}\right)\right) \\ $$
Commented by mathmax by abdo last updated on 03/Sep/19
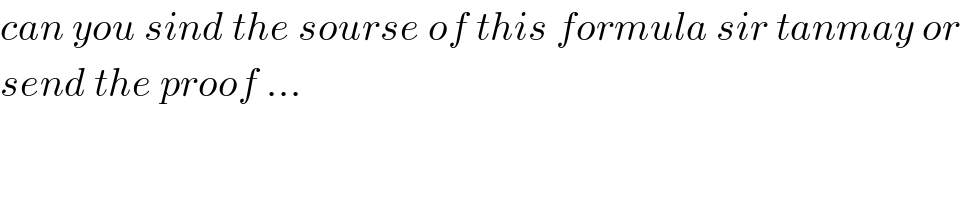
$${can}\:{you}\:{sind}\:{the}\:{sourse}\:{of}\:{this}\:{formula}\:{sir}\:{tanmay}\:{or}\: \\ $$$${send}\:{the}\:{proof}\:... \\ $$
Commented by Tanmay chaudhury last updated on 03/Sep/19

$${ok}\:{sir}... \\ $$
Commented by mind is power last updated on 03/Sep/19
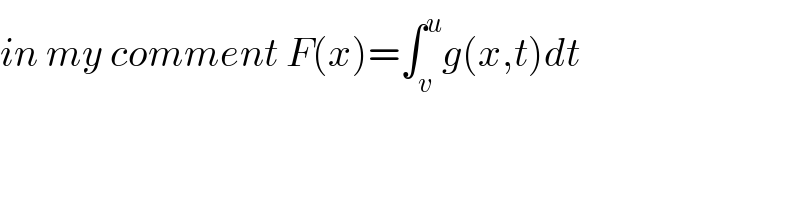
$${in}\:{my}\:{comment}\:{F}\left({x}\right)=\int_{{v}} ^{{u}} {g}\left({x},{t}\right){dt} \\ $$
Commented by mathmax by abdo last updated on 03/Sep/19
![let verify this formulae by F(x) =∫_x ^x^2 e^(−xt) dt we have g(x,t) =e^(−xt) , u(x)=x and v(x)=x^2 gormulae give F^′ (x) =∫_(u(x)) ^(v(x)) (∂g/∂x)(x,t)dt +v^′ g(x,v)−u^′ g(x,u) =∫_x ^x^2 −t e^(−xt) dt +(2x)e^(−x^3 ) −e^(−x^2 ) by partswe get ∫_x ^x^2 t e^(−xt) dt =[−(t/x)e^(−xt) ]_x ^x^2 −∫_x ^x^2 (−(1/x))e^(−xt) dt =e^(−x^2 ) −x e^(−x^3 ) +(1/x) ∫_x ^x^2 e^(−xt) dt =e^(−x^2 ) −x e^(−x^3 ) +(1/x)[−(1/x)e^(−xt) ]_x ^x^2 =e^(−x^2 ) −xe^(−x^3 ) −(1/x^2 ){ e^(−x^3 ) −e^(−x^2 ) } =(1+(1/x^2 ))e^(−x^2 ) −(x+(1/x^2 ))e^(−x^3 ) ⇒F^′ (x) =−(1+(1/x^2 ))e^(−x^2 ) +(x+(1/x^2 ))e^(−x^3 ) +2x e^(−x^3 ) −e^(−x^2 ) =−(2+(1/x^2 ) )e^(−x^2 ) (3x+(1/x^2 ))e^(−x^3 ) now let find F(x) directly F(x) =[−(1/x)e^(−xt) ]_x ^x^2 =−(1/x){ e^(−x^3 ) −e^(−x^2 ) } =(1/x){e^(−x^2 ) −e^(−x^3 ) } ⇒ F^′ (x) =−(1/x^2 ){ e^(−x^2 ) −e^(−x^3 ) } +(1/x){−2x e^(−x^2 ) +3x^2 e^(−x^3 ) } =−(1/x^2 )e^(−x^2 ) +(1/x^2 )e^(−x^3 ) −2e^(−x^2 ) +3x e^(−x^3 ) =−((1/x^2 ) +2)e^(−x^2 ) +(3x+(1/x^2 ))e^(−x^2 ) we get the same result so the formulae is correct .](Q68014.png)
$${let}\:{verify}\:{this}\:{formulae}\:{by}\:\:{F}\left({x}\right)\:=\int_{{x}} ^{{x}^{\mathrm{2}} } {e}^{−{xt}} {dt}\:{we}\:{have} \\ $$$${g}\left({x},{t}\right)\:={e}^{−{xt}} \:\:\:,\:{u}\left({x}\right)={x}\:\:{and}\:{v}\left({x}\right)={x}^{\mathrm{2}} \:\:{gormulae}\:{give} \\ $$$${F}\:^{'} \left({x}\right)\:=\int_{{u}\left({x}\right)} ^{{v}\left({x}\right)} \frac{\partial{g}}{\partial{x}}\left({x},{t}\right){dt}\:\:+{v}^{'} {g}\left({x},{v}\right)−{u}^{'} {g}\left({x},{u}\right) \\ $$$$=\int_{{x}} ^{{x}^{\mathrm{2}} } \:−{t}\:{e}^{−{xt}} \:{dt}\:\:+\left(\mathrm{2}{x}\right){e}^{−{x}^{\mathrm{3}} } −{e}^{−{x}^{\mathrm{2}} } \:\:\:{by}\:{partswe}\:{get} \\ $$$$\int_{{x}} ^{{x}^{\mathrm{2}} } {t}\:{e}^{−{xt}} \:{dt}\:=\left[−\frac{{t}}{{x}}{e}^{−{xt}} \right]_{{x}} ^{{x}^{\mathrm{2}} } −\int_{{x}} ^{{x}^{\mathrm{2}} } \left(−\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)\boldsymbol{{e}}^{−\boldsymbol{{xt}}} \boldsymbol{{dt}} \\ $$$$=\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } −\boldsymbol{{x}}\:\boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{3}} } \:+\frac{\mathrm{1}}{\boldsymbol{{x}}}\:\int_{{x}} ^{{x}^{\mathrm{2}} } {e}^{−{xt}} {dt}\:={e}^{−{x}^{\mathrm{2}} } −{x}\:{e}^{−{x}^{\mathrm{3}} } +\frac{\mathrm{1}}{{x}}\left[−\frac{\mathrm{1}}{{x}}{e}^{−{xt}} \right]_{{x}} ^{{x}^{\mathrm{2}} } \\ $$$$={e}^{−{x}^{\mathrm{2}} } −{xe}^{−{x}^{\mathrm{3}} } −\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left\{\:\:{e}^{−{x}^{\mathrm{3}} } −{e}^{−{x}^{\mathrm{2}} } \right\} \\ $$$$=\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{2}} } −\left({x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{3}} \:} \:\Rightarrow{F}\:^{'} \left({x}\right)\:=−\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{2}} } +\left({x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{3}} } \\ $$$$+\mathrm{2}{x}\:{e}^{−{x}^{\mathrm{3}} } −{e}^{−{x}^{\mathrm{2}} } \:=−\left(\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\right){e}^{−{x}^{\mathrm{2}} } \left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{3}} } \:{now}\:{let}\:{find}\:{F}\left({x}\right)\:{directly} \\ $$$${F}\left({x}\right)\:=\left[−\frac{\mathrm{1}}{{x}}{e}^{−{xt}} \right]_{{x}} ^{{x}^{\mathrm{2}} } \:=−\frac{\mathrm{1}}{{x}}\left\{\:{e}^{−{x}^{\mathrm{3}} } −{e}^{−{x}^{\mathrm{2}} } \right\}\:=\frac{\mathrm{1}}{{x}}\left\{{e}^{−{x}^{\mathrm{2}} } −{e}^{−{x}^{\mathrm{3}} } \right\}\:\Rightarrow \\ $$$${F}\:^{'} \left({x}\right)\:=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left\{\:{e}^{−{x}^{\mathrm{2}} } −{e}^{−{x}^{\mathrm{3}} } \right\}\:+\frac{\mathrm{1}}{{x}}\left\{−\mathrm{2}{x}\:{e}^{−{x}^{\mathrm{2}} } +\mathrm{3}{x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{3}} } \right\} \\ $$$$=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{e}^{−{x}^{\mathrm{2}} } +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{e}^{−{x}^{\mathrm{3}} } −\mathrm{2}{e}^{−{x}^{\mathrm{2}} } \:\:+\mathrm{3}{x}\:{e}^{−{x}^{\mathrm{3}} } \\ $$$$=−\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\mathrm{2}\right){e}^{−{x}^{\mathrm{2}} } \:\:+\left(\mathrm{3}{x}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){e}^{−{x}^{\mathrm{2}} } \:\:\:\:\:{we}\:{get}\:{the}\:{same}\:{result} \\ $$$${so}\:{the}\:{formulae}\:{is}\:{correct}\:. \\ $$
Answered by mind is power last updated on 03/Sep/19
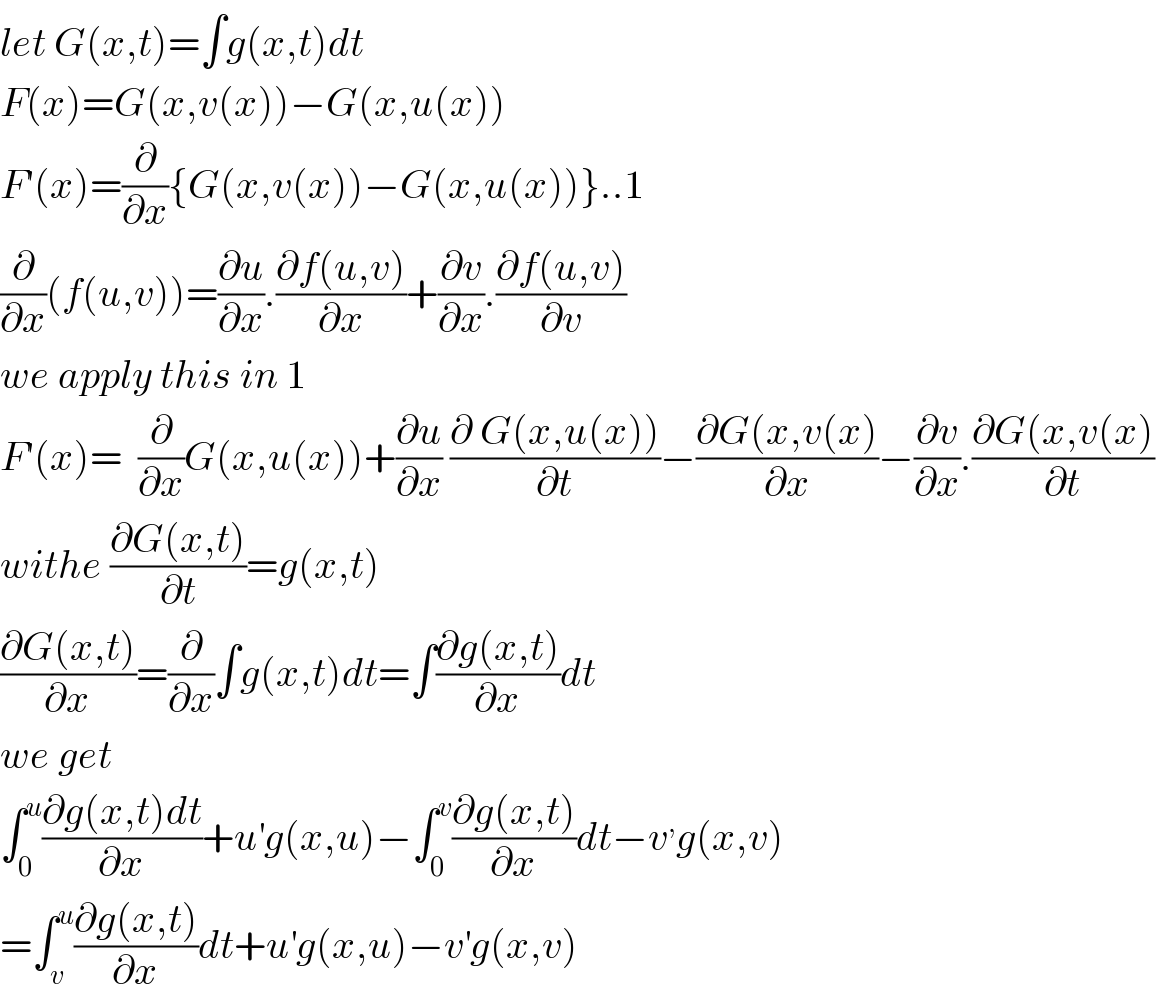
$${let}\:{G}\left({x},{t}\right)=\int{g}\left({x},{t}\right){dt} \\ $$$${F}\left({x}\right)={G}\left({x},{v}\left({x}\right)\right)−{G}\left({x},{u}\left({x}\right)\right) \\ $$$${F}'\left({x}\right)=\frac{\partial}{\partial{x}}\left\{{G}\left({x},{v}\left({x}\right)\right)−{G}\left({x},{u}\left({x}\right)\right)\right\}..\mathrm{1} \\ $$$$\frac{\partial}{\partial{x}}\left({f}\left({u},{v}\right)\right)=\frac{\partial{u}}{\partial{x}}.\frac{\partial{f}\left({u},{v}\right)}{\partial{x}}+\frac{\partial{v}}{\partial{x}}.\frac{\partial{f}\left({u},{v}\right)}{\partial{v}} \\ $$$${we}\:{apply}\:{this}\:{in}\:\mathrm{1} \\ $$$${F}'\left({x}\right)=\:\:\frac{\partial}{\partial{x}}{G}\left({x},{u}\left({x}\right)\right)+\frac{\partial{u}}{\partial{x}}\:\frac{\partial\:{G}\left({x},{u}\left({x}\right)\right)}{\partial{t}}−\frac{\partial{G}\left({x},{v}\left({x}\right)\right.}{\partial{x}}−\frac{\partial{v}}{\partial{x}}.\frac{\partial{G}\left({x},{v}\left({x}\right)\right.}{\partial{t}}\:\: \\ $$$${withe}\:\frac{\partial{G}\left({x},{t}\right)}{\partial{t}}={g}\left({x},{t}\right) \\ $$$$\frac{\partial{G}\left({x},{t}\right)}{\partial{x}}=\frac{\partial}{\partial{x}}\int{g}\left({x},{t}\right){dt}=\int\frac{\partial{g}\left({x},{t}\right)}{\partial{x}}{dt} \\ $$$${we}\:{get}\: \\ $$$$\int_{\mathrm{0}} ^{{u}} \frac{\partial{g}\left({x},{t}\right){dt}}{\partial{x}}+{u}^{'} {g}\left({x},{u}\right)−\int_{\mathrm{0}} ^{{v}} \frac{\partial{g}\left({x},{t}\right)}{\partial{x}}{dt}−{v}^{,} {g}\left({x},{v}\right) \\ $$$$=\int_{{v}} ^{{u}} \frac{\partial{g}\left({x},{t}\right)}{\partial{x}}{dt}+{u}^{'} {g}\left({x},{u}\right)−{v}^{'} {g}\left({x},{v}\right) \\ $$
Commented by mathmax by abdo last updated on 10/Sep/19

$${thank}\:{you}\:{sir}. \\ $$
