Question Number 68100 by ~ À ® @ 237 ~ last updated on 04/Sep/19
$${Find}\:\:{K}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}−{t}+{t}^{\mathrm{2}} \right)}{{t}}\:{dt}\:\:\:\:\: \\ $$
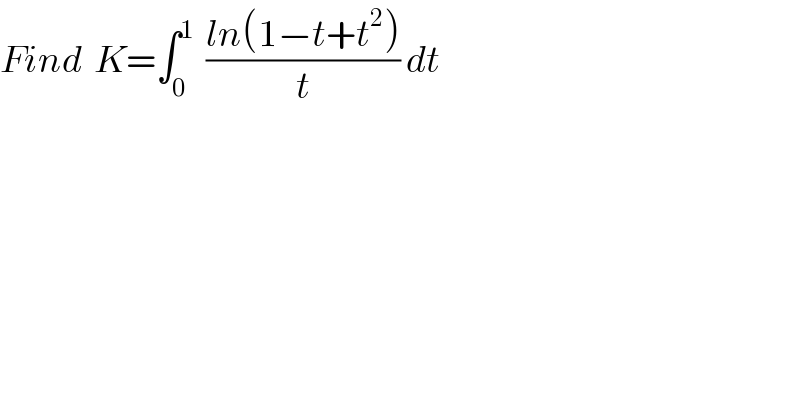
Commented by mind is power last updated on 05/Sep/19
$${y},{re}\:{welcom} \\ $$
Commented by mind is power last updated on 05/Sep/19
![f(s)=∫_0 ^1 ((ln(1−(t−t^2 )s))/t) s∈[0,1] f′(s)=∫_0 ^1 ((−(t−t^2 ))/(t(1−(t−t^2 )s)))dt =∫_0 ^1 ((t−1)/(1−(t−t^2 )s))dt ∫_0 ^1 ((t−1)/(t^2 s−ts+1))dt =∫_0 ^1 ((t−(1/2))/(t^2 s−ts+1))−(1/2)∫_0 ^1 (1/(t^2 s−ts+1))dt =(1/(2s))[ln(t^2 s−ts+1)]_0 ^1 −(1/(2s))∫_0 ^1 (dt/(t^2 −t+(1/s))) −(1/(2s))∫_0 ^1 (dt/((t−(1/2))^2 +(1/s)−(1/4))) −(2/(4−s))∫_0 ^1 (dt/({((t−(1/2)).(√((4s)/(4−s))))^2 +1}.)) =−(1/(√(s(4−s))))[arctan((t−(1/2))(√((4s)/(4−s))))]_0 ^1 =−(2/(√(s(4−s))))[arctg((√(s/(4−s))))] f(s)=∫−(2/(√(s(4−s))))arctan((√(s/(4−s))))ds let u=(√(s/(4−s)))⇒s=((4u^2 )/(u^2 +1)) ds=((8u)/((1+u^2 )^2 ))du s(4−s)=((16u^2 )/((u^2 +1)^2 )) ∫((−2)/(√(s(4−s))))[arctan((√((4s)/(4−s))))]ds =∫((−2)/(√((16u^2 )/((u^2 +1)^2 )))).arctan(u).((8u)/((1+u^2 )^2 )) =∫((−2(u^2 +1))/(4u))arctan(u).((8u)/((1+u^2 )))du =∫((−4)/(1+u^2 ))arctan(u)du =−2(arctan(u))^2 +c =−2(arctan((√(s/(4−s)))))^2 +c=f(s) f(0)=0=>c=0 f(s)=−2(arctan((√(s/(4−s)))))^2 k=f(1)=−2(arctan((1/(√3))))^2 =−2((π/6))^2 =((−π^2 )/(18))](Q68105.png)
$${f}\left({s}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\left({t}−{t}^{\mathrm{2}} \right){s}\right)}{{t}} \\ $$$${s}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$${f}'\left({s}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−\left({t}−{t}^{\mathrm{2}} \right)}{{t}\left(\mathrm{1}−\left({t}−{t}^{\mathrm{2}} \right){s}\right)}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}−\mathrm{1}}{\mathrm{1}−\left({t}−{t}^{\mathrm{2}} \right){s}}{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} {s}−{ts}+\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}−\frac{\mathrm{1}}{\mathrm{2}}}{{t}^{\mathrm{2}} {s}−{ts}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}^{\mathrm{2}} {s}−{ts}+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{s}}\left[{ln}\left({t}^{\mathrm{2}} {s}−{ts}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}{s}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{2}} −{t}+\frac{\mathrm{1}}{{s}}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}{s}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{{s}}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$−\frac{\mathrm{2}}{\mathrm{4}−{s}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\left\{\left(\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right).\sqrt{\frac{\mathrm{4}{s}}{\mathrm{4}−{s}}}\right)^{\mathrm{2}} +\mathrm{1}\right\}.} \\ $$$$=−\frac{\mathrm{1}}{\sqrt{{s}\left(\mathrm{4}−{s}\right)}}\left[{arctan}\left(\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)\sqrt{\frac{\mathrm{4}{s}}{\mathrm{4}−{s}}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{2}}{\sqrt{{s}\left(\mathrm{4}−{s}\right)}}\left[{arctg}\left(\sqrt{\frac{{s}}{\mathrm{4}−{s}}}\right)\right] \\ $$$${f}\left({s}\right)=\int−\frac{\mathrm{2}}{\sqrt{{s}\left(\mathrm{4}−{s}\right)}}{arctan}\left(\sqrt{\frac{{s}}{\mathrm{4}−{s}}}\right){ds} \\ $$$${let}\:{u}=\sqrt{\frac{{s}}{\mathrm{4}−{s}}}\Rightarrow{s}=\frac{\mathrm{4}{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} +\mathrm{1}} \\ $$$${ds}=\frac{\mathrm{8}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }{du} \\ $$$${s}\left(\mathrm{4}−{s}\right)=\frac{\mathrm{16}{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int\frac{−\mathrm{2}}{\sqrt{{s}\left(\mathrm{4}−{s}\right)}}\left[{arctan}\left(\sqrt{\frac{\mathrm{4}{s}}{\mathrm{4}−{s}}}\right)\right]{ds} \\ $$$$=\int\frac{−\mathrm{2}}{\sqrt{\frac{\mathrm{16}{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }}}.{arctan}\left({u}\right).\frac{\mathrm{8}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\int\frac{−\mathrm{2}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{4}{u}}{arctan}\left({u}\right).\frac{\mathrm{8}{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{du} \\ $$$$=\int\frac{−\mathrm{4}}{\mathrm{1}+{u}^{\mathrm{2}} }{arctan}\left({u}\right){du} \\ $$$$=−\mathrm{2}\left({arctan}\left({u}\right)\right)^{\mathrm{2}} +{c} \\ $$$$=−\mathrm{2}\left({arctan}\left(\sqrt{\frac{{s}}{\mathrm{4}−{s}}}\right)\right)^{\mathrm{2}} +{c}={f}\left({s}\right) \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}=>{c}=\mathrm{0} \\ $$$${f}\left({s}\right)=−\mathrm{2}\left({arctan}\left(\sqrt{\frac{{s}}{\mathrm{4}−{s}}}\right)\right)^{\mathrm{2}} \\ $$$${k}={f}\left(\mathrm{1}\right)=−\mathrm{2}\left({arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right)^{\mathrm{2}} =−\mathrm{2}\left(\frac{\pi}{\mathrm{6}}\right)^{\mathrm{2}} =\frac{−\pi^{\mathrm{2}} }{\mathrm{18}} \\ $$$$ \\ $$$$ \\ $$
Commented by ~ À ® @ 237 ~ last updated on 05/Sep/19
![Thanks you sir let consider g defined by g(a)=∫_0 ^1 (( ln(1+at+t^2 ))/t)dt , we have D_g =[−2;2] when stating t=(1/u) we get g(a)=∫_1 ^∞ [((−2lnt)/t) + ((ln(1+at+t^2 ))/t) ]dt Now g′(a)= ∫_1 ^∞ (1/t) .(t/(1+at+t^2 )) dt using t^2 +at+1=[(t+(a/2))+((4−a^2 )/4)]=(((4−a^2 )/4))[(((2t+a)/(√(4−a^2 ))))^2 +1] cause a∈D_g So g′(a)=(4/(4−a^2 )) ∫_1 ^∞ (( 1)/(1+(((2t+a)/((√(4−a^2 )) )))^2 )) dt =(2/((√(4−a^2 )) )) [arctan(((2t+a)/((√(4−a^2 )) )))]_1 ^∞ we get g′(a)= ((π−2arctan(((2+a)/(√(4−a^2 )))))/((√(4−a^2 )) )) Now g(a)=∫ (π/((√(4−a^2 )) ))da −2∫ ((arctan((√(((2+a)/(2−a)) )) ))/(√(4−a^2 )))da for the second whole let state u=(√((2+a)/(2−a))) ⇒a=((2(u^2 −1))/(1+u^2 )) and (√(4−a^2 )) =((4u)/(1+u^2 )) , da= ((8udu)/((1+u^2 )^2 )) g(a)= ∫ π((1/2)/(√(1−((a/2))^2 ))) da − 2∫ ((2arctanu)/(1+u^2 )) du then g(a)= πarcsin((a/2)) −2(arctan(√((2+a)/(2−a))) )^2 +c firstly g(−2)=∫_0 ^1 ((ln(1−2t+t^2 ))/t)dt=2∫_0 ^1 ((ln(1−t))/t)dt g(−2)=−2∫_0 ^1 Σ_(n=1) ^∞ (t^(n−1) /n) =−2Σ_(n=1_ ) ^∞ (1/n^2 ) =−(π^2 /3) secondly g(−2)=−(π^2 /2)+c then c=(π^2 /6) Finally we were searching about g(−1)= πarcsin(((−1)/2)) −2(arctan((1/(√3))))^2 +(π^2 /6) g(−1)=((−π^2 )/6) −((2π^2 )/(36)) +(π^2 /6)=−(π^2 /(18))](Q68109.png)
$${Thanks}\:\:{you}\:{sir} \\ $$$${let}\:{consider}\:\:{g}\:{defined}\:{by}\:\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\:\:{ln}\left(\mathrm{1}+{at}+{t}^{\mathrm{2}} \right)}{{t}}{dt}\:\:\:,\:\:{we}\:{have}\:\:{D}_{{g}} =\left[−\mathrm{2};\mathrm{2}\right] \\ $$$${when}\:{stating}\:\:\:{t}=\frac{\mathrm{1}}{{u}}\:\:\:\:\:\:\:{we}\:{get}\:\:\:{g}\left({a}\right)=\int_{\mathrm{1}} ^{\infty} \:\left[\frac{−\mathrm{2}{lnt}}{{t}}\:+\:\frac{{ln}\left(\mathrm{1}+{at}+{t}^{\mathrm{2}} \right)}{{t}}\:\right]{dt} \\ $$$${Now}\:{g}'\left({a}\right)=\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{t}}\:.\frac{{t}}{\mathrm{1}+{at}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${using}\:\:{t}^{\mathrm{2}} +{at}+\mathrm{1}=\left[\left({t}+\frac{{a}}{\mathrm{2}}\right)+\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}\right]=\left(\frac{\mathrm{4}−{a}^{\mathrm{2}} }{\mathrm{4}}\right)\left[\left(\frac{\mathrm{2}{t}+{a}}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right)^{\mathrm{2}} +\mathrm{1}\right]\:\:\:\:\:\:{cause}\:\:{a}\in{D}_{{g}} \: \\ $$$${So}\:\:{g}'\left({a}\right)=\frac{\mathrm{4}}{\mathrm{4}−{a}^{\mathrm{2}} }\:\int_{\mathrm{1}} ^{\infty} \frac{\:\:\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{2}{t}+{a}}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }\:}\right)^{\mathrm{2}} }\:{dt}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }\:}\:\left[{arctan}\left(\frac{\mathrm{2}{t}+{a}}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }\:}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$${we}\:{get}\:\:{g}'\left({a}\right)=\:\frac{\pi−\mathrm{2}{arctan}\left(\frac{\mathrm{2}+{a}}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}\right)}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }\:}\: \\ $$$${Now}\:\:{g}\left({a}\right)=\int\:\frac{\pi}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }\:}{da}\:−\mathrm{2}\int\:\frac{{arctan}\left(\sqrt{\frac{\mathrm{2}+{a}}{\mathrm{2}−{a}}\:}\:\right)}{\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }}{da} \\ $$$${for}\:{the}\:{second}\:{whole}\:{let}\:{state}\:\:\:{u}=\sqrt{\frac{\mathrm{2}+{a}}{\mathrm{2}−{a}}}\:\:\:\Rightarrow{a}=\frac{\mathrm{2}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }\:\:{and}\:\:\sqrt{\mathrm{4}−{a}^{\mathrm{2}} }\:=\frac{\mathrm{4}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\:,\:{da}=\:\frac{\mathrm{8}{udu}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\: \\ $$$${g}\left({a}\right)=\:\int\:\pi\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\sqrt{\mathrm{1}−\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }}\:{da}\:−\:\mathrm{2}\int\:\:\:\frac{\mathrm{2}{arctanu}}{\mathrm{1}+{u}^{\mathrm{2}} }\:{du} \\ $$$$\:\:\:\:{then}\:\:{g}\left({a}\right)=\:\pi{arcsin}\left(\frac{{a}}{\mathrm{2}}\right)\:−\mathrm{2}\left({arctan}\sqrt{\frac{\mathrm{2}+{a}}{\mathrm{2}−{a}}}\:\right)^{\mathrm{2}} +{c} \\ $$$${firstly}\:\:{g}\left(−\mathrm{2}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} \right)}{{t}}{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$${g}\left(−\mathrm{2}\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{{n}−\mathrm{1}} }{{n}}\:=−\mathrm{2}\underset{{n}=\mathrm{1}_{} } {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\: \\ $$$${secondly}\:\:{g}\left(−\mathrm{2}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}+{c} \\ $$$${then}\:{c}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\: \\ $$$${Finally}\:\:{we}\:{were}\:{searching}\:{about} \\ $$$${g}\left(−\mathrm{1}\right)=\:\pi{arcsin}\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\:−\mathrm{2}\left({arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right)^{\mathrm{2}} +\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\: \\ $$$$\:\:{g}\left(−\mathrm{1}\right)=\frac{−\pi^{\mathrm{2}} }{\mathrm{6}}\:−\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{36}}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}\: \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 06/Sep/19
![let f(x) =∫_0 ^1 ((ln(1+xt +t^2 ))/t)dt we must have t^2 +xt +1>0 for all t⇒ x^2 −4<0 ⇒−2<x<2 we have f^′ (x)=∫_0 ^1 (t/(t(1+xt+t^2 )))dt =∫_0 ^1 (dt/(t^2 +xt +1)) =_(t=(1/u)) −∫_1 ^(+∞) ((−du)/(u^2 {(1/u^2 ) +(x/u)+1})) =∫_1 ^(+∞) (du/(1+xu+u^2 )) =∫_1 ^(+∞) (du/(u^2 +2(x/2)u +(x^2 /4)+1−(x^2 /4))) =∫_1 ^(+∞) (du/((u+(x/2))^2 +((4−x^2 )/4))) changement u+(x/2) =((√(4−x^2 ))/2)z givez=((2u+x)/(√(4−x^2 ))) f^′ (x) =(4/(4−x^2 )) ∫_((2+x)/(√(4−x^2 ))) ^(+∞) (1/(1+z^2 ))×((√(4−x^2 ))/2)dz =(2/(√(4−x^2 )))∫_((2+x)/(√(4−x^2 ))) ^(+∞) (dz/(1+z^2 )) =(2/(√(4−x^2 )))[arctanz]_((2+x)/(√(4−x^2 ))) ^(+∞) =(2/(√(4−x^2 ))){(π/2) −arctan(((2+x)/(√(4−x^2 ))))}=(π/(√(4−x^2 )))−(2/(√(4−x^2 ))) arctan(((2+x)/(√(4−x^2 )))) ⇒f(x) =∫ ((πdx)/(√(4−x^2 ))) −2 ∫ (1/(√(4−x^2 ))) arctan(((2+x)/(√(4−x^2 )))) +c changement x =2cosθ give ∫ (1/(√(4−x^2 ))) arctan(((2+x)/(√(4−x^2 )))) =∫ (1/(2sinθ)) arctan(((2+2cosθ)/(2sinθ)))(−2sinθ)cosθ =−∫ arctan(((2cos^2 ((θ/2)))/(2cos((θ/2))sin((θ/2))))) =−∫ arctan((1/(tanθ))) =−((π/2)−θ) =θ−(π/2) =arcos((x/2))−(π/2) ∫ ((πdx)/(√(4−x^2 ))) =_(x =2cosθ) ∫ ((−2πsinθ dθ)/(2sinθ)) =−πθ =−πarccos((x/2)) ⇒ f(x)=−π arcos((x/2))−2 arcos((x/2))+π +c =π−(π+2) arcos((x/2)) +c f(0) =π−(π+2)(π/2) +c =π−(π^2 /2)−π +c =c−(π^2 /2) ⇒c =(π^2 /2)+f(0) =(π^2 /2) +∫_0 ^1 ((ln(1+t^2 ))/t)dt we have ln^, (1+u) =(1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒ ln(1+u) =Σ_(n=0) ^∞ (((−1)^n u^n )/(n+1)) +c(c=0)=Σ_(n=1) ^∞ (−1)^(n−1) (u^n /n) ⇒ ln(1+t^2 ) =Σ_(n=1) ^∞ (((−1)^(n−1) t^(2n) )/n) ⇒((ln(1+t^2 ))/t) =Σ_(n=1) ^∞ (((−1)^(n−1) t^(2n−1) )/n) ⇒∫_0 ^1 ((ln(1+t^2 ))/t)dt =Σ_(n=1) ^∞ (((−1)^n )/n) ∫_0 ^1 t^(2n−1) dt =Σ_(n=1) ^∞ (((−1)^n )/(2n^2 )) =(1/2)Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(1/2)(2^(1−2) −1)ξ(2)=−(1/4)(π^2 /6) =−(π^2 /(24)) ⇒ c =(π^2 /2)−(π^2 /(24)) be continued...](Q68144.png)
$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{xt}\:+{t}^{\mathrm{2}} \right)}{{t}}{dt}\:\:\:\:{we}\:{must}\:{have}\:{t}^{\mathrm{2}} \:+{xt}\:+\mathrm{1}>\mathrm{0}\:{for}\:{all}\:{t}\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{4}<\mathrm{0}\:\Rightarrow−\mathrm{2}<{x}<\mathrm{2}\:\:{we}\:{have}\:{f}^{'} \left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}}{{t}\left(\mathrm{1}+{xt}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{xt}\:+\mathrm{1}}\:=_{{t}=\frac{\mathrm{1}}{{u}}} \:\:\:\:−\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{−{du}}{{u}^{\mathrm{2}} \left\{\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\:+\frac{{x}}{{u}}+\mathrm{1}\right\}} \\ $$$$=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{du}}{\mathrm{1}+{xu}+{u}^{\mathrm{2}} }\:=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}\frac{{x}}{\mathrm{2}}{u}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{du}}{\left({u}+\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{4}−{x}^{\mathrm{2}} }{\mathrm{4}}}\:{changement}\:\:{u}+\frac{{x}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\mathrm{2}}{z}\:{givez}=\frac{\mathrm{2}{u}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{4}}{\mathrm{4}−{x}^{\mathrm{2}} }\:\:\int_{\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}} ^{+\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\mathrm{2}}{dz} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\int_{\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}} ^{+\infty} \:\:\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\left[{arctanz}\right]_{\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}} ^{+\infty} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\left\{\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\right)\right\}=\frac{\pi}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}−\frac{\mathrm{2}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow{f}\left({x}\right)\:=\int\:\frac{\pi{dx}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\:−\mathrm{2}\:\int\:\:\frac{\mathrm{1}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\right)\:+{c} \\ $$$${changement}\:\:{x}\:=\mathrm{2}{cos}\theta\:{give} \\ $$$$\int\:\frac{\mathrm{1}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{2}+{x}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\right)\:=\int\:\frac{\mathrm{1}}{\mathrm{2}{sin}\theta}\:{arctan}\left(\frac{\mathrm{2}+\mathrm{2}{cos}\theta}{\mathrm{2}{sin}\theta}\right)\left(−\mathrm{2}{sin}\theta\right){cos}\theta \\ $$$$=−\int\:\:{arctan}\left(\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2}{cos}\left(\frac{\theta}{\mathrm{2}}\right){sin}\left(\frac{\theta}{\mathrm{2}}\right)}\right)\:=−\int\:\:{arctan}\left(\frac{\mathrm{1}}{{tan}\theta}\right) \\ $$$$=−\left(\frac{\pi}{\mathrm{2}}−\theta\right)\:=\theta−\frac{\pi}{\mathrm{2}}\:={arcos}\left(\frac{{x}}{\mathrm{2}}\right)−\frac{\pi}{\mathrm{2}} \\ $$$$\int\:\frac{\pi{dx}}{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\:=_{{x}\:=\mathrm{2}{cos}\theta} \:\:\:\:\int\:\:\frac{−\mathrm{2}\pi{sin}\theta\:{d}\theta}{\mathrm{2}{sin}\theta}\:=−\pi\theta\:=−\pi{arccos}\left(\frac{{x}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)=−\pi\:{arcos}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}\:{arcos}\left(\frac{{x}}{\mathrm{2}}\right)+\pi\:+{c} \\ $$$$=\pi−\left(\pi+\mathrm{2}\right)\:{arcos}\left(\frac{{x}}{\mathrm{2}}\right)\:+{c} \\ $$$${f}\left(\mathrm{0}\right)\:=\pi−\left(\pi+\mathrm{2}\right)\frac{\pi}{\mathrm{2}}\:+{c}\:=\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\pi\:+{c}\:={c}−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{c}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}+{f}\left(\mathrm{0}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{{t}}{dt} \\ $$$${we}\:{have}\:{ln}^{,} \left(\mathrm{1}+{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{u}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} }{{n}+\mathrm{1}}\:+{c}\left({c}=\mathrm{0}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{{u}^{{n}} }{{n}}\:\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}^{\mathrm{2}{n}} }{{n}}\:\Rightarrow\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{{t}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}^{\mathrm{2}{n}−\mathrm{1}} }{{n}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{{t}}{dt}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{\mathrm{2}{n}−\mathrm{1}} {dt}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{4}}\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\:\Rightarrow \\ $$$${c}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\:\:\:\:{be}\:{continued}... \\ $$