
Question and Answers Forum
Question Number 68270 by ~ À ® @ 237 ~ last updated on 08/Sep/19
![Prove that if Li_2 (x)=Σ_(n=1) (x^n /n^2 ) then ∀ x Li_2 (x)+Li_2 (1−x) = (π^2 /6) −ln(x)ln(1−x) ∀ x∉[0:1] Li_2 (x)+Li_2 ((1/x)) = −(π^2 /6) −[ln(−x)]^2 Find A=Σ_(n=1) ^∞ (ϕ^n /n^2 ) and B=Σ_(n=1) ^∞ (2^n /n^2 )](Q68270.png)
Commented by mathmax by abdo last updated on 10/Sep/19
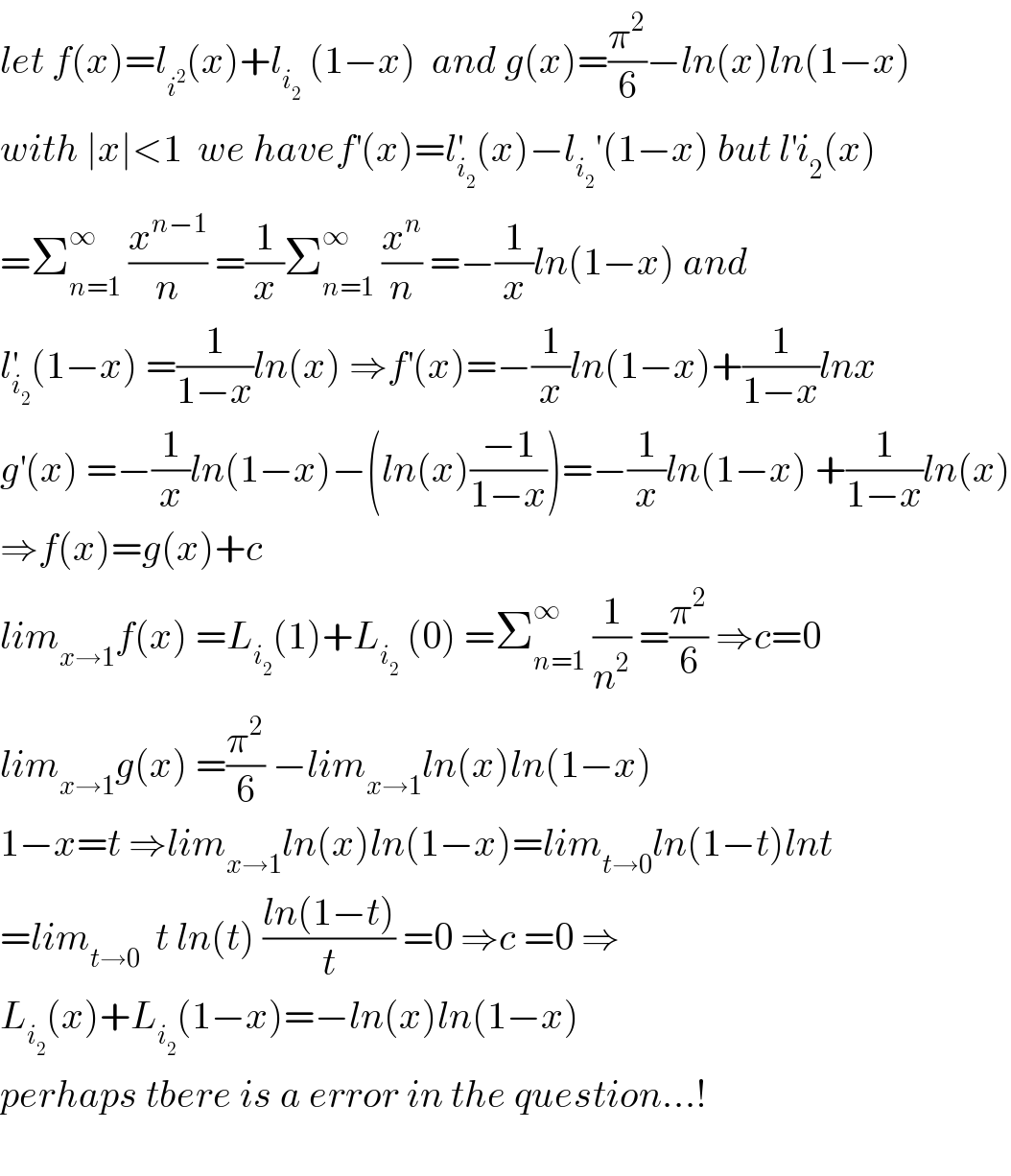
Commented by ~ À ® @ 237 ~ last updated on 10/Sep/19
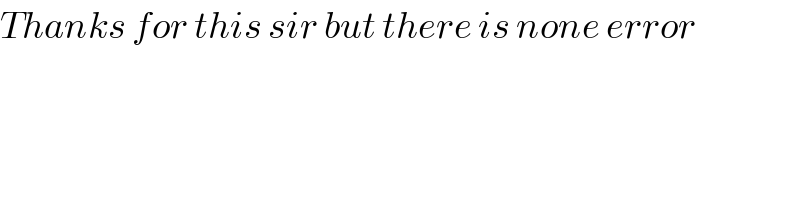
Commented by ~ À ® @ 237 ~ last updated on 10/Sep/19
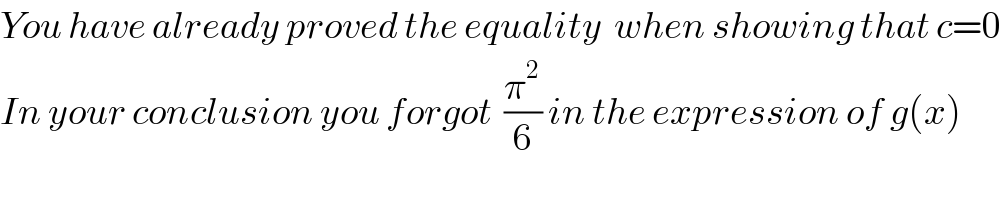
Answered by mind is power last updated on 09/Sep/19
![are you sur for li_2 (x)+li_2 ((1/x))=−(π^2 /6_ )−[ln(−x)]^2 ...](Q68378.png)
Commented by ~ À ® @ 237 ~ last updated on 10/Sep/19
![I forget something here sir: Sorry It is Li_2 (x)+Li_2 ((1/x))=−_ (π^2 /6) −(1/2)[ln(−x)]^2](Q68423.png)
