Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 68309 by ajfour last updated on 08/Sep/19

Commented by ajfour last updated on 08/Sep/19

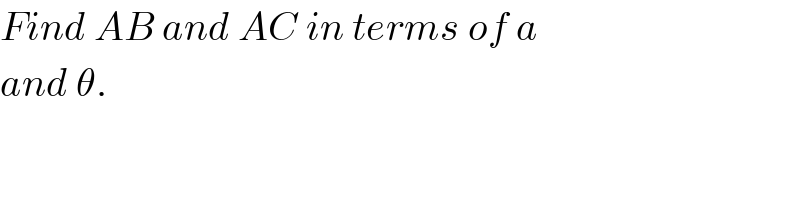
Find AB and AC in terms of a and θ.

$${Find}\:{AB}\:{and}\:{AC}\:{in}\:{terms}\:{of}\:{a}\: \\ $$$${and}\:\theta. \\ $$

Commented by mr W last updated on 08/Sep/19

((AB)/(sin θ))=((AC)/(sin 2θ))=(a/(sin 3θ)) ⇒AB=((a sin θ)/(sin 3θ))=(a/(3−4 sin^2 θ)) ⇒AC=((a sin 2θ)/(sin 3θ))=((2a cos θ)/(3−4 sin^2 θ))

$$\frac{{AB}}{\mathrm{sin}\:\theta}=\frac{{AC}}{\mathrm{sin}\:\mathrm{2}\theta}=\frac{{a}}{\mathrm{sin}\:\mathrm{3}\theta} \\ $$$$\Rightarrow{AB}=\frac{{a}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\mathrm{3}\theta}=\frac{{a}}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{AC}=\frac{{a}\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\mathrm{3}\theta}=\frac{\mathrm{2}{a}\:\mathrm{cos}\:\theta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$

Commented by ajfour last updated on 09/Sep/19

Thank you Sir. I shall find a better question.

$${Thank}\:{you}\:{Sir}.\:{I}\:{shall}\:{find}\:{a} \\ $$$${better}\:{question}. \\ $$

Answered by ajfour last updated on 09/Sep/19

let AC=ap and AB=q ((ap)/(sin 2θ))=(q/(sin θ)) ⇒ q=((ap)/(2cos θ)) cos (π−3θ)=((((p^2 /(4cos^2 θ))+p^2 −1))/((((2p^2 )/(2cos θ))))) ⇒ (3−4cos^2 θ)p^2 =p^2 +(p^2 /(4cos^2 θ))−1 ⇒ (1/p^2 )=(1/(4cos^2 θ))+4cos^2 θ−2 If 0< θ < (π/2) ⇒ (1/p)=(1/(2cos θ))−2cos θ =((1−4cos^2 θ)/(2cos θ)) as AC=ap and AB=((ap)/(2cos θ)) so AC= ((2acos θ)/(1−4cos^2 θ)) ; AB=(a/(1−4cos^2 θ))

$${let}\:\:{AC}={ap}\:\:{and}\:{AB}={q} \\ $$$$\frac{{ap}}{\mathrm{sin}\:\mathrm{2}\theta}=\frac{{q}}{\mathrm{sin}\:\theta}\:\:\Rightarrow\:\:{q}=\frac{{ap}}{\mathrm{2cos}\:\theta} \\ $$$$\mathrm{cos}\:\left(\pi−\mathrm{3}\theta\right)=\frac{\left(\frac{{p}^{\mathrm{2}} }{\mathrm{4cos}\:^{\mathrm{2}} \theta}+{p}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\frac{\mathrm{2}{p}^{\mathrm{2}} }{\mathrm{2cos}\:\theta}\right)} \\ $$$$\Rightarrow\:\left(\mathrm{3}−\mathrm{4cos}\:^{\mathrm{2}} \theta\right){p}^{\mathrm{2}} ={p}^{\mathrm{2}} +\frac{{p}^{\mathrm{2}} }{\mathrm{4cos}\:^{\mathrm{2}} \theta}−\mathrm{1} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4cos}\:^{\mathrm{2}} \theta}+\mathrm{4cos}\:^{\mathrm{2}} \theta−\mathrm{2} \\ $$$$\:\:\:\:{If}\:\:\:\:\mathrm{0}<\:\theta\:<\:\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{p}}=\frac{\mathrm{1}}{\mathrm{2cos}\:\theta}−\mathrm{2cos}\:\theta\:=\frac{\mathrm{1}−\mathrm{4cos}\:^{\mathrm{2}} \theta}{\mathrm{2cos}\:\theta} \\ $$$${as}\:\:{AC}={ap}\:\:{and}\:{AB}=\frac{{ap}}{\mathrm{2cos}\:\theta} \\ $$$${so}\:\:\boldsymbol{{AC}}=\:\frac{\mathrm{2}{a}\mathrm{cos}\:\theta}{\mathrm{1}−\mathrm{4cos}\:^{\mathrm{2}} \theta}\:\:\:;\:\:\boldsymbol{{AB}}=\frac{{a}}{\mathrm{1}−\mathrm{4cos}\:^{\mathrm{2}} \theta}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com