
Question and Answers Forum
Question Number 68342 by Tony Lin last updated on 09/Sep/19

Commented by Tony Lin last updated on 09/Sep/19
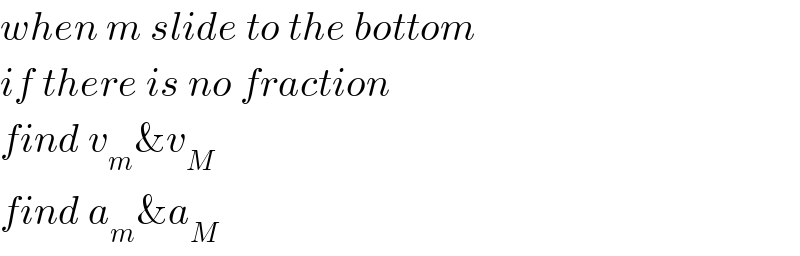
Answered by mr W last updated on 09/Sep/19

Commented by mr W last updated on 10/Sep/19
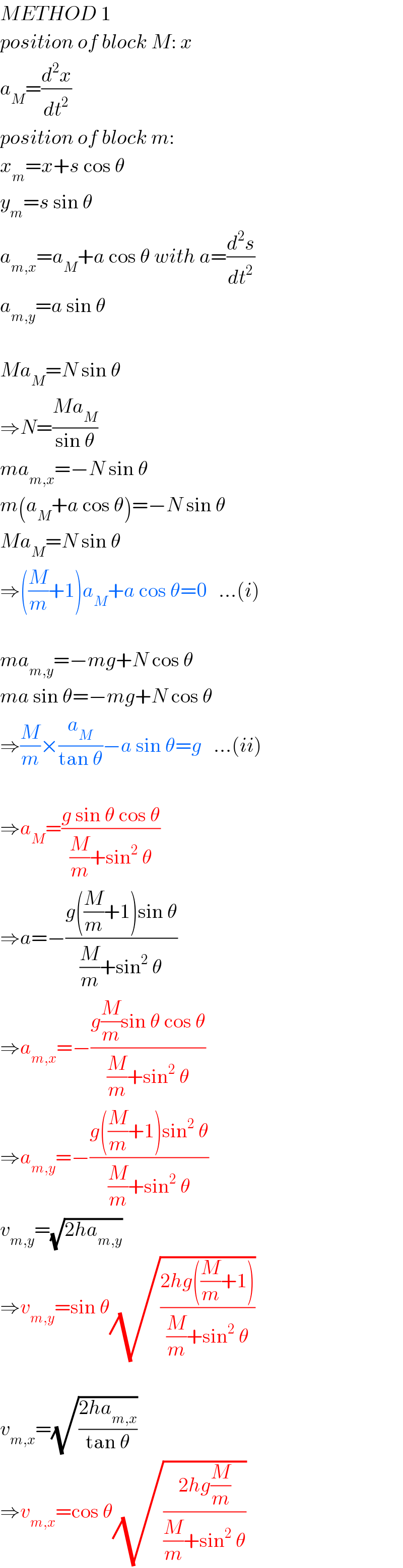
Commented by Tony Lin last updated on 10/Sep/19

Answered by mr W last updated on 09/Sep/19

Commented by mr W last updated on 09/Sep/19

Commented by Tony Lin last updated on 10/Sep/19

Answered by Tanmay chaudhury last updated on 09/Sep/19

Commented by Tanmay chaudhury last updated on 09/Sep/19

Commented by Tony Lin last updated on 10/Sep/19

