Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 68451 by mr W last updated on 10/Sep/19

Commented by mr W last updated on 11/Sep/19

$i f M = 0, t h e b l o c k m j u s t h a s f r e e$ $f a l l, t h e r e f o r e T = \sqrt{2 g h} = \sqrt{2 g R} .$
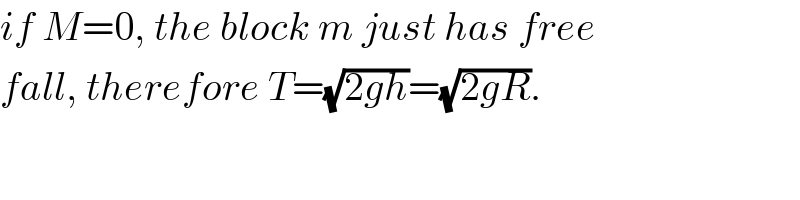
Commented by ajfour last updated on 11/Sep/19

$s o r r y s i r m y m i s t a k e f i r s t,$ $i t m a t c h e d b u t i n t h e e n d i$ $t y p e d i n \sqrt{2 g R} i t i s t i m e n o t$ $v e l o c i t y i t i s \sqrt{\frac{2 R}{g}} (h a . . h a)$ $B y t h e w a y p l e a s e c h e c k, i g o t$ $s o m e a n s w e r f o r f i x e d w e d g e t o o .$
Commented by mr W last updated on 10/Sep/19

$t h e b l o c k m i s r e l e a s e d a t t h e t o p o f$ $t h e w e d g e . t h e r e i s n o f r i c t i o n .$ $f i n d t h e v e l o c i t y o f b o t h o b j e c t s w h e n$ $t h e s m a l l b l o c k r e a c h e s t h e b o t t o m$ $o f t h e w e d g e .$
Commented by ajfour last updated on 11/Sep/19

Commented by ajfour last updated on 11/Sep/19

$L e t s t r y a n d f i n d t i m e i t t a k e s$ $t o s l i p d o w n .$ $N + m A \cos θ - m g \sin θ = \frac{{m v}_{r}^{2}}{R}$ $m A \sin θ + m g \cos θ = \frac{{m v}_{r} {d v}_{r}}{R d θ}$ $N \cos θ = M A$ $\Rightarrow i f w e l e t M = μ m$ $μ A \sec θ + A \cos θ - g \sin θ = \frac{v_{r}^{2}}{R} . . (i)$ $A \sin θ + g \cos θ = \frac{v_{r} {d v}_{r}}{R d θ}$ $\Rightarrow A = (\frac{v_{r} {d v}_{r}}{R d θ} - g \cos θ) cosec θ . . . (i i)$ $\Rightarrow$ $(μ \sec θ + \cos θ) (\frac{v_{r} {d v}_{r}}{R d θ} - g \cos θ) cosec θ$ $- g \sin θ = \frac{v_{r}^{2}}{R}$ $l e t v_{r}^{2} / R = 2 s \Rightarrow v_{r} {d v}_{r} / R = d s$ $N o w$ $(μ \sec θ + \cos θ) (cosec θ) \frac{d s}{d θ} - 2 s$ $= g \sin θ + g \cos θ cosec θ (μ \sec θ + \cos θ)$ $o r$ $\frac{d s}{d θ} - \frac{2 s (\sin θ)}{(μ \sec θ + \cos θ)}$ $= g (\frac{\sin^{2} θ}{μ \sec θ + \cos θ} + \cos θ)$ $\Rightarrow$ $\frac{d s}{\cos θ d θ} - \frac{2 s (\sin θ)}{(μ + \cos^{2} θ)}$ $= g (1 + \frac{\sin^{2} θ}{μ + \cos^{2} θ})$ $l e t \sin θ = u \Rightarrow \cos θ d θ = d u$ $\Rightarrow$ $\frac{d s}{d u} - \frac{2 s u}{μ + 1 - u^{2}} = \frac{g (μ + 1)}{μ + 1 - u^{2}}$ $l e t μ + 1 = λ \Rightarrow$ $\frac{d s}{d u} + \frac{2 s u}{u^{2} - λ} = \frac{λ g}{λ - u^{2}}$ $\Rightarrow (u^{2} - λ) \frac{d s}{d u} + 2 s u = - λ g$ $\Rightarrow \int_{0}^{s (u^{2} - λ)} d [s (u^{2} - λ)] = - λ g \int_{0}^{u} d u$ $\Rightarrow s (u^{2} - λ) = - λ g u$ $\Rightarrow [\frac{v_{r}^{2}}{2 R} (\sin^{2} θ - λ) = - λ g \sin θ]$ $b u t i f w e c o n t i n u e w i t h s a m e$ $v a r i a b l e u = \sin θ, t h e n$ $\Rightarrow v_{r} = \frac{d (R d θ)}{d t} = \sqrt{2 s R} = \sqrt{2 R (\frac{λ g u}{λ - u^{2}})}$ $\int_{0}^{T} d t = \int_{0}^{1} \frac{R d u}{\sqrt{1 - u^{2}}} \sqrt{\frac{λ - u^{2}}{2 λ g R u}}$ $T = \sqrt{\frac{R}{2 λ g}} \int_{0}^{1} \sqrt{\frac{λ - u^{2}}{u (1 - u^{2})}} d u$ $I f w e d g e i s f a r t o o h e a v i e r, t h e n$ $i t i s a s g o o d a s f i x e d;$ $μ = \frac{M}{m} \to \infty$ $T = \sqrt{\frac{R}{2 g}} \int_{0}^{1} \frac{d u}{\sqrt{u (1 - u^{2})}}$ $= t_{0} \int_{0}^{π / 2} \frac{\cos θ d θ}{\sqrt{\sin θ \cos^{2} θ}}$ $= t_{0} \int_{0}^{π / 2} \frac{d θ}{\sqrt{\sin θ}} l e t \sin θ = t^{2}$ $\Rightarrow 2 t d t = \cos θ d θ$ $\Rightarrow d θ = \frac{2 t d t}{\sqrt{1 - t^{2}}}$ $T = t_{0} \int_{0}^{1} \frac{2 t d t}{t \sqrt{1 - t^{2}}} = 2 t_{0} \int_{0}^{1} \frac{d t}{\sqrt{1 - t^{2}}}$ $= 2 t_{0} (\frac{π}{2}) = π t_{0}$ $T = π \sqrt{\frac{R}{2 g}}!$ $I f t h e r e i s a v e r y l i g h t w e d g e$ $(j u s t t o c h e c k)$ $μ = \frac{M}{m} \to 0 \Rightarrow λ \to 1$ $T = \sqrt{\frac{R}{2 g}} \int_{0}^{1} \frac{d u}{\sqrt{u}}$ $T = \sqrt{\frac{2 R}{g}} (f a b u l o u s!)$ $b u t i t h i n k o t h e r w i s e s o l v i n g t h e$ $i n t e g r a t i o n i s b e y o n d m y$ $u n d e r s t a n d i n g . .$
Commented by mr W last updated on 11/Sep/19

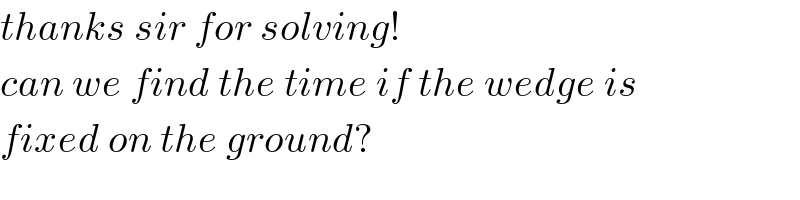
$t h a n k s s i r f o r s o l v i n g!$ $c a n w e f i n d t h e t i m e i f t h e w e d g e i s$ $f i x e d o n t h e g r o u n d ?$
Commented by mr W last updated on 11/Sep/19

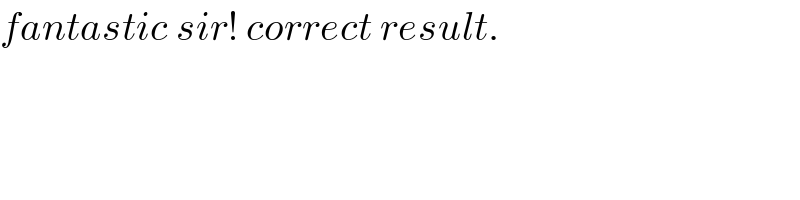
$f a n t a s t i c s i r! c o r r e c t r e s u l t .$
	Answered by ajfour last updated on 10/Sep/19

	$m g R = \frac{1}{2} {m v}^{2} + \frac{1}{2} {M V}^{2}$ $m v = M V$ $2 m g R = [m + M {(\frac{m}{M})}^{2}] v^{2}$ $v = \sqrt{\frac{2 M g R}{M + m}}, V = \sqrt{\frac{2 m g R}{M + m}} .$
	Commented by mr W last updated on 11/Sep/19

	$s i m p l e a n d d i r e c t, g r e a t!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum