
Previous in Relation and Functions Next in Relation and Functions
Question Number 68466 by mathmax by abdo last updated on 11/Sep/19

$${let}\:{f}\left({x}\right)\:=\int_{{x}^{} } ^{{x}^{\mathrm{2}} −{x}} \:{arctan}\left({e}^{−{x}−{t}} \right){dt} \\ $$$${calculate}\:{f}^{'} \left({x}\right)\:\:\:{and}\:{f}^{'} \left(\mathrm{0}\right). \\ $$
Commented by mathmax by abdo last updated on 11/Sep/19
![we have g(x,t)=arctan(e^(−x−t) ) ,u(x)=x and v(x)=x^2 −x ⇒ f^′ (x) =∫_(u(x)) ^(v(x)) (∂g/∂x)(x,t)dt +v^′ g(x,v)−u^′ g(x,u) =∫_x ^(x^2 −x) ((−e^(−x−t) )/(1+e^(−2x−2t) ))dt +(2x−1)g(x,x^2 −x)−g(x,x) =−e^(−x) ∫_x ^(x^2 −x) (e^(−t) /(1+e^(−2t−2x) ))dt +(2x−1)arctan(e^(−x^2 ) ) −arctan(e^(−2x) ) let find I =∫_x ^(x^2 −x) (e^(−t) /(1+e^(−2t−2x) ))dt ⇒ I =∫_x ^(x^2 −1) (e^t /(e^(2t) +e^(−2x) )) dt =_(e^t =u) ∫_e^x ^e^(x^2 −x) (u/(u^2 +e^(−2x) )) (du/u) =∫_e^x ^e^(x^2 −x) (du/(u^2 +e^(−2x) )) =_(u=e^(−x) z) ∫_e^(2x) ^e^x^2 ((e^(−x) dz)/(e^(−2x) (z^2 +1))) =e^x [arctanz]_e^(2x) ^e^x^2 =e^x { arctan(e^x^2 )−arctan(e^(2x) )} ⇒ f^′ (x) =−arctan(e^x^2 )+e^(−x) arctan(e^(2x) )+(2x−1)arctan(e^(−x^2 ) ) −arctan(e^(−2x) ) .](Q68478.png)
$${we}\:{have}\:{g}\left({x},{t}\right)={arctan}\left({e}^{−{x}−{t}} \right)\:\:\:,{u}\left({x}\right)={x}\:{and}\:{v}\left({x}\right)={x}^{\mathrm{2}} −{x}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\int_{{u}\left({x}\right)} ^{{v}\left({x}\right)} \frac{\partial{g}}{\partial{x}}\left({x},{t}\right){dt}\:+{v}^{'} {g}\left({x},{v}\right)−{u}^{'} {g}\left({x},{u}\right) \\ $$$$=\int_{{x}} ^{{x}^{\mathrm{2}} −{x}} \:\:\frac{−{e}^{−{x}−{t}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}−\mathrm{2}{t}} }{dt}\:\:+\left(\mathrm{2}{x}−\mathrm{1}\right){g}\left({x},{x}^{\mathrm{2}} −{x}\right)−{g}\left({x},{x}\right) \\ $$$$=−{e}^{−{x}} \:\int_{{x}} ^{{x}^{\mathrm{2}} −{x}} \:\:\frac{{e}^{−{t}} }{\mathrm{1}+{e}^{−\mathrm{2}{t}−\mathrm{2}{x}} }{dt}\:\:+\left(\mathrm{2}{x}−\mathrm{1}\right){arctan}\left({e}^{−{x}^{\mathrm{2}} } \right) \\ $$$$−{arctan}\left({e}^{−\mathrm{2}{x}} \right)\:\:{let}\:{find}\:{I}\:=\int_{{x}} ^{{x}^{\mathrm{2}} −{x}} \:\frac{{e}^{−{t}} }{\mathrm{1}+{e}^{−\mathrm{2}{t}−\mathrm{2}{x}} }{dt}\:\Rightarrow \\ $$$${I}\:=\int_{{x}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \:\:\frac{{e}^{{t}} }{{e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{x}} }\:{dt}\:\:\:=_{{e}^{{t}} ={u}} \:\:\:\:\:\int_{{e}^{{x}} } ^{{e}^{{x}^{\mathrm{2}} −{x}} } \:\:\:\:\frac{{u}}{{u}^{\mathrm{2}} \:+{e}^{−\mathrm{2}{x}} }\:\frac{{du}}{{u}} \\ $$$$=\int_{{e}^{{x}} } ^{{e}^{{x}^{\mathrm{2}} −{x}} } \:\:\frac{{du}}{{u}^{\mathrm{2}} \:+{e}^{−\mathrm{2}{x}} }\:=_{{u}={e}^{−{x}} \:{z}} \:\:\:\:\int_{{e}^{\mathrm{2}{x}} } ^{{e}^{{x}^{\mathrm{2}} } } \:\:\:\:\frac{{e}^{−{x}} {dz}}{{e}^{−\mathrm{2}{x}} \left({z}^{\mathrm{2}} +\mathrm{1}\right)}\:={e}^{{x}} \left[{arctanz}\right]_{{e}^{\mathrm{2}{x}} } ^{{e}^{{x}^{\mathrm{2}} } } \\ $$$$={e}^{{x}} \left\{\:{arctan}\left({e}^{{x}^{\mathrm{2}} } \right)−{arctan}\left({e}^{\mathrm{2}{x}} \right)\right\}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=−{arctan}\left({e}^{{x}^{\mathrm{2}} } \right)+{e}^{−{x}} \:{arctan}\left({e}^{\mathrm{2}{x}} \right)+\left(\mathrm{2}{x}−\mathrm{1}\right){arctan}\left({e}^{−{x}^{\mathrm{2}} } \right) \\ $$$$−{arctan}\left({e}^{−\mathrm{2}{x}} \right)\:. \\ $$
Commented by mathmax by abdo last updated on 11/Sep/19

$${f}^{'} \left(\mathrm{0}\right)\:=−\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{4}}\:\Rightarrow{f}^{'} \left(\mathrm{0}\right)\:=−\frac{\pi}{\mathrm{2}} \\ $$
Answered by meme last updated on 11/Sep/19

$${f}^{'} \left({x}\right)={arctan}\left({e}^{−{x}−{x}^{\mathrm{2}} +{x}} \right)−{arctan}\left({e}^{−{x}−{x}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{arctan}\left({e}^{−{x}^{\mathrm{2}} } \right)−{arctan}\left({e}^{−\mathrm{2}{x}} \right) \\ $$$$\:\:\:\:{f}^{'} \left(\mathrm{0}\right)={arctan}\left(\mathrm{1}\right)−{arctan}\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{0} \\ $$
Commented by turbo msup by abdo last updated on 11/Sep/19
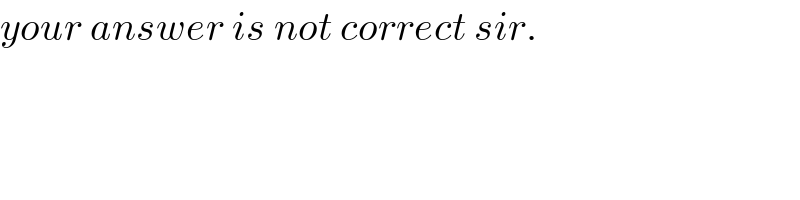
$${your}\:{answer}\:{is}\:{not}\:{correct}\:{sir}. \\ $$
