Question Number 68487 by mr W last updated on 11/Sep/19
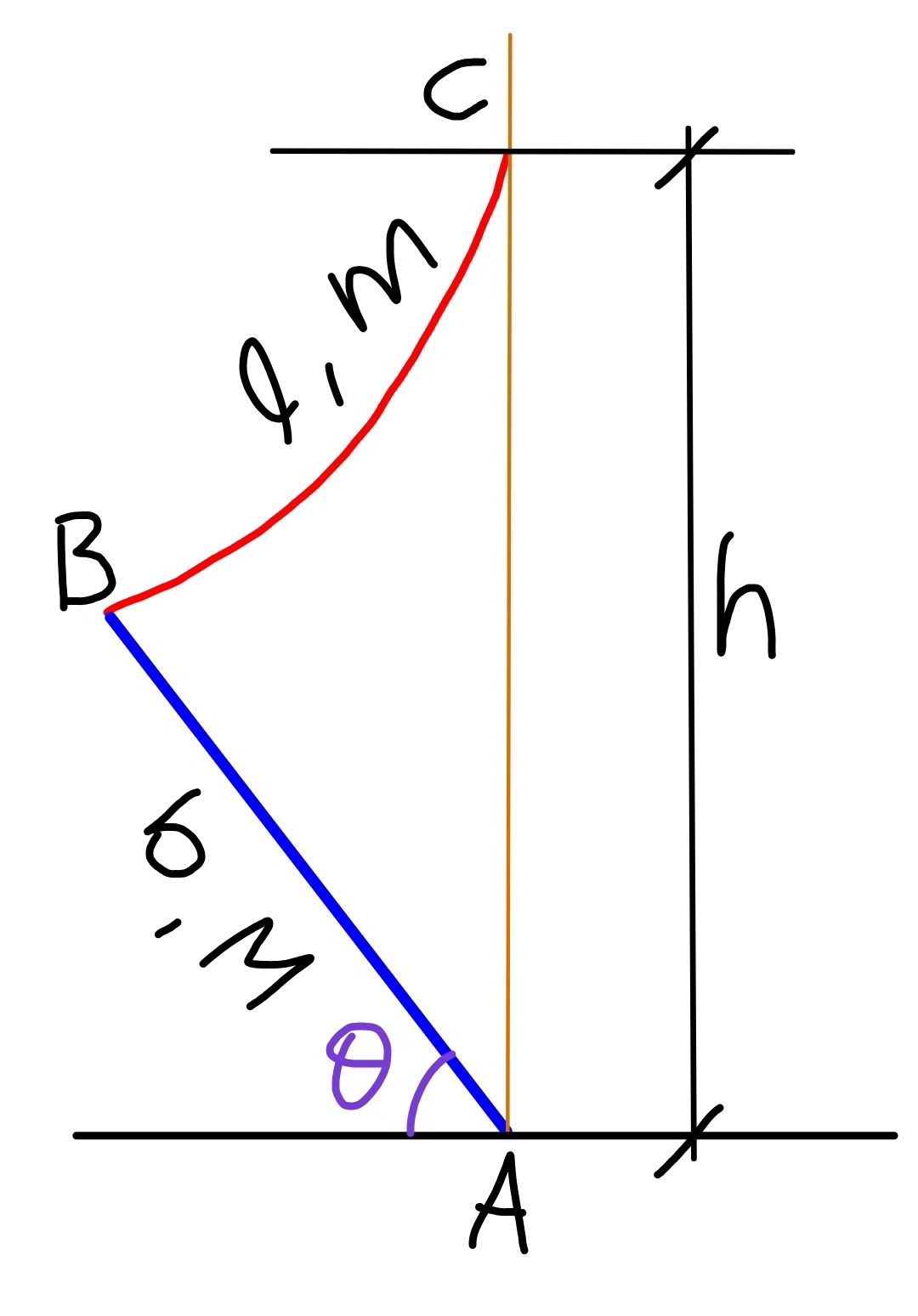
Commented by mr W last updated on 11/Sep/19
$${rod}\:{AB}\:{has}\:{length}\:{b}\:{and}\:{mass}\:{M}, \\ $$$${rope}\:{BC}\:{has}\:{length}\:{l}\:{and}\:{mass}\:{m}, \\ $$$${the}\:{friction}\:{between}\:{rod}\:{and}\:{ground} \\ $$$${is}\:{sufficient},\:{such}\:{that}\:{point}\:{A}\:{can} \\ $$$${not}\:{slide}. \\ $$$${l}+{b}>{h} \\ $$$${find}\:\theta=? \\ $$
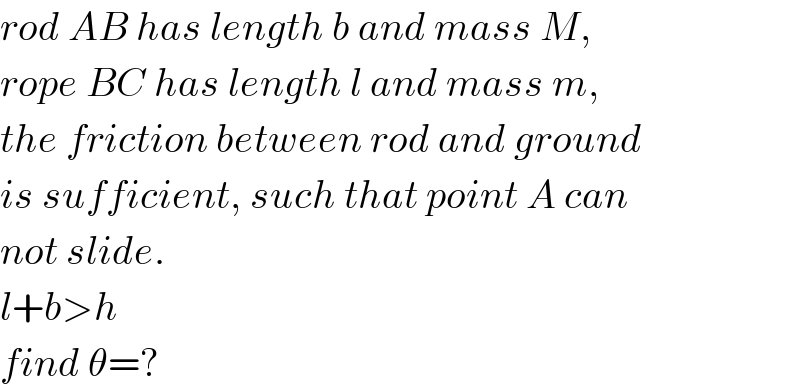
Commented by mr W last updated on 13/Sep/19
$${ajfour}\:{sir}: \\ $$$${can}\:{you}\:{try}\:{to}\:{get}\:{a}\:{single}\:{equation} \\ $$$${to}\:{determine}\:\theta? \\ $$
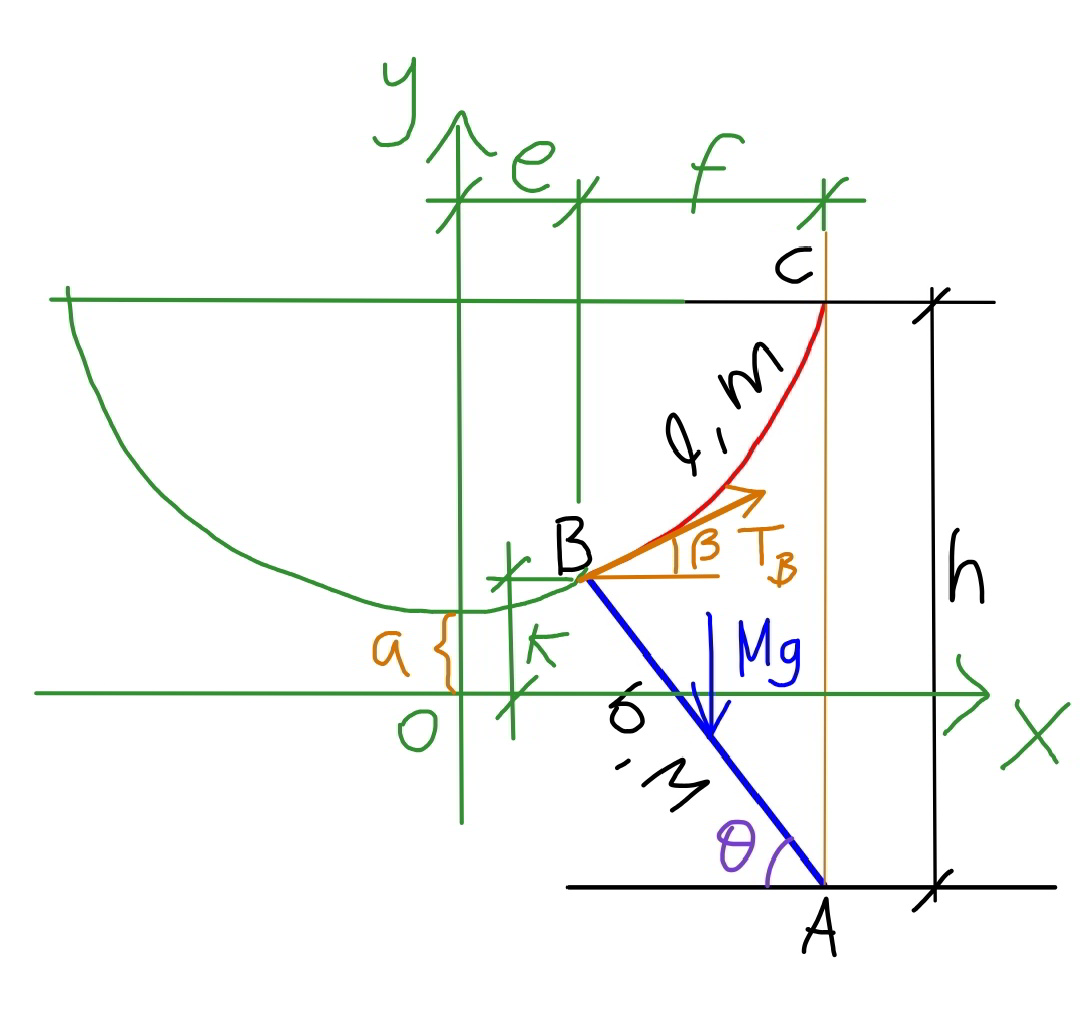
Answered by mr W last updated on 12/Sep/19
Commented by Prithwish sen last updated on 13/Sep/19
$$\mathrm{excellent}\:\mathrm{sir}\:! \\ $$
Commented by mr W last updated on 13/Sep/19
![mass of rope of unit length ρ=(m/l) T_0 =horizontal component of tension in rope let a=(T_0 /(ρg)) the rope BC is a part of a catenary with equation y=a cosh (x/a) in coordinate system as shown in the diagram above. T_B cos β=T_0 =aρg T_B b sin (θ+β)=((Mgb cos θ)/2) ((aρg)/(cos β))sin (θ+β)=((Mg cos θ)/2) ((am)/(l cos β))sin (θ+β)=((M cos θ)/2) ((a(sin θ cos β+cos θ sin β))/(cos β cos θ))=((Ml)/(2m)) ⇒tan θ+tan β=((μl)/a) with μ=(M/(2m)) at point B: k=a cosh (e/a) y′=tan β=sinh (e/a) at point C: f=b cos θ k+h−b sin θ=a cosh ((e+f)/a) a cosh (e/a)+h−b sin θ=a cosh ((e+f)/a) ⇒h−b sin θ=a(cosh ((e+f)/a)−cosh (e/a)) l=a(sinh ((e+f)/a)−sinh (e/a)) ⇒sinh ((e+f)/a)−sinh (e/a)=(l/a) ⇒tan θ+sinh (e/a)=((μl)/a) ⇒(e/a)=sinh^(−1) (((μl)/a)−tan θ) ⇒sinh ((e+f)/a)=((l(1+μ))/a)−tan θ ⇒((e+f)/a)=sinh^(−1) [((l(1+μ))/a)−tan θ] ⇒(e/a)+(f/a)=sinh^(−1) [((l(1+μ))/a)−tan θ] ⇒sinh^(−1) (((μl)/a)−tan θ)+((b cos θ)/a)=sinh^(−1) [((l(1+μ))/a)−tan θ] ⇒sinh^(−1) [((l(1+μ))/a)−tan θ]−sinh^(−1) (((μl)/a)−tan θ)=(l/a)×((b cos θ)/l) ⇒cosh {sinh^(−1) [((l(1+μ))/a)−tan θ]}−cosh {sinh^(−1) (((μl)/a)−tan θ)}=(l/a)×((h−b sin θ)/l) let λ=(l/a) ⇒sinh^(−1) [(1+μ)λ−tan θ]−sinh^(−1) (μλ−tan θ)=((λb cos θ)/l) ...(i) ⇒cosh {sinh^(−1) [(1+μ)λ−tan θ]}−cosh {sinh^(−1) (μλ−tan θ)}=((λ(h−b sin θ))/l) ...(ii) unknowns in (i) and (ii): λ and θ example: μ=(M/(2m))=2 l=2 b=3 h=4 ⇒θ=61.617° (θ=61.045° if rope were massless)](Q68520.png)
$${mass}\:{of}\:{rope}\:{of}\:{unit}\:{length}\:\rho=\frac{{m}}{{l}} \\ $$$${T}_{\mathrm{0}} ={horizontal}\:{component}\:{of}\:{tension} \\ $$$${in}\:{rope} \\ $$$${let}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}} \\ $$$${the}\:{rope}\:{BC}\:{is}\:{a}\:{part}\:{of}\:{a}\:{catenary} \\ $$$${with}\:{equation} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}}\:{in}\:{coordinate}\:{system} \\ $$$${as}\:{shown}\:{in}\:{the}\:{diagram}\:{above}. \\ $$$${T}_{{B}} \:\mathrm{cos}\:\beta={T}_{\mathrm{0}} ={a}\rho{g} \\ $$$${T}_{{B}} {b}\:\mathrm{sin}\:\left(\theta+\beta\right)=\frac{{Mgb}\:\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\frac{{a}\rho{g}}{\mathrm{cos}\:\beta}\mathrm{sin}\:\left(\theta+\beta\right)=\frac{{Mg}\:\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\frac{{am}}{{l}\:\mathrm{cos}\:\beta}\mathrm{sin}\:\left(\theta+\beta\right)=\frac{{M}\:\mathrm{cos}\:\theta}{\mathrm{2}} \\ $$$$\frac{{a}\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\beta+\mathrm{cos}\:\theta\:\mathrm{sin}\:\beta\right)}{\mathrm{cos}\:\beta\:\mathrm{cos}\:\theta}=\frac{{Ml}}{\mathrm{2}{m}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta+\mathrm{tan}\:\beta=\frac{\mu{l}}{{a}}\:{with}\:\mu=\frac{{M}}{\mathrm{2}{m}} \\ $$$${at}\:{point}\:{B}: \\ $$$${k}={a}\:\mathrm{cosh}\:\frac{{e}}{{a}} \\ $$$${y}'=\mathrm{tan}\:\beta=\mathrm{sinh}\:\frac{{e}}{{a}} \\ $$$${at}\:{point}\:{C}: \\ $$$${f}={b}\:\mathrm{cos}\:\theta \\ $$$${k}+{h}−{b}\:\mathrm{sin}\:\theta={a}\:\mathrm{cosh}\:\frac{{e}+{f}}{{a}} \\ $$$${a}\:\mathrm{cosh}\:\frac{{e}}{{a}}+{h}−{b}\:\mathrm{sin}\:\theta={a}\:\mathrm{cosh}\:\frac{{e}+{f}}{{a}} \\ $$$$\Rightarrow{h}−{b}\:\mathrm{sin}\:\theta={a}\left(\mathrm{cosh}\:\frac{{e}+{f}}{{a}}−\mathrm{cosh}\:\frac{{e}}{{a}}\right) \\ $$$${l}={a}\left(\mathrm{sinh}\:\frac{{e}+{f}}{{a}}−\mathrm{sinh}\:\frac{{e}}{{a}}\right) \\ $$$$\Rightarrow\mathrm{sinh}\:\frac{{e}+{f}}{{a}}−\mathrm{sinh}\:\frac{{e}}{{a}}=\frac{{l}}{{a}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta+\mathrm{sinh}\:\frac{{e}}{{a}}=\frac{\mu{l}}{{a}} \\ $$$$\Rightarrow\frac{{e}}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\mu{l}}{{a}}−\mathrm{tan}\:\theta\right) \\ $$$$\Rightarrow\mathrm{sinh}\:\frac{{e}+{f}}{{a}}=\frac{{l}\left(\mathrm{1}+\mu\right)}{{a}}−\mathrm{tan}\:\theta \\ $$$$\Rightarrow\frac{{e}+{f}}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left[\frac{{l}\left(\mathrm{1}+\mu\right)}{{a}}−\mathrm{tan}\:\theta\right] \\ $$$$\Rightarrow\frac{{e}}{{a}}+\frac{{f}}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left[\frac{{l}\left(\mathrm{1}+\mu\right)}{{a}}−\mathrm{tan}\:\theta\right] \\ $$$$\Rightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\mu{l}}{{a}}−\mathrm{tan}\:\theta\right)+\frac{{b}\:\mathrm{cos}\:\theta}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left[\frac{{l}\left(\mathrm{1}+\mu\right)}{{a}}−\mathrm{tan}\:\theta\right] \\ $$$$\Rightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left[\frac{{l}\left(\mathrm{1}+\mu\right)}{{a}}−\mathrm{tan}\:\theta\right]−\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\mu{l}}{{a}}−\mathrm{tan}\:\theta\right)=\frac{{l}}{{a}}×\frac{{b}\:\mathrm{cos}\:\theta}{{l}} \\ $$$$\Rightarrow\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left[\frac{{l}\left(\mathrm{1}+\mu\right)}{{a}}−\mathrm{tan}\:\theta\right]\right\}−\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\mu{l}}{{a}}−\mathrm{tan}\:\theta\right)\right\}=\frac{{l}}{{a}}×\frac{{h}−{b}\:\mathrm{sin}\:\theta}{{l}} \\ $$$${let}\:\lambda=\frac{{l}}{{a}} \\ $$$$\Rightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left[\left(\mathrm{1}+\mu\right)\lambda−\mathrm{tan}\:\theta\right]−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mu\lambda−\mathrm{tan}\:\theta\right)=\frac{\lambda{b}\:\mathrm{cos}\:\theta}{{l}}\:\:\:\:\:\:\:...\left({i}\right) \\ $$$$\Rightarrow\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left[\left(\mathrm{1}+\mu\right)\lambda−\mathrm{tan}\:\theta\right]\right\}−\mathrm{cosh}\:\left\{\mathrm{sinh}^{−\mathrm{1}} \:\left(\mu\lambda−\mathrm{tan}\:\theta\right)\right\}=\frac{\lambda\left({h}−{b}\:\mathrm{sin}\:\theta\right)}{{l}}\:\:\:\:\:\:...\left({ii}\right) \\ $$$${unknowns}\:{in}\:\left({i}\right)\:{and}\:\left({ii}\right):\:\lambda\:{and}\:\theta \\ $$$$ \\ $$$${example}: \\ $$$$\mu=\frac{{M}}{\mathrm{2}{m}}=\mathrm{2} \\ $$$${l}=\mathrm{2} \\ $$$${b}=\mathrm{3} \\ $$$${h}=\mathrm{4} \\ $$$$\Rightarrow\theta=\mathrm{61}.\mathrm{617}° \\ $$$$\left(\theta=\mathrm{61}.\mathrm{045}°\:{if}\:{rope}\:{were}\:{massless}\right) \\ $$
Commented by Prithwish sen last updated on 13/Sep/19
$$\mathrm{but}\:\mathrm{what}\:\mathrm{if}\:\mathrm{BC}\:\mathrm{is}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}. \\ $$
Commented by mr W last updated on 13/Sep/19
$${if}\:{BC}\:{is}\:{straight}\:{line},\:{i}.{e}.\:{the}\:{rope}\:{is} \\ $$$${massless},\:{then}\:{it}\:{is}\:{a}\:{pure}\:{geometric} \\ $$$${question}\:{for}\:{a}\:{triangle}\:{with}\:{sides} \\ $$$${b},\:{l}\:{and}\:{h}. \\ $$$$\mathrm{sin}\:\theta=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\frac{{b}^{\mathrm{2}} +{h}^{\mathrm{2}} −{l}^{\mathrm{2}} }{\mathrm{2}{bh}} \\ $$$$\Rightarrow\theta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{b}^{\mathrm{2}} +{h}^{\mathrm{2}} −{l}^{\mathrm{2}} }{\mathrm{2}{bh}}\right) \\ $$
Commented by Prithwish sen last updated on 13/Sep/19
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$