
Question Number 68624 by TawaTawa last updated on 14/Sep/19

Answered by Rasheed.Sindhi last updated on 14/Sep/19
![A Tricky Approach k=−3((1/(a^2 −a+1))+(1/(b^2 −b+1)))+c =−3(((a+1)/((a+1)(a^2 −a+1)))+((b+1)/((b+1)(b^2 −b+1))))+c =−3(((a+1)/(a^3 +1))+((b+1)/(b^3 +1)))+c =−3(((a+1)/(a^3 +4−3))+((b+1)/(b^3 +4−3)))+c =−3(((a+1)/(−3))+((b+1)/(−3)))+c =a+b+c+2 =0+2=2 [a,b,c are cuberoots and their sum should be 0] Hence k=2](Q68633.png)
$$\mathbb{A}\:\mathbb{T}\boldsymbol{\mathrm{ricky}}\:\mathbb{A}\boldsymbol{\mathrm{pproach}} \\ $$$$\mathrm{k}=−\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} −\mathrm{a}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} −\mathrm{b}+\mathrm{1}}\right)+\mathrm{c} \\ $$$$\:\:=−\mathrm{3}\left(\frac{\mathrm{a}+\mathrm{1}}{\left(\mathrm{a}+\mathrm{1}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{a}+\mathrm{1}\right)}+\frac{\mathrm{b}+\mathrm{1}}{\left(\mathrm{b}+\mathrm{1}\right)\left(\mathrm{b}^{\mathrm{2}} −\mathrm{b}+\mathrm{1}\right)}\right)+\mathrm{c} \\ $$$$\:\:=−\mathrm{3}\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}^{\mathrm{3}} +\mathrm{1}}+\frac{\mathrm{b}+\mathrm{1}}{\mathrm{b}^{\mathrm{3}} +\mathrm{1}}\right)+\mathrm{c} \\ $$$$\:\:=−\mathrm{3}\left(\frac{\mathrm{a}+\mathrm{1}}{\mathrm{a}^{\mathrm{3}} +\mathrm{4}−\mathrm{3}}+\frac{\mathrm{b}+\mathrm{1}}{\mathrm{b}^{\mathrm{3}} +\mathrm{4}−\mathrm{3}}\right)+\mathrm{c} \\ $$$$\:\:=−\mathrm{3}\left(\frac{\mathrm{a}+\mathrm{1}}{−\mathrm{3}}+\frac{\mathrm{b}+\mathrm{1}}{−\mathrm{3}}\right)+\mathrm{c} \\ $$$$\:\:\:=\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{2} \\ $$$$\:\:\:=\mathrm{0}+\mathrm{2}=\mathrm{2} \\ $$$$\:\left[\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{are}\:\mathrm{cuberoots}\:\mathrm{and}\:\mathrm{their}\:\mathrm{sum}\:\mathrm{should}\:\mathrm{be}\:\mathrm{0}\right] \\ $$$$\mathrm{Hence}\:\mathrm{k}=\mathrm{2} \\ $$
Commented by TawaTawa last updated on 17/Sep/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 14/Sep/19
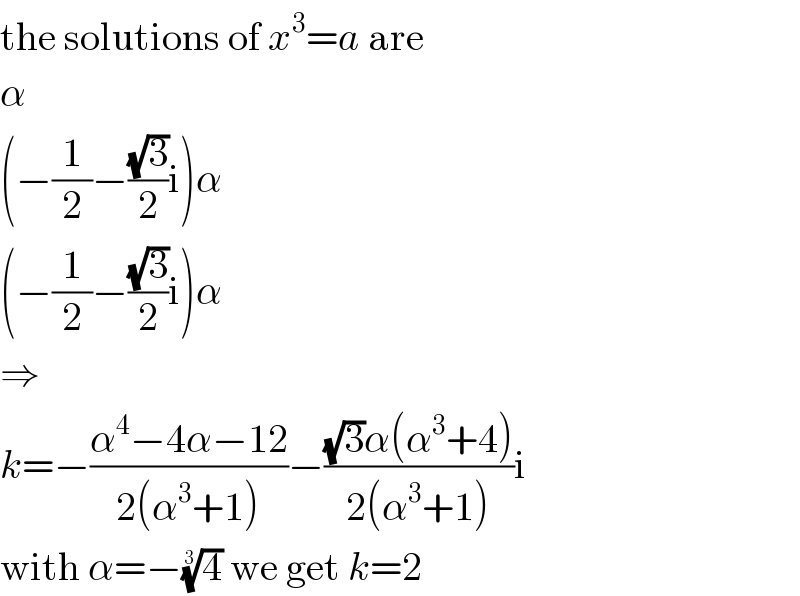
$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:{x}^{\mathrm{3}} ={a}\:\mathrm{are} \\ $$$$\alpha \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\alpha \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\alpha \\ $$$$\Rightarrow \\ $$$${k}=−\frac{\alpha^{\mathrm{4}} −\mathrm{4}\alpha−\mathrm{12}}{\mathrm{2}\left(\alpha^{\mathrm{3}} +\mathrm{1}\right)}−\frac{\sqrt{\mathrm{3}}\alpha\left(\alpha^{\mathrm{3}} +\mathrm{4}\right)}{\mathrm{2}\left(\alpha^{\mathrm{3}} +\mathrm{1}\right)}\mathrm{i} \\ $$$$\mathrm{with}\:\alpha=−\sqrt[{\mathrm{3}}]{\mathrm{4}}\:\mathrm{we}\:\mathrm{get}\:{k}=\mathrm{2} \\ $$
Commented by TawaTawa last updated on 14/Sep/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
