Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 6865 by Tawakalitu. last updated on 31/Jul/16

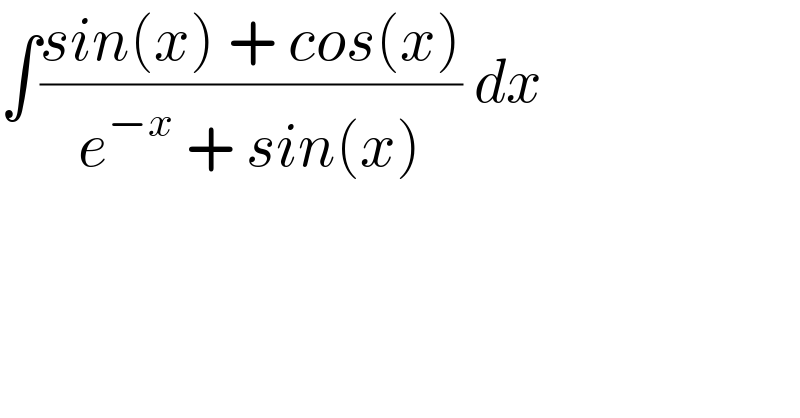
∫((sin(x) + cos(x))/(e^(−x) + sin(x))) dx

$$\int\frac{{sin}\left({x}\right)\:+\:{cos}\left({x}\right)}{{e}^{−{x}} \:+\:{sin}\left({x}\right)}\:{dx} \\ $$

Commented by Yozzii last updated on 31/Jul/16

sinhix=isinx sinx=((sinhix)/i)=((e^(ix) −e^(−ix) )/(2i)) cosx=coshix=((e^(ix) +e^(−ix) )/2) sinx+cosx=((e^(ix) −e^(−ix) +ie^(ix) +ie^(−ix) )/(2i))=((e^(ix) (1+i)+e^(−ix) (i−1))/(2i)) e^(−x) +sinx=((2ie^(−x) +e^(ix) −e^(−ix) )/(2i)) I=∫((sinx+cosx)/(e^(−x) +sinx))dx=∫((e^(ix) (i+1)+e^(−ix) (i−1))/(e^(ix) −e^(−ix) +2ie^(−x) ))dx I=∫(e^x /e^x )×((e^(ix) (i+1)+e^(−ix) (i−1))/(e^(ix) −e^(−ix) +2ie^(−x) ))dx=∫((e^(x(i+1)) (i+1)−e^(x(1−i)) (1−i))/(e^(x(i+1)) −e^(x(1−i)) +2i))dx Let u=e^(x(1+i)) −e^(x(1−i)) +2i. ⇒du={e^(x(1+i)) (i+1)−e^(x(1−i)) (1−i)}dx ⇒I=∫(du/u)=ln∣u∣+C I=ln∣e^(x(1+i)) −e^(x(1−i)) +2i∣+C u=e^x (e^(ix) −e^(−ix) )+2i u=e^x (2isinx)+2i u=2i(e^x sinx+1) ∴ I=ln∣2i(e^x sinx+1)∣+C I=ln2+ln∣e^x sinx+1∣+C ∫((sinx+cosx)/(e^(−x) +sinx))dx=ln∣e^x sinx+1∣+D D=constant Checking: (d/dx)ln(e^x sinx+1)=((e^x (cosx+sinx))/(e^x sinx+1))=((sinx+cosx)/(sinx+e^(−x) )) −−−−−−−−−−−−−−−−−−−−−−−− This answer suggests the folliwing approach: I=∫((sinx+cosx)/(e^(−x) +sinx))dx=∫((e^x (sinx+cosx))/(1+e^x sinx))dx. Let u=1+e^x sinx⇒du=e^x (cosx+sinx)dx I=∫(du/u)=ln∣u∣=ln∣e^x sinx+1∣+C.

$${sinhix}={isinx} \\ $$$${sinx}=\frac{{sinhix}}{{i}}=\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}} \\ $$$${cosx}={coshix}=\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}} \\ $$$${sinx}+{cosx}=\frac{{e}^{{ix}} −{e}^{−{ix}} +{ie}^{{ix}} +{ie}^{−{ix}} }{\mathrm{2}{i}}=\frac{{e}^{{ix}} \left(\mathrm{1}+{i}\right)+{e}^{−{ix}} \left({i}−\mathrm{1}\right)}{\mathrm{2}{i}} \\ $$$${e}^{−{x}} +{sinx}=\frac{\mathrm{2}{ie}^{−{x}} +{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}} \\ $$$${I}=\int\frac{{sinx}+{cosx}}{{e}^{−{x}} +{sinx}}{dx}=\int\frac{{e}^{{ix}} \left({i}+\mathrm{1}\right)+{e}^{−{ix}} \left({i}−\mathrm{1}\right)}{{e}^{{ix}} −{e}^{−{ix}} +\mathrm{2}{ie}^{−{x}} }{dx} \\ $$$${I}=\int\frac{{e}^{{x}} }{{e}^{{x}} }×\frac{{e}^{{ix}} \left({i}+\mathrm{1}\right)+{e}^{−{ix}} \left({i}−\mathrm{1}\right)}{{e}^{{ix}} −{e}^{−{ix}} +\mathrm{2}{ie}^{−{x}} }{dx}=\int\frac{{e}^{{x}\left({i}+\mathrm{1}\right)} \left({i}+\mathrm{1}\right)−{e}^{{x}\left(\mathrm{1}−{i}\right)} \left(\mathrm{1}−{i}\right)}{{e}^{{x}\left({i}+\mathrm{1}\right)} −{e}^{{x}\left(\mathrm{1}−{i}\right)} +\mathrm{2}{i}}{dx} \\ $$$${Let}\:{u}={e}^{{x}\left(\mathrm{1}+{i}\right)} −{e}^{{x}\left(\mathrm{1}−{i}\right)} +\mathrm{2}{i}. \\ $$$$\Rightarrow{du}=\left\{{e}^{{x}\left(\mathrm{1}+{i}\right)} \left({i}+\mathrm{1}\right)−{e}^{{x}\left(\mathrm{1}−{i}\right)} \left(\mathrm{1}−{i}\right)\right\}{dx} \\ $$$$\Rightarrow{I}=\int\frac{{du}}{{u}}={ln}\mid{u}\mid+{C} \\ $$$${I}={ln}\mid{e}^{{x}\left(\mathrm{1}+{i}\right)} −{e}^{{x}\left(\mathrm{1}−{i}\right)} +\mathrm{2}{i}\mid+{C} \\ $$$${u}={e}^{{x}} \left({e}^{{ix}} −{e}^{−{ix}} \right)+\mathrm{2}{i} \\ $$$${u}={e}^{{x}} \left(\mathrm{2}{isinx}\right)+\mathrm{2}{i} \\ $$$${u}=\mathrm{2}{i}\left({e}^{{x}} {sinx}+\mathrm{1}\right) \\ $$$$\therefore\:{I}={ln}\mid\mathrm{2}{i}\left({e}^{{x}} {sinx}+\mathrm{1}\right)\mid+{C} \\ $$$${I}={ln}\mathrm{2}+{ln}\mid{e}^{{x}} {sinx}+\mathrm{1}\mid+{C} \\ $$$$\int\frac{{sinx}+{cosx}}{{e}^{−{x}} +{sinx}}{dx}={ln}\mid{e}^{{x}} {sinx}+\mathrm{1}\mid+{D} \\ $$$${D}={constant} \\ $$$${Checking}: \\ $$$$\frac{{d}}{{dx}}{ln}\left({e}^{{x}} {sinx}+\mathrm{1}\right)=\frac{{e}^{{x}} \left({cosx}+{sinx}\right)}{{e}^{{x}} {sinx}+\mathrm{1}}=\frac{{sinx}+{cosx}}{{sinx}+{e}^{−{x}} } \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${This}\:{answer}\:{suggests}\:{the}\:{folliwing}\:{approach}: \\ $$$${I}=\int\frac{{sinx}+{cosx}}{{e}^{−{x}} +{sinx}}{dx}=\int\frac{{e}^{{x}} \left({sinx}+{cosx}\right)}{\mathrm{1}+{e}^{{x}} {sinx}}{dx}. \\ $$$${Let}\:{u}=\mathrm{1}+{e}^{{x}} {sinx}\Rightarrow{du}={e}^{{x}} \left({cosx}+{sinx}\right){dx} \\ $$$${I}=\int\frac{{du}}{{u}}={ln}\mid{u}\mid={ln}\mid{e}^{{x}} {sinx}+\mathrm{1}\mid+{C}. \\ $$

Commented by Tawakalitu. last updated on 31/Jul/16

Wow ... I really appreciate your effort

$${Wow}\:...\:{I}\:{really}\:{appreciate}\:{your}\:{effort} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com