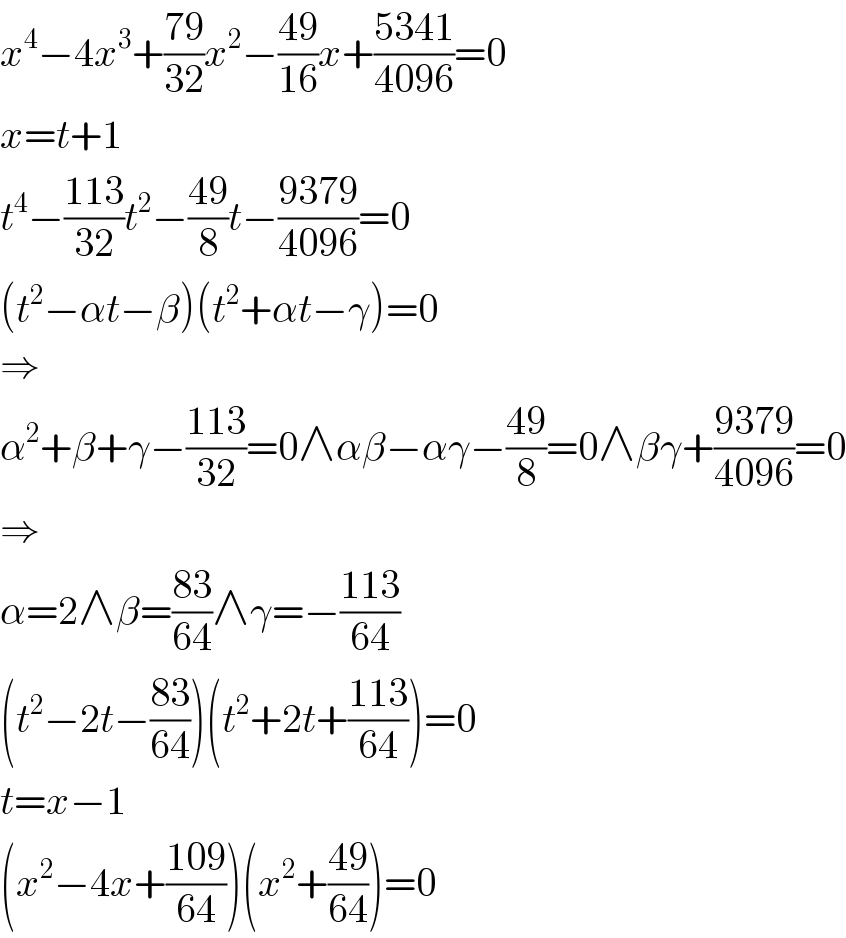The square ABCD has side equal to 1 and the distance AP is (1/8). Calculate the side of the equilateral triangle PMN inscribed in the square.


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 68831 by Maclaurin Stickker last updated on 15/Sep/19

$The square A B C D has side equal to 1$ $and the distance A P is \frac{1}{8} .$ $Calculate the side of the equilateral$ $triangle P M N inscribed in the square .$
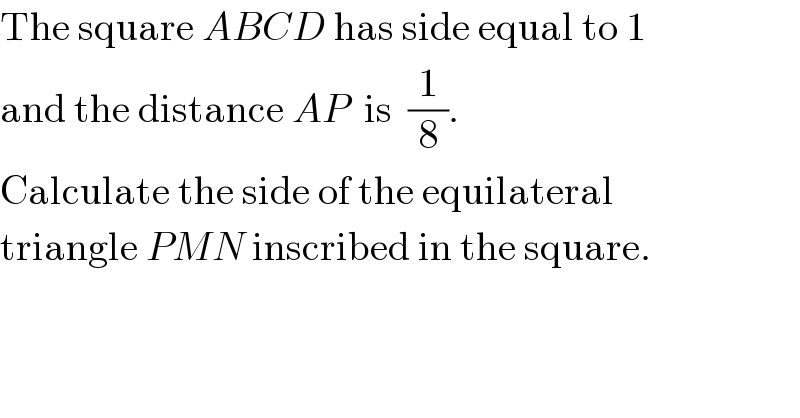
Commented by Maclaurin Stickker last updated on 15/Sep/19

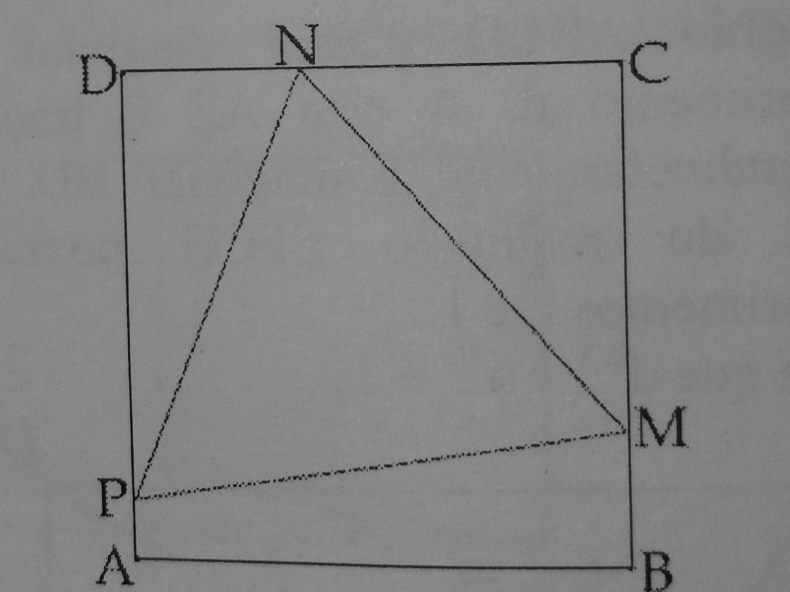
Commented by ajfour last updated on 16/Sep/19

$l e t A P = \frac{1}{8} = a$ $t r i a n g l e s i d e s, s i d e o f s q u a r e 1 .$ $s \cos α = 1$ $D P = s \cos (\frac{π}{6} - α) = 1 - a$ $\Rightarrow \frac{\sqrt{3}}{2} + (\frac{s}{2}) \sin α = 1 - a$ $s \sqrt{1 - \frac{1}{s^{2}}} = \frac{7}{4} - \sqrt{3}$ $s^{2} - 1 = {(\frac{7}{4} - \sqrt{3})}^{2}$ $s^{2} = \frac{49}{16} + 3 - \frac{7 \sqrt{3}}{2} + 1$ $s = \frac{\sqrt{113 - 56 \sqrt{3}}}{4} .$
Commented by Maclaurin Stickker last updated on 16/Sep/19

$W o w . I l o v e d h o w y o u u s e d t r i g o n o m e t r y .$
	Answered by MJS last updated on 16/Sep/19

	$P = (\begin{matrix} 0 \\ \frac{1}{8} \end{matrix}) M = (\begin{matrix} 1 \\ y \end{matrix}) N = (\begin{matrix} x \\ 1 \end{matrix})$ $∣ P M ∣^{2} =∣ P N ∣^{2} =∣ M N ∣^{2}$ $y^{2} - \frac{1}{4} y + \frac{65}{64} = x^{2} + \frac{49}{64} = x^{2} + y^{2} - 2 x - 2 y + 2$ $y^{2} - \frac{1}{4} y + \frac{65}{64} = x^{2} + y^{2} - 2 x - 2 y + 2$ $\Rightarrow y = \frac{4}{7} x^{2} - \frac{8}{7} x + \frac{9}{16}$ $y^{2} - \frac{1}{4} y + \frac{65}{64} = x^{2} + \frac{49}{64}$ $\Rightarrow$ $x^{4} - 4 x^{3} + \frac{79}{32} x^{2} - \frac{49}{16} x + \frac{5341}{4096} = 0$ $(x^{2} + \frac{49}{64}) (x^{2} - 4 x + \frac{109}{64}) = 0$ $x \in [0; 1] \Rightarrow x = 2 - \frac{7 \sqrt{3}}{8} \Rightarrow y = \frac{15}{8} - \sqrt{3}$ $\Rightarrow side s = \frac{\sqrt{113 - 56 \sqrt{3}}}{4}$
	Commented by Maclaurin Stickker last updated on 16/Sep/19

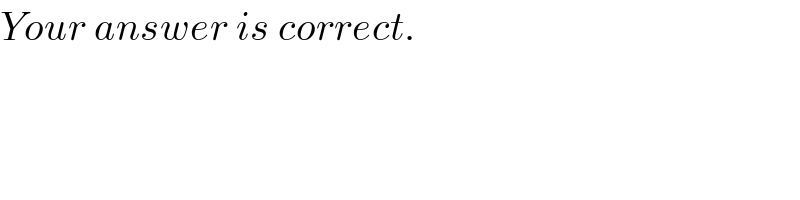
	$Y o u r a n s w e r i s c o r r e c t .$
	Commented by Maclaurin Stickker last updated on 16/Sep/19

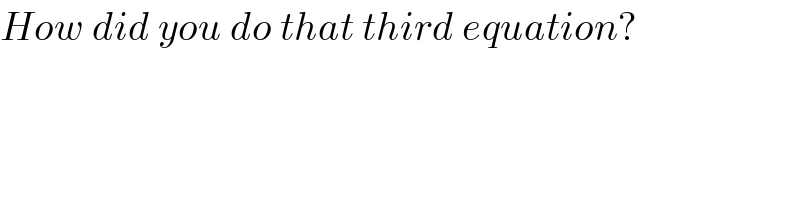
	$H o w d i d y o u d o t h a t t h i r d e q u a t i o n ?$
	Commented by Maclaurin Stickker last updated on 16/Sep/19

	$T h a n k y o u!$
	Commented by MJS last updated on 16/Sep/19

	$x^{4} - 4 x^{3} + \frac{79}{32} x^{2} - \frac{49}{16} x + \frac{5341}{4096} = 0$ $x = t + 1$ $t^{4} - \frac{113}{32} t^{2} - \frac{49}{8} t - \frac{9379}{4096} = 0$ $(t^{2} - α t - β) (t^{2} + α t - γ) = 0$ $\Rightarrow$ $α^{2} + β + γ - \frac{113}{32} = 0 \land α β - α γ - \frac{49}{8} = 0 \land β γ + \frac{9379}{4096} = 0$ $\Rightarrow$ $α = 2 \land β = \frac{83}{64} \land γ = - \frac{113}{64}$ $(t^{2} - 2 t - \frac{83}{64}) (t^{2} + 2 t + \frac{113}{64}) = 0$ $t = x - 1$ $(x^{2} - 4 x + \frac{109}{64}) (x^{2} + \frac{49}{64}) = 0$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum