
Question Number 68960 by ajfour last updated on 17/Sep/19

Commented by TawaTawa last updated on 17/Sep/19

$$\mathrm{Wow},\:\mathrm{weldone}\:\mathrm{sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by ajfour last updated on 17/Sep/19
![a=b=c=d=e=−1 λ^2 −λ−1=0 ⇒ λ=((1±(√5))/2) A=−λ^2 −λ−1=−(2+λ) =−(((5±(√5))/2)) Q_1 =q^2 −q−1 , Q_2 =−q^2 −q−1 L_1 =2λq++b(λ+q)+2d =2(((1±(√5))/2))q−((1±(√5))/2)−q−2 =±(√5)q−(((5±(√5))/2)) L_2 =2aλq+c(λ+q)+2e =−2(((1±(√5))/2))q−((1±(√5))/2)−q−2 =−(2±(√5))q−(((5±(√5))/2)) Now AQ_1 ^2 −L_1 L_2 Q_1 +L_1 ^2 Q_2 =0 −(((5±(√5))/2))(q^2 −q−1)^2 −[±(√5)q−(((5±(√5))/2))][−(2±(√5))q−(((5±(√5))/2))] ×(q^2 −q−1) +[±(√5)q−(((5±(√5))/2))]^2 (−q^2 −q−1)=0 ⇒ −2(5±(√5))(q^2 −q−1)^2 +[±2(√5)q−(5±(√5))][2(2±(√5))q+(5±(√5)] ×(q^2 −q−1) −[±2(√5)q−(5±(√5))]^2 (q^2 +q+1)=0 ⇒ let 5±(√5)=n ⇒ −2n(q^2 −q−1)^2 +[−10q+2nq−n] ×[−6q+2nq+n](q^2 −q−1) −[−10q+2nq−n]^2 (q^2 +q+1)=0 ⇒ −2n(q^2 −q−1)^2 + [(2n−10)(2n−6)q^2 −4nq−n^2 ] ×(q^2 −q−1)+ −[(2n−10)^2 q^2 −2n(2n−10)q+n^2 ] ×(q^2 +q+1) = 0 ⇒ −2n(q^4 −2q^3 −q^2 +2q+1)+ +{4(n−5)(n−3)q^4 −4q^3 [(n−5)(n−3)+n] −q^2 [4(n−5)(n−3)+n^2 −4n] +q(n^2 +4n)+n^2 } −[(2n−10)^2 q^2 −2n(2n−10)q+n^2 ] ×(q^2 +q+1)=0 ⇒ q^4 {−2n+4n^2 −32n+60 −4n^2 +40n−100} +q^3 {4n−4n^2 +28n−60 −4n^2 +40n−100 +4n^2 −20n} +q^2 {2n−5n^2 +36n−60 −4n^2 +40n−100 +4n^2 −20n−n^2 } +q{−4n+n^2 +4n 4n^2 −20n−n^2 } (−2n+n^2 −n^2 )=0 Reducing (6n−40)q^4 −(4n^2 −52n+160)q^3 −(6n^2 −58n+160)q^2 +4(n^2 −5n)q−2n=0 Again dividing by 2 (3n−20)q^4 −(2n^2 −26n+80)q^3 −(3n^2 −29n+80)q^2 +(2n^2 −10n)q−n=0 to remind again n=5±(√5) taking n_1 =5+(√5) n^2 (−2q^3 −3q^2 +2q)+ n(3q^4 +26q^3 +29q^2 −10q−1)+ 1(−20q^4 −80q^3 −80q^2 )=0 since n=5±(√5) (n−5)^2 =5 n^2 −10n+20=0 n^2 =10n−20 So, i can write n(−20q^3 −30q^2 +20q) −20(−2q^3 −3q^2 +2q) n(3q^4 +26q^3 +29q^2 −10q−1)+ 1(−20q^4 −80q^3 −80q^2 )=0 ⇒ n(3q^4 +6q^3 −q^2 +10q−1) +(−20q^4 −40q^3 −20q^2 −40q)=0 ⇒ n(3q^4 +6q^3 −q^2 +10q−1) −20(q^4 +2q^3 +q^2 +2q)=0 ________________________ (3n−20)(q^4 +2q^3 +q^2 +2q) −n(4q^2 −4q+1) = 0 _______________________ 3n−20 = −5±3(√5) = N 6n−40=−10±6(√5) −n−20 = −25∓(√5) = −((N+80)/3) 10n−40 = 10±10(√5) = 10(((N+8)/3)) ⇒ q^4 +2q^3 −(((N+80)/(3N)))q^2 +(((10N+80)/(3N)))q−(((N+20)/(3N)))=0](Q68968.png)
$$ \\ $$$$\:\:\:\:\:\:{a}={b}={c}={d}={e}=−\mathrm{1} \\ $$$$\:\:\lambda^{\mathrm{2}} −\lambda−\mathrm{1}=\mathrm{0}\:\:\Rightarrow\:\lambda=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${A}=−\lambda^{\mathrm{2}} −\lambda−\mathrm{1}=−\left(\mathrm{2}+\lambda\right) \\ $$$$\:\:\:\:=−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$${Q}_{\mathrm{1}} ={q}^{\mathrm{2}} −{q}−\mathrm{1}\:\:\:,\:\:{Q}_{\mathrm{2}} =−{q}^{\mathrm{2}} −{q}−\mathrm{1} \\ $$$${L}_{\mathrm{1}} =\mathrm{2}\lambda{q}++{b}\left(\lambda+{q}\right)+\mathrm{2}{d} \\ $$$$\:\:\:\:=\mathrm{2}\left(\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right){q}−\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}−{q}−\mathrm{2} \\ $$$$\:\:\:\:=\pm\sqrt{\mathrm{5}}{q}−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$${L}_{\mathrm{2}} =\mathrm{2}{a}\lambda{q}+{c}\left(\lambda+{q}\right)+\mathrm{2}{e} \\ $$$$\:\:\:\:\:=−\mathrm{2}\left(\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right){q}−\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}−{q}−\mathrm{2} \\ $$$$\:\:\:\:=−\left(\mathrm{2}\pm\sqrt{\mathrm{5}}\right){q}−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$${Now}\:\:{AQ}_{\mathrm{1}} ^{\mathrm{2}} −{L}_{\mathrm{1}} {L}_{\mathrm{2}} {Q}_{\mathrm{1}} +{L}_{\mathrm{1}} ^{\mathrm{2}} {Q}_{\mathrm{2}} =\mathrm{0} \\ $$$$−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$−\left[\pm\sqrt{\mathrm{5}}{q}−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right]\left[−\left(\mathrm{2}\pm\sqrt{\mathrm{5}}\right){q}−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right] \\ $$$$\:\:\:\:\:\:×\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right) \\ $$$$+\left[\pm\sqrt{\mathrm{5}}{q}−\left(\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right]^{\mathrm{2}} \left(−{q}^{\mathrm{2}} −{q}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:−\mathrm{2}\left(\mathrm{5}\pm\sqrt{\mathrm{5}}\right)\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:+\left[\pm\mathrm{2}\sqrt{\mathrm{5}}{q}−\left(\mathrm{5}\pm\sqrt{\mathrm{5}}\right)\right]\left[\mathrm{2}\left(\mathrm{2}\pm\sqrt{\mathrm{5}}\right){q}+\left(\mathrm{5}\pm\sqrt{\mathrm{5}}\right]\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:×\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right) \\ $$$$−\left[\pm\mathrm{2}\sqrt{\mathrm{5}}{q}−\left(\mathrm{5}\pm\sqrt{\mathrm{5}}\right)\right]^{\mathrm{2}} \left({q}^{\mathrm{2}} +{q}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\:{let}\:\:\mathrm{5}\pm\sqrt{\mathrm{5}}={n}\:\:\:\:\Rightarrow \\ $$$$\:−\mathrm{2}{n}\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right)^{\mathrm{2}} +\left[−\mathrm{10}{q}+\mathrm{2}{nq}−{n}\right] \\ $$$$\:\:\:\:\:\:×\left[−\mathrm{6}{q}+\mathrm{2}{nq}+{n}\right]\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right) \\ $$$$−\left[−\mathrm{10}{q}+\mathrm{2}{nq}−{n}\right]^{\mathrm{2}} \left({q}^{\mathrm{2}} +{q}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\:−\mathrm{2}{n}\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right)^{\mathrm{2}} + \\ $$$$\:\left[\left(\mathrm{2}{n}−\mathrm{10}\right)\left(\mathrm{2}{n}−\mathrm{6}\right){q}^{\mathrm{2}} −\mathrm{4}{nq}−{n}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:×\left({q}^{\mathrm{2}} −{q}−\mathrm{1}\right)+ \\ $$$$\:\:\:\:\:−\left[\left(\mathrm{2}{n}−\mathrm{10}\right)^{\mathrm{2}} {q}^{\mathrm{2}} −\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{10}\right){q}+{n}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:×\left({q}^{\mathrm{2}} +{q}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\:\:−\mathrm{2}{n}\left({q}^{\mathrm{4}} −\mathrm{2}{q}^{\mathrm{3}} −{q}^{\mathrm{2}} +\mathrm{2}{q}+\mathrm{1}\right)+ \\ $$$$\:+\left\{\mathrm{4}\left({n}−\mathrm{5}\right)\left({n}−\mathrm{3}\right){q}^{\mathrm{4}} \right. \\ $$$$\:\:\:\:−\mathrm{4}{q}^{\mathrm{3}} \left[\left({n}−\mathrm{5}\right)\left({n}−\mathrm{3}\right)+{n}\right] \\ $$$$\:\:\:−{q}^{\mathrm{2}} \left[\mathrm{4}\left({n}−\mathrm{5}\right)\left({n}−\mathrm{3}\right)+{n}^{\mathrm{2}} −\mathrm{4}{n}\right] \\ $$$$\left.\:\:\:\:+{q}\left({n}^{\mathrm{2}} +\mathrm{4}{n}\right)+{n}^{\mathrm{2}} \right\} \\ $$$$\:−\left[\left(\mathrm{2}{n}−\mathrm{10}\right)^{\mathrm{2}} {q}^{\mathrm{2}} −\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{10}\right){q}+{n}^{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:×\left({q}^{\mathrm{2}} +{q}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${q}^{\mathrm{4}} \left\{−\mathrm{2}{n}+\mathrm{4}{n}^{\mathrm{2}} −\mathrm{32}{n}+\mathrm{60}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:−\mathrm{4}{n}^{\mathrm{2}} +\mathrm{40}{n}−\mathrm{100}\right\} \\ $$$$+{q}^{\mathrm{3}} \left\{\mathrm{4}{n}−\mathrm{4}{n}^{\mathrm{2}} +\mathrm{28}{n}−\mathrm{60}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{n}^{\mathrm{2}} +\mathrm{40}{n}−\mathrm{100} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{4}{n}^{\mathrm{2}} −\mathrm{20}{n}\right\} \\ $$$$+{q}^{\mathrm{2}} \left\{\mathrm{2}{n}−\mathrm{5}{n}^{\mathrm{2}} +\mathrm{36}{n}−\mathrm{60}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{n}^{\mathrm{2}} +\mathrm{40}{n}−\mathrm{100} \\ $$$$\left.\:\:\:\:\:\:\:\:\:+\mathrm{4}{n}^{\mathrm{2}} −\mathrm{20}{n}−{n}^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:+{q}\left\{−\mathrm{4}{n}+{n}^{\mathrm{2}} +\mathrm{4}{n}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{n}^{\mathrm{2}} −\mathrm{20}{n}−{n}^{\mathrm{2}} \right\} \\ $$$$\:\:\left(−\mathrm{2}{n}+{n}^{\mathrm{2}} −{n}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${Reducing} \\ $$$$\:\:\left(\mathrm{6}{n}−\mathrm{40}\right){q}^{\mathrm{4}} −\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{52}{n}+\mathrm{160}\right){q}^{\mathrm{3}} \\ $$$$\:\:\:−\left(\mathrm{6}{n}^{\mathrm{2}} −\mathrm{58}{n}+\mathrm{160}\right){q}^{\mathrm{2}} \\ $$$$\:\:\:+\mathrm{4}\left({n}^{\mathrm{2}} −\mathrm{5}{n}\right){q}−\mathrm{2}{n}=\mathrm{0} \\ $$$${Again}\:\:{dividing}\:{by}\:\mathrm{2} \\ $$$$\:\left(\mathrm{3}{n}−\mathrm{20}\right){q}^{\mathrm{4}} −\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{26}{n}+\mathrm{80}\right){q}^{\mathrm{3}} \\ $$$$\:\:−\left(\mathrm{3}{n}^{\mathrm{2}} −\mathrm{29}{n}+\mathrm{80}\right){q}^{\mathrm{2}} \\ $$$$\:\:\:+\left(\mathrm{2}{n}^{\mathrm{2}} −\mathrm{10}{n}\right){q}−{n}=\mathrm{0} \\ $$$${to}\:{remind}\:{again}\:\:\:{n}=\mathrm{5}\pm\sqrt{\mathrm{5}} \\ $$$$\:\:{taking}\:{n}_{\mathrm{1}} =\mathrm{5}+\sqrt{\mathrm{5}} \\ $$$${n}^{\mathrm{2}} \left(−\mathrm{2}{q}^{\mathrm{3}} −\mathrm{3}{q}^{\mathrm{2}} +\mathrm{2}{q}\right)+ \\ $$$${n}\left(\mathrm{3}{q}^{\mathrm{4}} +\mathrm{26}{q}^{\mathrm{3}} +\mathrm{29}{q}^{\mathrm{2}} −\mathrm{10}{q}−\mathrm{1}\right)+ \\ $$$$\mathrm{1}\left(−\mathrm{20}{q}^{\mathrm{4}} −\mathrm{80}{q}^{\mathrm{3}} −\mathrm{80}{q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${since}\:\:{n}=\mathrm{5}\pm\sqrt{\mathrm{5}} \\ $$$$\left({n}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{5} \\ $$$${n}^{\mathrm{2}} −\mathrm{10}{n}+\mathrm{20}=\mathrm{0} \\ $$$${n}^{\mathrm{2}} =\mathrm{10}{n}−\mathrm{20}\:\:\:{So},\:{i}\:{can}\:{write} \\ $$$${n}\left(−\mathrm{20}{q}^{\mathrm{3}} −\mathrm{30}{q}^{\mathrm{2}} +\mathrm{20}{q}\right) \\ $$$$−\mathrm{20}\left(−\mathrm{2}{q}^{\mathrm{3}} −\mathrm{3}{q}^{\mathrm{2}} +\mathrm{2}{q}\right) \\ $$$${n}\left(\mathrm{3}{q}^{\mathrm{4}} +\mathrm{26}{q}^{\mathrm{3}} +\mathrm{29}{q}^{\mathrm{2}} −\mathrm{10}{q}−\mathrm{1}\right)+ \\ $$$$\mathrm{1}\left(−\mathrm{20}{q}^{\mathrm{4}} −\mathrm{80}{q}^{\mathrm{3}} −\mathrm{80}{q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${n}\left(\mathrm{3}{q}^{\mathrm{4}} +\mathrm{6}{q}^{\mathrm{3}} −{q}^{\mathrm{2}} +\mathrm{10}{q}−\mathrm{1}\right) \\ $$$$+\left(−\mathrm{20}{q}^{\mathrm{4}} −\mathrm{40}{q}^{\mathrm{3}} −\mathrm{20}{q}^{\mathrm{2}} −\mathrm{40}{q}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{n}\left(\mathrm{3}{q}^{\mathrm{4}} +\mathrm{6}{q}^{\mathrm{3}} −{q}^{\mathrm{2}} +\mathrm{10}{q}−\mathrm{1}\right) \\ $$$$\:\:−\mathrm{20}\left({q}^{\mathrm{4}} +\mathrm{2}{q}^{\mathrm{3}} +{q}^{\mathrm{2}} +\mathrm{2}{q}\right)=\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\left(\mathrm{3}{n}−\mathrm{20}\right)\left({q}^{\mathrm{4}} +\mathrm{2}{q}^{\mathrm{3}} +{q}^{\mathrm{2}} +\mathrm{2}{q}\right) \\ $$$$\:−{n}\left(\mathrm{4}{q}^{\mathrm{2}} −\mathrm{4}{q}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\mathrm{3}{n}−\mathrm{20}\:=\:−\mathrm{5}\pm\mathrm{3}\sqrt{\mathrm{5}}\:=\:{N} \\ $$$$\mathrm{6}{n}−\mathrm{40}=−\mathrm{10}\pm\mathrm{6}\sqrt{\mathrm{5}} \\ $$$$−{n}−\mathrm{20}\:=\:−\mathrm{25}\mp\sqrt{\mathrm{5}}\:=\:−\frac{{N}+\mathrm{80}}{\mathrm{3}} \\ $$$$\mathrm{10}{n}−\mathrm{40}\:=\:\mathrm{10}\pm\mathrm{10}\sqrt{\mathrm{5}}\:=\:\mathrm{10}\left(\frac{{N}+\mathrm{8}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\:\:\: \\ $$$${q}^{\mathrm{4}} +\mathrm{2}{q}^{\mathrm{3}} −\left(\frac{{N}+\mathrm{80}}{\mathrm{3}{N}}\right){q}^{\mathrm{2}} \\ $$$$\:\:\:\:\:+\left(\frac{\mathrm{10}{N}+\mathrm{80}}{\mathrm{3}{N}}\right){q}−\left(\frac{{N}+\mathrm{20}}{\mathrm{3}{N}}\right)=\mathrm{0} \\ $$
Commented by TawaTawa last updated on 17/Sep/19
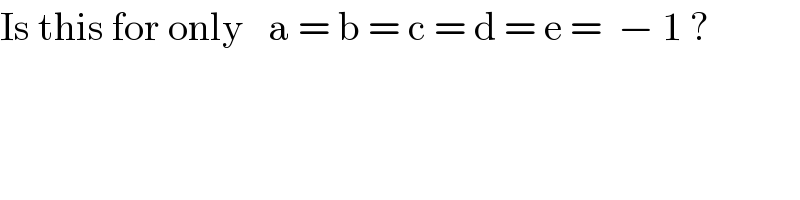
$$\mathrm{Is}\:\mathrm{this}\:\mathrm{for}\:\mathrm{only}\:\:\:\mathrm{a}\:=\:\mathrm{b}\:=\:\mathrm{c}\:=\:\mathrm{d}\:=\:\mathrm{e}\:=\:\:−\:\mathrm{1}\:? \\ $$
