Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 69046 by Rio Michael last updated on 18/Sep/19

Commented by mathmax by abdo last updated on 18/Sep/19

4)we have y=xarctanx ⇒y^′ =arctanx +(x/(1+x^2 )) ⇒ (x+x^3 )y^′ −(1+x^2 )y−x^2 =(x+x^3 )arctanx +x^2 −(1+x^2 )xarctanx −x^2 =0 ⇒(x+x^3 ) y^′ =(1+x^2 )y+x^2 ⇒let derivate (1+3x^2 )y^′ +(x+x^3 )y^(′′) =2x y+(1+x^2 )y^′ +2x ⇒ (x+x^3 )y^(′′) +(1+3x^2 −1−x^2 )y^′ −2xy −2x =0 ⇒ x(1+x^2 )y^(′′) +2x^2 y^′ −2x(y+1) =0 ⇒ (1+x^2 )y^(′′) +2xy^′ −2(y+1) =0

$$\left.\mathrm{4}\right){we}\:{have}\:\:{y}={xarctanx}\:\Rightarrow{y}^{'} ={arctanx}\:+\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\left({x}+{x}^{\mathrm{3}} \right){y}^{'} −\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}−{x}^{\mathrm{2}} =\left({x}+{x}^{\mathrm{3}} \right){arctanx}\:\:+{x}^{\mathrm{2}} −\left(\mathrm{1}+{x}^{\mathrm{2}} \right){xarctanx} \\ $$$$−{x}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\left({x}+{x}^{\mathrm{3}} \right)\:{y}^{'} \:=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}+{x}^{\mathrm{2}} \:\Rightarrow{let}\:{derivate} \\ $$$$\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} \right){y}^{'} \:+\left({x}+{x}^{\mathrm{3}} \right){y}^{''} =\mathrm{2}{x}\:{y}+\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \:+\mathrm{2}{x}\:\Rightarrow \\ $$$$\left({x}+{x}^{\mathrm{3}} \right){y}^{''} \:\:+\left(\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}−{x}^{\mathrm{2}} \right){y}^{'} \:−\mathrm{2}{xy}\:−\mathrm{2}{x}\:=\mathrm{0}\:\Rightarrow \\ $$$${x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{''} \:+\mathrm{2}{x}^{\mathrm{2}} {y}^{'} −\mathrm{2}{x}\left({y}+\mathrm{1}\right)\:=\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{''} \:+\mathrm{2}{xy}^{'} −\mathrm{2}\left({y}+\mathrm{1}\right)\:=\mathrm{0} \\ $$

Commented by Rio Michael last updated on 18/Sep/19

thanks sir

$${thanks}\:{sir} \\ $$

Commented by mathmax by abdo last updated on 18/Sep/19

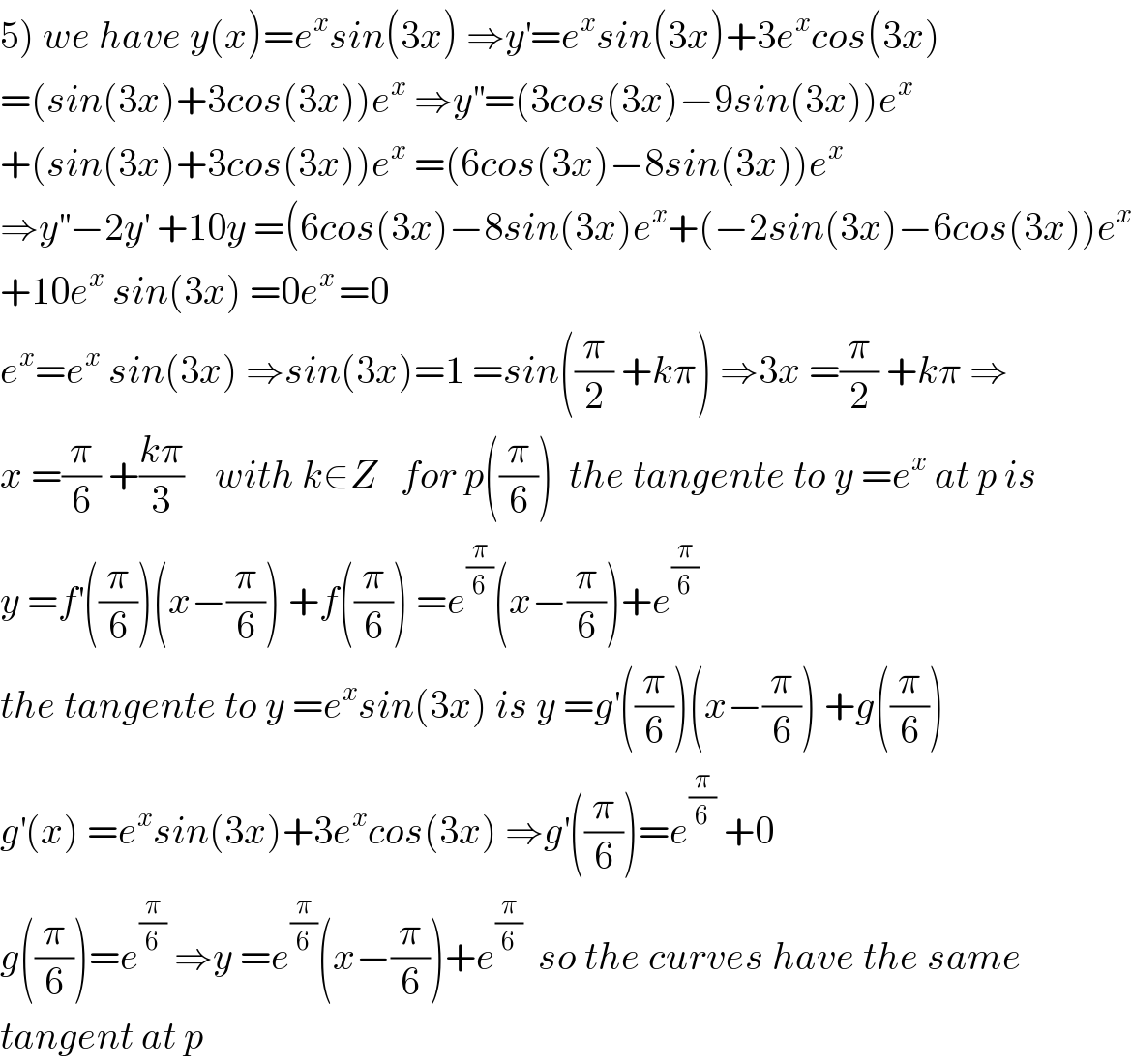
5) we have y(x)=e^x sin(3x) ⇒y^′ =e^x sin(3x)+3e^x cos(3x) =(sin(3x)+3cos(3x))e^x ⇒y^(′′) =(3cos(3x)−9sin(3x))e^x +(sin(3x)+3cos(3x))e^x =(6cos(3x)−8sin(3x))e^x ⇒y^(′′) −2y^′ +10y =(6cos(3x)−8sin(3x)e^x +(−2sin(3x)−6cos(3x))e^x +10e^x sin(3x) =0e^(x ) =0 e^x =e^x sin(3x) ⇒sin(3x)=1 =sin((π/2) +kπ) ⇒3x =(π/2) +kπ ⇒ x =(π/6) +((kπ)/3) with k∈Z for p((π/6)) the tangente to y =e^x at p is y =f^′ ((π/6))(x−(π/6)) +f((π/6)) =e^(π/6) (x−(π/6))+e^(π/6) the tangente to y =e^x sin(3x) is y =g^′ ((π/6))(x−(π/6)) +g((π/6)) g^′ (x) =e^x sin(3x)+3e^x cos(3x) ⇒g^′ ((π/6))=e^(π/6) +0 g((π/6))=e^(π/6) ⇒y =e^(π/6) (x−(π/6))+e^(π/6) so the curves have the same tangent at p

$$\left.\mathrm{5}\right)\:{we}\:{have}\:{y}\left({x}\right)={e}^{{x}} {sin}\left(\mathrm{3}{x}\right)\:\Rightarrow{y}^{'} ={e}^{{x}} {sin}\left(\mathrm{3}{x}\right)+\mathrm{3}{e}^{{x}} {cos}\left(\mathrm{3}{x}\right) \\ $$$$=\left({sin}\left(\mathrm{3}{x}\right)+\mathrm{3}{cos}\left(\mathrm{3}{x}\right)\right){e}^{{x}} \:\Rightarrow{y}^{''} =\left(\mathrm{3}{cos}\left(\mathrm{3}{x}\right)−\mathrm{9}{sin}\left(\mathrm{3}{x}\right)\right){e}^{{x}} \\ $$$$+\left({sin}\left(\mathrm{3}{x}\right)+\mathrm{3}{cos}\left(\mathrm{3}{x}\right)\right){e}^{{x}} \:=\left(\mathrm{6}{cos}\left(\mathrm{3}{x}\right)−\mathrm{8}{sin}\left(\mathrm{3}{x}\right)\right){e}^{{x}} \\ $$$$\Rightarrow{y}^{''} −\mathrm{2}{y}^{'} \:+\mathrm{10}{y}\:=\left(\mathrm{6}{cos}\left(\mathrm{3}{x}\right)−\mathrm{8}{sin}\left(\mathrm{3}{x}\right){e}^{{x}} +\left(−\mathrm{2}{sin}\left(\mathrm{3}{x}\right)−\mathrm{6}{cos}\left(\mathrm{3}{x}\right)\right){e}^{{x}} \right. \\ $$$$+\mathrm{10}{e}^{{x}} \:{sin}\left(\mathrm{3}{x}\right)\:=\mathrm{0}{e}^{{x}\:} =\mathrm{0} \\ $$$${e}^{{x}} ={e}^{{x}} \:{sin}\left(\mathrm{3}{x}\right)\:\Rightarrow{sin}\left(\mathrm{3}{x}\right)=\mathrm{1}\:={sin}\left(\frac{\pi}{\mathrm{2}}\:+{k}\pi\right)\:\Rightarrow\mathrm{3}{x}\:=\frac{\pi}{\mathrm{2}}\:+{k}\pi\:\Rightarrow \\ $$$${x}\:=\frac{\pi}{\mathrm{6}}\:+\frac{{k}\pi}{\mathrm{3}}\:\:\:\:{with}\:{k}\in{Z}\:\:\:{for}\:{p}\left(\frac{\pi}{\mathrm{6}}\right)\:\:{the}\:{tangente}\:{to}\:{y}\:={e}^{{x}} \:{at}\:{p}\:{is} \\ $$$${y}\:={f}^{'} \left(\frac{\pi}{\mathrm{6}}\right)\left({x}−\frac{\pi}{\mathrm{6}}\right)\:+{f}\left(\frac{\pi}{\mathrm{6}}\right)\:={e}^{\frac{\pi}{\mathrm{6}}} \left({x}−\frac{\pi}{\mathrm{6}}\right)+{e}^{\frac{\pi}{\mathrm{6}}} \\ $$$${the}\:{tangente}\:{to}\:{y}\:={e}^{{x}} {sin}\left(\mathrm{3}{x}\right)\:{is}\:{y}\:={g}^{'} \left(\frac{\pi}{\mathrm{6}}\right)\left({x}−\frac{\pi}{\mathrm{6}}\right)\:+{g}\left(\frac{\pi}{\mathrm{6}}\right) \\ $$$${g}^{'} \left({x}\right)\:={e}^{{x}} {sin}\left(\mathrm{3}{x}\right)+\mathrm{3}{e}^{{x}} {cos}\left(\mathrm{3}{x}\right)\:\Rightarrow{g}^{'} \left(\frac{\pi}{\mathrm{6}}\right)={e}^{\frac{\pi}{\mathrm{6}}} \:+\mathrm{0} \\ $$$${g}\left(\frac{\pi}{\mathrm{6}}\right)={e}^{\frac{\pi}{\mathrm{6}}} \:\Rightarrow{y}\:={e}^{\frac{\pi}{\mathrm{6}}} \left({x}−\frac{\pi}{\mathrm{6}}\right)+{e}^{\frac{\pi}{\mathrm{6}}} \:\:{so}\:{the}\:{curves}\:{have}\:{the}\:{same} \\ $$$${tangent}\:{at}\:{p} \\ $$

Commented by mathmax by abdo last updated on 18/Sep/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com