
Question Number 6935 by FilupSmith last updated on 05/Aug/16
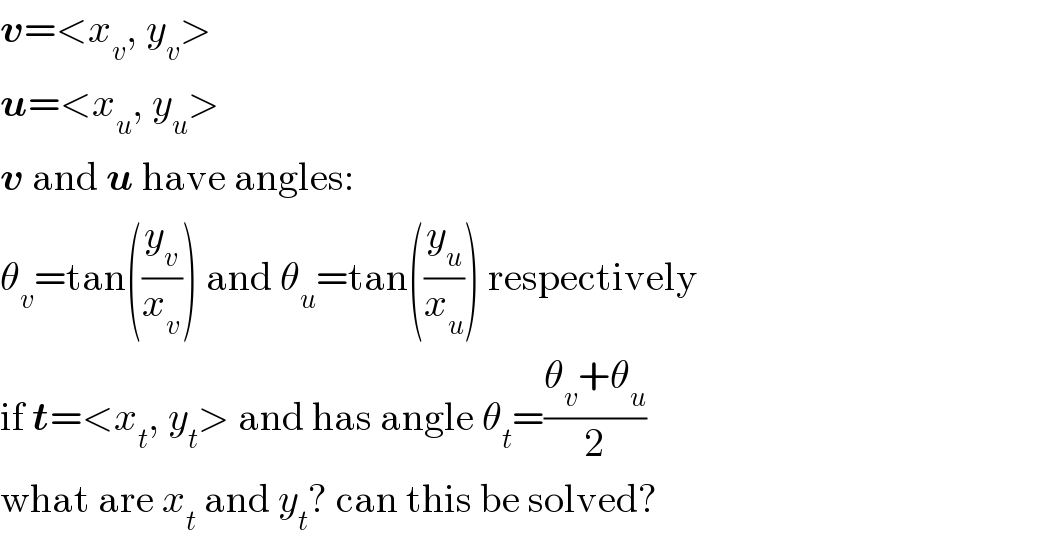
$$\boldsymbol{{v}}=<{x}_{{v}} ,\:{y}_{{v}} > \\ $$ $$\boldsymbol{{u}}=<{x}_{{u}} ,\:{y}_{{u}} > \\ $$ $$\boldsymbol{{v}}\:\mathrm{and}\:\boldsymbol{{u}}\:\mathrm{have}\:\mathrm{angles}: \\ $$ $$\theta_{{v}} =\mathrm{tan}\left(\frac{{y}_{{v}} }{{x}_{{v}} }\right)\:\mathrm{and}\:\theta_{{u}} =\mathrm{tan}\left(\frac{{y}_{{u}} }{{x}_{{u}} }\right)\:\mathrm{respectively} \\ $$ $$\mathrm{if}\:\boldsymbol{{t}}=<{x}_{{t}} ,\:{y}_{{t}} >\:\mathrm{and}\:\mathrm{has}\:\mathrm{angle}\:\theta_{{t}} =\frac{\theta_{{v}} +\theta_{{u}} }{\mathrm{2}} \\ $$ $$\mathrm{what}\:\mathrm{are}\:{x}_{{t}} \:\mathrm{and}\:{y}_{{t}} ?\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{solved}? \\ $$
Answered by nburiburu last updated on 04/Aug/16

$${if}\:{the}\:{angle}\:{of}\:{t}\:{is}\:{an}\:{average}\:{of}\:\:{u}\:{and}\:{v} \\ $$ $${then}\:{you}\:{could}\:{try}\:\:{find}\:\:{cos}\left(\theta_{{t}} \right)\:{and}\:{sin}\left(\theta_{{t}} \right) \\ $$ $${but}\:{if}\:{you}\:{remember}\:{adition}\:{of}\:{vectors} \\ $$ $${then}\:{t}\:{could}\:{be}\:{define}\:{as} \\ $$ $${t}\:=\frac{{u}}{\parallel{u}\parallel}+\frac{{v}}{\parallel{v}\parallel}\: \\ $$ $${since}\:{both}\:{have}\:{same}\:{length},\:{the}\:{diagonal} \\ $$ $${of}\:{the}\:{parallelogram}\:{with}\:{u}\:{and}\:{v}\:{as}\:{sides} \\ $$ $${has}\:{the}\:{average}\:{of}\:{angles}. \\ $$ $$ \\ $$ $${Of}\:{course},\:{there}\:{is}\:{more}\:{than}\:{one}\:{solution} \\ $$ $${but}\:{every}\:{solution}\:{shall}\:{be}\:{a}\:{proportional} \\ $$ $${vector}\:{to}\:{this}\:{one}. \\ $$ $$ \\ $$ $$ \\ $$ $$ \\ $$
