Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 6939 by sou1618 last updated on 03/Aug/16

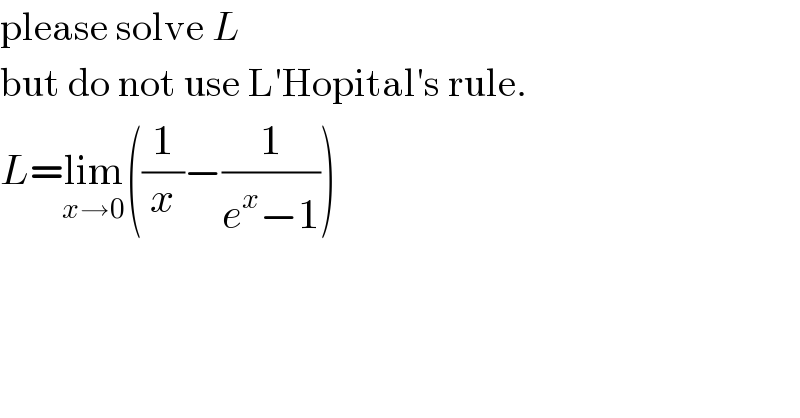
please solve L but do not use L′Hopital′s rule. L=lim_(x→0) ((1/x)−(1/(e^x −1)))

$$\mathrm{please}\:\mathrm{solve}\:{L} \\ $$$$\mathrm{but}\:\mathrm{do}\:\mathrm{not}\:\mathrm{use}\:\mathrm{L}'\mathrm{Hopital}'\mathrm{s}\:\mathrm{rule}. \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right) \\ $$

Commented by Yozzii last updated on 03/Aug/16

(1/x)−(1/(e^x −1))=((e^x −1−x)/(x(e^x −1)))=(((e^x −1−x)/x^2 )/((e^x /x)−(1/x))) e^x −1−x=(x^2 /(2!))+(x^3 /(3!))+(x^4 /(4!))+... ⇒((e^x −1−x)/x^2 )=(1/2)+(x/(3!))+(x^2 /(4!))+(x^3 /(5!))+... (e^x /x)−(1/x)=−(1/x)+(1/x)+1+(x/(2!))+(x^2 /(3!))+(x^3 /(4!))+... (e^x /x)−(1/x)=1+(x/(2!))+(x^2 /(3!))+(x^3 /(4!))+... ∴L=lim_(x→0) ((1/x)−(1/(e^x −1)))=lim_(x→0) (((1/2)+(x/(3!))+(x^2 /(4!))+(x^3 /(5!))+...)/(1+(x/(2!))+(x^2 /(3!))+(x^3 /(4!))+...)) L=(((1/2)+0+0+0+...)/(1+0+0+0+...))=(1/2)

$$\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{e}^{{x}} −\mathrm{1}}=\frac{{e}^{{x}} −\mathrm{1}−{x}}{{x}\left({e}^{{x}} −\mathrm{1}\right)}=\frac{\frac{{e}^{{x}} −\mathrm{1}−{x}}{{x}^{\mathrm{2}} }}{\frac{{e}^{{x}} }{{x}}−\frac{\mathrm{1}}{{x}}} \\ $$$${e}^{{x}} −\mathrm{1}−{x}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+...\: \\ $$$$\Rightarrow\frac{{e}^{{x}} −\mathrm{1}−{x}}{{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{{x}}{\mathrm{3}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{5}!}+...\: \\ $$$$\frac{{e}^{{x}} }{{x}}−\frac{\mathrm{1}}{{x}}=−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}}+\mathrm{1}+\frac{{x}}{\mathrm{2}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{4}!}+... \\ $$$$\frac{{e}^{{x}} }{{x}}−\frac{\mathrm{1}}{{x}}=\mathrm{1}+\frac{{x}}{\mathrm{2}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{4}!}+... \\ $$$$\therefore{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{x}}{\mathrm{3}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{5}!}+...}{\mathrm{1}+\frac{{x}}{\mathrm{2}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{4}!}+...} \\ $$$${L}=\frac{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{0}+\mathrm{0}+\mathrm{0}+...}{\mathrm{1}+\mathrm{0}+\mathrm{0}+\mathrm{0}+...}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Commented by sou1618 last updated on 03/Aug/16

Thank you very much

$${Thank}\:{you}\:{very}\:{much} \\ $$

Answered by Yozzii last updated on 03/Aug/16

Check answer in comments...

$${Check}\:{answer}\:{in}\:{comments}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com