
Question Number 6947 by Tawakalitu. last updated on 03/Aug/16
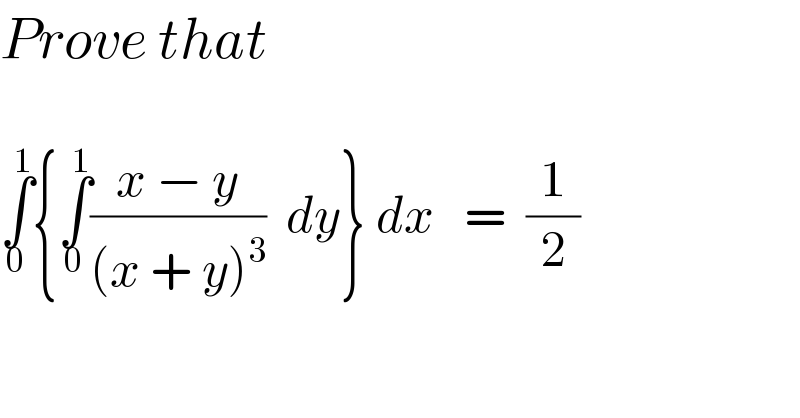
$${Prove}\:{that}\: \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left\{\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{x}\:−\:{y}}{\left({x}\:+\:{y}\right)^{\mathrm{3}} }\:\:{dy}\right\}\:{dx}\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Yozzii last updated on 03/Aug/16
![Q(x)=∫_0 ^1 ((x−y)/((x+y)^3 ))dy Let u=x+y⇒du=dy ⇒y=u−x At y=0,u=x; at y=1,u=x+1 ∴Q(x)=∫_x ^(x+1) ((x−(u−x))/u^3 )du Q(x)=∫_x ^(x+1) u^(−3) (2x−u)du=∫_x ^(x+1) (2xu^(−3) −u^(−2) )du Q(x)=((2xu^(−2) )/(−2))−(u^(−1) /(−1))∣_x ^(x+1) Q(x)=(1/u)−(x/u^2 )∣_x ^(x+1) Q(x)=(1/(x+1))−(x/((x+1)^2 ))−(1/x)+(x/x^2 ) Q(x)=(1/(x+1))−((2(x+1−1))/(2(x+1)^2 )) Q(x)=(1/(x+1))+(1/((x+1)^2 ))−(1/2)(((2(x+1))/((x+1)^2 ))) ∴I=∫_0 ^1 {∫_0 ^1 ((x−y)/((x+y)^3 ))dy}dx=∫_0 ^1 Q(x)dx I=[ln∣x+1∣−(1/(x+1))−(1/2)ln∣(x+1)^2 ∣]_0 ^1 I=[ln∣x+1∣−(1/(x+1))−(1/2)×2×ln∣x+1∣]_0 ^1 I=((−1)/(x+1))∣_0 ^1 =((−1)/2)−(((−1)/1))=1−(1/2)=(1/2). ∴ ∫_0 ^1 ∫_0 ^1 ((x−y)/((x+y)^3 ))dydx=(1/2).](Q6968.png)
$${Q}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−{y}}{\left({x}+{y}\right)^{\mathrm{3}} }{dy} \\ $$$${Let}\:{u}={x}+{y}\Rightarrow{du}={dy} \\ $$$$\Rightarrow{y}={u}−{x} \\ $$$${At}\:{y}=\mathrm{0},{u}={x};\:{at}\:{y}=\mathrm{1},{u}={x}+\mathrm{1} \\ $$$$\therefore{Q}\left({x}\right)=\int_{{x}} ^{{x}+\mathrm{1}} \frac{{x}−\left({u}−{x}\right)}{{u}^{\mathrm{3}} }{du} \\ $$$${Q}\left({x}\right)=\int_{{x}} ^{{x}+\mathrm{1}} {u}^{−\mathrm{3}} \left(\mathrm{2}{x}−{u}\right){du}=\int_{{x}} ^{{x}+\mathrm{1}} \left(\mathrm{2}{xu}^{−\mathrm{3}} −{u}^{−\mathrm{2}} \right){du} \\ $$$${Q}\left({x}\right)=\frac{\mathrm{2}{xu}^{−\mathrm{2}} }{−\mathrm{2}}−\frac{{u}^{−\mathrm{1}} }{−\mathrm{1}}\mid_{{x}} ^{{x}+\mathrm{1}} \\ $$$${Q}\left({x}\right)=\frac{\mathrm{1}}{{u}}−\frac{{x}}{{u}^{\mathrm{2}} }\mid_{{x}} ^{{x}+\mathrm{1}} \\ $$$${Q}\left({x}\right)=\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{{x}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}+\frac{{x}}{{x}^{\mathrm{2}} } \\ $$$${Q}\left({x}\right)=\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{2}\left({x}+\mathrm{1}−\mathrm{1}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${Q}\left({x}\right)=\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}\left({x}+\mathrm{1}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\therefore{I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left\{\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{x}−{y}}{\left({x}+{y}\right)^{\mathrm{3}} }{dy}\right\}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {Q}\left({x}\right){dx} \\ $$$${I}=\left[{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\left({x}+\mathrm{1}\right)^{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}=\left[{ln}\mid{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×{ln}\mid{x}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}=\frac{−\mathrm{1}}{{x}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{−\mathrm{1}}{\mathrm{2}}−\left(\frac{−\mathrm{1}}{\mathrm{1}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−{y}}{\left({x}+{y}\right)^{\mathrm{3}} }{dydx}=\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 03/Aug/16
$${You}\:{are}\:{making}\:{my}\:{day}...\:{Thanks}\:{so}\:{much}..\:{am}\:{really}\:{happy} \\ $$
