Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 93634 by abdomathmax last updated on 14/May/20

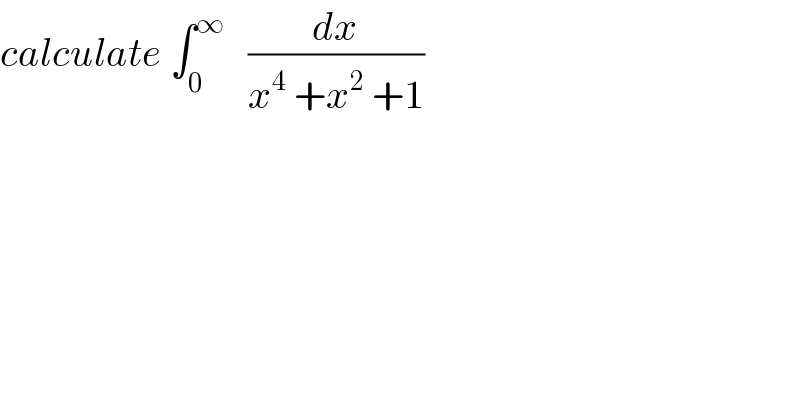
calculate ∫_0 ^∞ (dx/(x^4 +x^2 +1))

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$

Commented by mathmax by abdo last updated on 14/May/20

I =∫_0 ^∞ (dx/(x^4 +x^2 +1)) ⇒2A =∫_(−∞) ^(+∞) (dx/(x^4 +x^2 +1)) let ϕ(z) =(1/(z^4 +z^2 +1)) poles of ϕ? z^4 +z^2 +1 =0 →t^2 +t +1 =0 (t=z^2 ) Δ=−3 ⇒t_1 =((−1+i(√3))/2) =e^((i2π)/3) , t_2 =((−1−i(√3))/2) =e^(−((i2π)/3)) ⇒ ϕ(z) =(1/((z^2 −e^((i2π)/3) )(z^2 −e^(−((i2π)/3)) ))) =(1/((z−e^((iπ)/3) )(z+e^((iπ)/3) )(z−e^((−iπ)/3) )(z+e^(−((iπ)/3)) ))) rdsidus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/3) )+Res(ϕ,−e^(−((iπ)/3)) )} Res(ϕ,e^((iπ)/3) ) =(1/(2e^((iπ)/3) (2isin(((2π)/3))))) =(e^(−((iπ)/3)) /(4i×((√3)/2))) =(e^(−((iπ)/3)) /(2i(√3))) Res(ϕ,−e^(−((iπ)/3)) ) =(1/(−2e^(−((iπ)/3)) (−2i sin(((2π)/3))))) =(e^((iπ)/3) /(4i ×((√3)/2))) =(e^((iπ)/3) /(2i(√3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =((2iπ)/(2i(√3))){ e^(−((iπ)/3)) +e^((iπ)/3) } =(π/(√3))(2cos((π/3))) =(π/(√3)) 2∫_(−∞) ^(+∞) (dx/(x^4 +x^2 +1)) =(π/(√3)) ⇒★∫_(−∞) ^(+∞) (dx/(x^4 +x^2 +1)) =(π/(2(√3))) ★

$${I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:{let}\:\varphi\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${poles}\:{of}\:\varphi?\:\:\: \\ $$$${z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\rightarrow{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}\:=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=−\mathrm{3}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\:\:,\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)}\:=\frac{\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{\frac{−{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$${rdsidus}\:{theorem}\:{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \:\right)+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:=\frac{\mathrm{1}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \left(\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{4}{i}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:=\frac{\mathrm{1}}{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \left(−\mathrm{2}{i}\:{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{4}{i}\:×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\mathrm{2}{i}\pi}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{\:{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right\}\:=\frac{\pi}{\sqrt{\mathrm{3}}}\left(\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\right)\:=\frac{\pi}{\sqrt{\mathrm{3}}} \\ $$$$\mathrm{2}\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\pi}{\sqrt{\mathrm{3}}}\:\Rightarrow\bigstar\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\bigstar \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 14/May/20

sorry 2 ∫_0 ^∞ (dx/(x^4 +x^2 +1)) =(π/(√3)) ⇒★ ∫_0 ^∞ (dx/(x^4 +x^2 +1)) =(π/(2(√3))) ★

$${sorry}\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\pi}{\sqrt{\mathrm{3}}}\:\Rightarrow\bigstar\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:\bigstar \\ $$

Answered by Kunal12588 last updated on 14/May/20

(x^4 +x^2 +1)=(ax^2 +bx+c)(px^2 +qx+r) x^4 +x^2 +1=apx^4 +(aq+bp)x^3 +(ar+bq+cp)x^2 +(br+cq)x+cr a=1, b=±1, c=1 p=1, q=∓1, r=1 x^4 +x^2 +1=(x^2 +x+1)(x^2 −x+1) (1/(x^4 +x^2 +1))=((ax+b)/(x^2 +x+1))+((px+q)/(x^2 −x+1)) 1=(a+p)x^3 +(−a+b+p+q)x^2 +(a−b+p+q)x +(b+q) a=(1/2), b=(1/2) p=((−1)/2), q=(1/2) (1/(x^4 +x^2 +1))=((x+1)/(x^2 +x+1))−((x−1)/(x^4 +x+1)) I=∫(dx/(x^4 +x^2 +1))=(1/2)∫((x+1)/(x^2 +x+1))dx−(1/2)∫((x−1)/(x^2 +x+1))dx I_1 =(1/2)∫((x+1)/(x^2 +x+1))dx =(1/4)∫((2x+1)/(x^2 +x+1))dx+(1/4)∫(dx/(x^2 +x+1)) =(1/4)ln∣x^2 +x+1∣+(1/4)∫(dx/((x+(1/2))^2 +(3/4))) =(1/4)ln∣x^2 +x+1∣+(1/4)×(2/(√3)) tan^(−1) (((x+(1/2)))/((√3)/2))+c I_1 =(1/4)ln∣x^2 +x+1∣+(1/(2(√3))) tan^(−1) ((2x+1)/(√3))+m I_2 =(1/2)∫((x−1)/(x^2 −x+1))dx =(1/4)∫((2x−1)/(x^2 −x+1))dx−(1/4)∫(dx/(x^2 −x+1)) =(1/4)ln∣x^2 −x+1∣−(1/4)∫(dx/((x−(1/2))^2 +(((√3)/2))^2 )) I_2 =(1/4)ln∣x^2 −x+1∣−(1/(2(√3)))tan^(−1) ((2x−1)/(√3))+n I=(1/4)ln∣x^2 +x+1∣+(1/(2(√3))) tan^(−1) ((2x+1)/(√3)) −(1/4)ln∣x^2 −x+1∣+(1/(2(√3)))tan^(−1) ((2x−1)/(√3))+C =(1/4)ln∣((x^2 +x+1)/(x^2 −x+1))∣+(1/(2(√3)))[tan^(−1) ((2x+1)/(√3))+tan^(−1) ((2x−1)/(√3))]+C ∫_0 ^∞ (dx/(x^4 +x^2 +1))=(1/4)[ln∣((x^2 +x+1)/(x^2 −x+1))∣]_0 ^∞ + +(1/(2(√3)))[tan^(−1) ((2x+1)/(√3))+tan^(−1) ((2x−1)/(√3))]_0 ^∞ =(1/4){ln(((1+(1/∞)+(1/∞^2 ))/(1−(1/∞)+(1/∞^2 ))))−ln(((0^2 +0+1)/(0^2 −0+1)))} +(1/(2(√3))){tan^(−1) (∞)+tan^(−1) (∞)−tan^(−1) ((1/(√3)))−tan^(−1) (((−1)/(√3)))} =(1/4)[ln(1)−ln(1)]+(1/(2(√3)))[(π/2)+(π/2)−(π/6)+(π/6)] =(π/(2(√3))) ∫_0 ^∞ (dx/(x^4 +x^2 +1))=(π/(2(√3)))

$$\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)=\left({ax}^{\mathrm{2}} +{bx}+{c}\right)\left({px}^{\mathrm{2}} +{qx}+{r}\right) \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}={apx}^{\mathrm{4}} +\left({aq}+{bp}\right){x}^{\mathrm{3}} +\left({ar}+{bq}+{cp}\right){x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({br}+{cq}\right){x}+{cr} \\ $$$${a}=\mathrm{1},\:{b}=\pm\mathrm{1},\:{c}=\mathrm{1} \\ $$$${p}=\mathrm{1},\:{q}=\mp\mathrm{1},\:{r}=\mathrm{1} \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}=\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$ \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{{ax}+{b}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\frac{{px}+{q}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\mathrm{1}=\left({a}+{p}\right){x}^{\mathrm{3}} +\left(−{a}+{b}+{p}+{q}\right){x}^{\mathrm{2}} +\left({a}−{b}+{p}+{q}\right){x} \\ $$$$\:\:\:\:\:\:\:\:+\left({b}+{q}\right) \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}},\:{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}=\frac{−\mathrm{1}}{\mathrm{2}},\:{q}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}−\frac{{x}−\mathrm{1}}{{x}^{\mathrm{4}} +{x}+\mathrm{1}} \\ $$$$ \\ $$$${I}=\int\frac{{dx}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:{tan}^{−\mathrm{1}} \frac{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}+{c} \\ $$$$ \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}+{m} \\ $$$$ \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}+{n} \\ $$$$ \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}+{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right]+{C} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\infty} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\sqrt{\mathrm{3}}}+{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\infty}+\frac{\mathrm{1}}{\infty^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{1}}{\infty}+\frac{\mathrm{1}}{\infty^{\mathrm{2}} }}\right)−{ln}\left(\frac{\mathrm{0}^{\mathrm{2}} +\mathrm{0}+\mathrm{1}}{\mathrm{0}^{\mathrm{2}} −\mathrm{0}+\mathrm{1}}\right)\right\} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left\{{tan}^{−\mathrm{1}} \left(\infty\right)+{tan}^{−\mathrm{1}} \left(\infty\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)−{tan}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\left(\mathrm{1}\right)−{ln}\left(\mathrm{1}\right)\right]+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{6}}\right] \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$

Commented by niroj last updated on 14/May/20

Great hardwork����

Commented by prakash jain last updated on 14/May/20

������

Commented by Kunal12588 last updated on 14/May/20

thanks sir!

Commented by mathmax by abdo last updated on 14/May/20

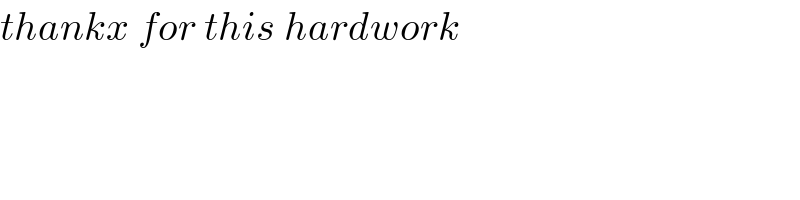
thankx for this hardwork

$${thankx}\:{for}\:{this}\:{hardwork} \\ $$

Answered by Ar Brandon last updated on 14/May/20

L=∫_0 ^∞ (dx/(x^4 +x^2 +1))=(1/2)∫_0 ^∞ (((x^2 +1)−(x^2 −1))/(x^4 +x^2 +1))dx ⇒2L=∫_0 ^∞ ((x^2 +1)/(x^4 +x^2 +1))dx−∫_0 ^∞ ((x^2 −1)/(x^4 +x^2 +1))dx ⇒2L=∫_0 ^∞ ((1+(1/x^2 ))/(x^2 +1+(1/x^2 )))dx−∫_0 ^∞ ((1−(1/x^2 ))/(x^2 +1+(1/x^2 )))dx ⇒2L=∫_0 ^∞ ((1+(1/x^2 ))/((x−(1/x))^2 +3))dx−∫_0 ^∞ ((1−(1/x^2 ))/((x+(1/x))^2 −1))dx ⇒2L=_(u=x−(1/x)) ^(v=x+(1/x)) ∫_(−∞) ^(+∞) (du/(u^2 +3))−∫_(+∞) ^(+∞) (dv/(v^2 −1)) 2L=((√3)/3)[arctan((u/(√3)))]_(−∞) ^(+∞) 2L=((π(√3))/3)⇒L=((π(√3))/6) ∫_0 ^∞ (dx/(x^4 +x^2 +1))=((π(√3))/6)

$$\mathrm{L}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{d}{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)−\left({x}^{\mathrm{2}} −\mathrm{1}\right)}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{2L}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{x}−\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{2L}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\mathrm{d}{x}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{2L}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}\mathrm{d}{x}−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}}\mathrm{d}{x} \\ $$$$\Rightarrow\mathrm{2L}\underset{\mathrm{u}={x}−\frac{\mathrm{1}}{{x}}} {\overset{\mathrm{v}={x}+\frac{\mathrm{1}}{{x}}} {=}}\int_{−\infty} ^{+\infty} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{3}}−\int_{+\infty} ^{+\infty} \frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{2L}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left[\mathrm{arctan}\left(\frac{\mathrm{u}}{\sqrt{\mathrm{3}}}\right)\right]_{−\infty} ^{+\infty} \\ $$$$\mathrm{2L}=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}}\Rightarrow\mathrm{L}=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{d}{x}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com