Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 69607 by malwaan last updated on 25/Sep/19

without using lhospital please prove that lim_(x→0) ((x−sin x)/x^3 ) = (1/6) I want every method possible because someone challenge me

$$\boldsymbol{{without}}\:\boldsymbol{{using}}\:\boldsymbol{{lhospital}}\:\boldsymbol{{please}} \\ $$$$\boldsymbol{{prove}}\:\boldsymbol{{that}} \\ $$$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\:\frac{\boldsymbol{{x}}−\boldsymbol{{sin}}\:\boldsymbol{{x}}}{\boldsymbol{{x}}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{want}}\:\boldsymbol{{every}}\:\boldsymbol{{method}} \\ $$$$\boldsymbol{{possible}}\:\boldsymbol{{because}}\:\boldsymbol{{someone}} \\ $$$$\boldsymbol{{challenge}}\:\boldsymbol{{me}}\: \\ $$

Commented by mathmax by abdo last updated on 26/Sep/19

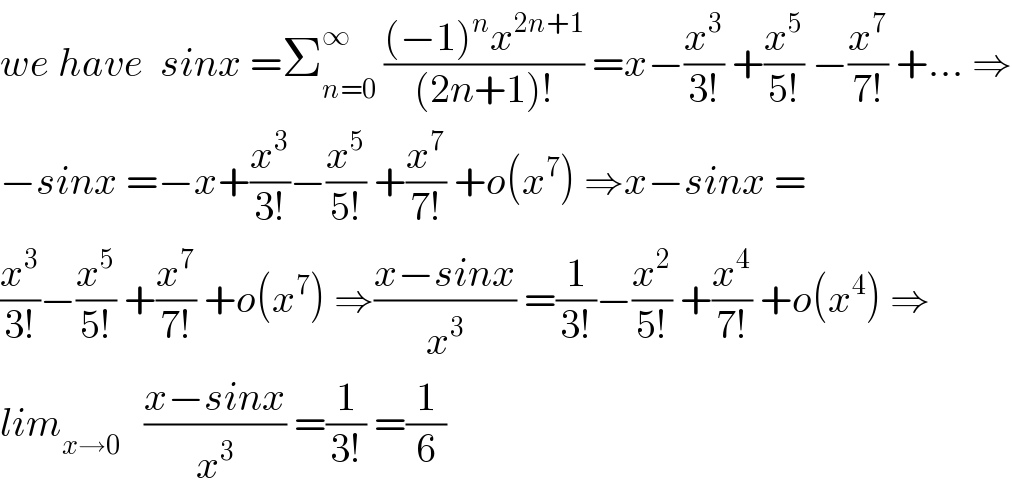
we have sinx =Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) =x−(x^3 /(3!)) +(x^5 /(5!)) −(x^7 /(7!)) +... ⇒ −sinx =−x+(x^3 /(3!))−(x^5 /(5!)) +(x^7 /(7!)) +o(x^7 ) ⇒x−sinx = (x^3 /(3!))−(x^5 /(5!)) +(x^7 /(7!)) +o(x^7 ) ⇒((x−sinx)/x^3 ) =(1/(3!))−(x^2 /(5!)) +(x^4 /(7!)) +o(x^4 ) ⇒ lim_(x→0) ((x−sinx)/x^3 ) =(1/(3!)) =(1/6)

$${we}\:{have}\:\:{sinx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\:−\frac{{x}^{\mathrm{7}} }{\mathrm{7}!}\:+...\:\Rightarrow \\ $$$$−{sinx}\:=−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\:+\frac{{x}^{\mathrm{7}} }{\mathrm{7}!}\:+{o}\left({x}^{\mathrm{7}} \right)\:\Rightarrow{x}−{sinx}\:= \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\:+\frac{{x}^{\mathrm{7}} }{\mathrm{7}!}\:+{o}\left({x}^{\mathrm{7}} \right)\:\Rightarrow\frac{{x}−{sinx}}{{x}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{3}!}−\frac{{x}^{\mathrm{2}} }{\mathrm{5}!}\:+\frac{{x}^{\mathrm{4}} }{\mathrm{7}!}\:+{o}\left({x}^{\mathrm{4}} \right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{x}−{sinx}}{{x}^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{3}!}\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by Prithwish sen last updated on 25/Sep/19

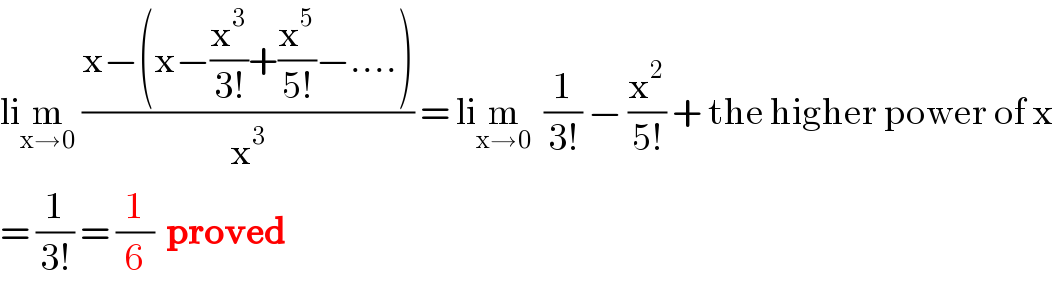
lim_(x→0) ((x−(x−(x^3 /(3!))+(x^5 /(5!))−....))/x^3 ) = lim_(x→0) (1/(3!)) − (x^2 /(5!)) + the higher power of x = (1/(3!)) = (1/6) proved

$$\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\:\frac{\mathrm{x}−\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{5}!}−....\right)}{\mathrm{x}^{\mathrm{3}} }\:=\:\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\:\:\frac{\mathrm{1}}{\mathrm{3}!}\:−\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{5}!}\:+\:\mathrm{the}\:\mathrm{higher}\:\mathrm{power}\:\mathrm{of}\:\mathrm{x} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}!}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\:\:\boldsymbol{\mathrm{proved}} \\ $$

Commented by malwaan last updated on 26/Sep/19

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by malwaan last updated on 27/Sep/19

thank you so much

$${thank}\:{you}\:{so}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com